本文的閱讀等級:高級
美國作家梭羅 (Henry D. Thoreau) 在《湖濱散記》談到他的幽居生活時,說道[1]:
我們的生活消耗在瑣碎之中。一個老實的人除了十指之外,便不必有更大的數字了,頂多加上十個足趾,其餘不妨勉強一下。簡單,簡單,簡單啊!我說,最好你的事祇兩三件,不要一百件或一千件;不必一百萬一百萬地計算,半打不夠計算嗎?總之,賬目可以記在大拇指甲上就好了。
我們也許不能複製梭羅在瓦爾登湖 (Walden) 的簡單生活,但是我們永遠可以通過化繁為簡來改善現況。處於資訊爆炸的時代,我們不免要面對變數很多且樣本數很大的資料。在分析高維度 (變數很多) 數據時,降維 (dimension reduction) 常是一個必要的前處理工作。主成分分析 (principal components analysis,簡稱 PCA) 由英國統計學家皮爾生 (Karl Pearson) 於1901年提出[2],是一種降低數據維度的有效技術。主成分分析的主要構想是分析共變異數矩陣 (covariance matrix) 的特徵性質 (見“共變異數矩陣與常態分布”),以得出數據的主成分 (即特徵向量) 與它們的權值 (即特徵值);透過保留低階主成分 (對應大特徵值),捨棄高階主成分 (對應小特徵值),達到減少數據集維度,同時保留最大數據集變異的目的。本文從線性代數觀點介紹主成分分析,並討論實際應用時可能遭遇的一些問題。
假設我們有一筆維數等於 ,樣本大小是
的數據
,即每一數據點
包含
個變數的量測值。如果我們想要以單一向量
來代表整組數據,可用均方誤差作為誤差函數:
。
上式中,誤差平方和除以 而非
的緣由請見“樣本平均數、變異數和共變異數”。理想的中心向量
必須有最小的均方誤差,滿足此條件的向量是
,
稱為樣本平均數向量。證明如下:
根據樣本平均數向量 的表達式,上式最後一項等於零。因為
,可知
,等號於
時成立。
數據點 與其分布平均的差,
,稱為離差 (deviation)。在變數數目
很大時,如何「目視」離差的散布情況?最簡單的作法是降維,譬如,將散布於高維空間
的離差「壓縮」至一直線上。令直線
穿越
,
為其指向向量,且
。直線
上的任一點可表示如下:
,
其中 為一純量,
代表
至
的距離。一旦
給定,我們可以用
來近似
,也就是以
近似離差
。如同樣本平均數向量的設定方式,最佳的近似係數
必須最小化均方誤差:
因為 ,計算偏導數
並設為零,
。
由此解得
。
從幾何觀點解釋, 即是離差
在直線
的正交投影,以下稱為正交原則 (見圖1,參閱“正交投影──威力強大的線代工具”)。
接下來我們尋找使 最小化的直線方向
。將先前解出的最佳係數代回
,整理可得
上面使用了 。令
,
稱為樣本共變異數矩陣。乘開上式,確認 的
元
即為第
個變數和第
個變數的樣本共變異數:
,
其中 是第
個數據點的第
個變數 (即
的第
元),
是第
個變數的樣本平均數 (即
的第
元)。明顯地,
,故
是一
階對稱矩陣。對於任一
維向量
,
,
即知 是半正定矩陣。數據集的總變異量 (即離差平方和)
是一常數,所以最小化
等價於最大化
。我們的問題變成求解下列約束二次型:
。
解法如下 (另一個解法見“Hermitian 矩陣特徵值的變化界定”)。使用 Lagrange 乘數法 (見“Lagrange 乘數法”),定義
,
其中 是未定的 Lagrange 乘數。計算偏導數 (即梯度) 並設為零,
,
可得
。
直線 的指向向量
就是樣本共變異數矩陣
的特徵向量。因為
,欲使
有最大值,我們必須選擇對應最大特徵值的特徵向量。實對稱半正定矩陣有非負的特徵值 (見“半正定矩陣的判別方法”),故可設
的特徵值為
。此外,
的特徵向量構成一個單範正交集 (orthonormal set),見“實對稱矩陣可正交對角化的證明”,這個性質將於稍後使用。我們選擇對應最大特徵值
的特徵向量作為
,透過離差
在直線
的正交投影
即可粗估數據集的散布情況。
如果我們想獲得較為精確的近似結果,以上過程可推廣至更高維度。考慮
,
其中 。我們的目標是尋找一組單範正交集
,即
(稱為 Kronecker 記號,
若
,否則
),使最小化
。
根據正交原則,組合係數 就是離差
至單位向量
的正交投影量,即
。重複前述推導方式,可以證明[3]
。
緊接的任務要解出約束二次型:
。
仍然使用 Lagrange 乘數法,定義
,
其中 是未定的 Lagrange 乘數。計算偏導數,並設結果為零向量:
。
對於 ,設
,則
。
換句話說,當 是樣本共變數矩陣
的最大
個特徵值
的對應 (單範正交) 特徵向量時,目標函數
有最大值。當然,這並不是唯一解,但可以證明所有的解都有相同的目標函數值
[4]。不過,如果要求
滿足
,
,則樣本共變數矩陣
的特徵向量集是唯一的選擇[5]。
我們以 近似數據點
,樣本共變異數矩陣
的特徵向量
描述了數據集的主要成分,因此稱為主成分。那麼
的特徵值又有甚麼涵義呢?特徵值
就是主成分
的係數
(稱為主成分係數) 的變異數。首先證明
的平均數是零:對於
,
。
再來計算 的樣本變異數:
所以說,特徵值 表示主成分
的權值。另外必須一提的是,主成分係數
和
沒有相關性,即樣本共變異數
為零。當
,
給定維度等於 的數據集
,主成分分析的計算程序與結果可整理成簡明的矩陣形式。
- 計算樣本平均
,定義
階離差矩陣
,
階樣本共變異數矩陣則是
。
- 將
正交對角化為
,
其中
是特徵值矩陣,
代表主成分的權值,
是單範正交特徵向量構成的
階正交主成分矩陣,
。圖2顯示
的資料散布圖,樣本平均數向量
,以及主成分
和
。圖中橢圓的長軸平方與短軸平方之比等於主成分係數
的變異數與
的變異數之比,即
。
- 定義
階主成分係數矩陣
,其中
,因此
。
上式等號兩邊右乘
,可得
。換一個說法,數據點
的主成分分解式為
。
主成分係數
是離差
參考單範正交基底
的座標向量。
最後還有一些與實際應用面相關的細節需要釐清。
- 我們應當保留多少低階主成分 (對應大特徵值的特徵向量)?也就是說,如何選擇
?常用的一種方式是設定近似數據
的變異與原始數據
的變異的比例。譬如,選擇最小的
使得
,
表示我們保留了 80% 的數據變異。
- 若數據的變數具有不同的變異,主成分方向會受到變異大的變數所決定。如欲排除這個影響,我們可以用樣本相關矩陣取代樣本共變異數矩陣。在套用主成分分析之前,預先將每一變數予以標準化 (standardized),如下:
其中
是第
個變數的樣本變異數,即
。標準化後的數據集的樣本共變異數矩陣即為樣本相關矩陣
。
請讀者自行驗證
的
元就是第
個變數與第
個變數的相關係數 (見“相關係數”)。這時候,數據集的總變異等於維數
,原因如下:
。
上面使用了跡數循環不變性
(見“跡數的性質與應用”),最後一個等式係因
的主對角元皆為
。
- 如何得到數值穩定的主成分
,權值
,以及主成分係數
,
,
?答案是奇異值分解 (singular value decomposition)。通過主成分分析與奇異值分解的關係可以顯現主成分分析隱含的其他訊息 (見“主成分分析與奇異值分解”)。
註解
[1] Henry D. Thoreau 的 Walden,原文如下:“Our life is frittered away by detail. An honest man has hardly need to count more than his ten fingers, or in extreme cases he may add his ten toes, and lump the rest. Simplicity, simplicity, simplicity! I say, let your affairs be as two or three, and not a hundred or a thousand; instead of a million count half a dozen, and keep your accounts on your thumb-nail.” 中譯取自《湖濱散記》,吳明實譯,今日世界出版社,1978年,83頁。
[2] 維基百科:主成分分析
[3]
[4] 考慮
。
令 且
。
將條件方程組寫成矩陣形式:
。
因為 有單範正交行向量,
。上式左乘
,即有
。下面證明滿足條件式的任何解
和
都有相同的目標函數值:
。
將實對稱矩陣 正交對角化為
,其中
是一正交矩陣,
,
。條件式
左乘
,右乘
,可得
,
上面我們令 。因為
,
也有單範正交行向量,故知
和
也是一組解。利用跡數循環不變性,
,
證明 和
所含的兩組單範正交集有相同的目標函數值
。
[5] 假設我們已經求得最大化 的單位向量
,滿足
。下一步要找出單位向量
使最大化
,並滿足
。寫出
,
其中 是 Lagrange 乘數。計算偏導數,設結果為零:
。
上式左乘 ,可得
。另一方面,
。所以,
,即得
。明顯地,我們選擇
,
是對應的單位特徵向量。同樣的推導步驟可以推廣至
的情況。



最近又去聽了微積分的課,剛好聽到了講述simpison數值積分方法。數值積分方法特別可以處理非平滑的函數數據。其中可達到一定精確度的simpison方法,用了拋物線來近似分散的數據,其手法就是揉合上述的正交投影以及黎曼和的概念。因為正交投影,所以可以控制誤差到一定範圍內,黎曼積分也就可以派上用場。只是我好奇的是,因為訊號處理常常用到傅立葉分析來搜尋出有用的訊號,那麼是否可以用傅立葉分析來做數值積分呢?
Simpson 積分法則的原理是Newton-Cotes公式: ,
, ,
, 。通常我們使用一內插多項式來近似
。通常我們使用一內插多項式來近似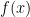 以得到
以得到 的計算公式。這個式子看起來很像是Hilbert空間的函數近似問題:最小化
的計算公式。這個式子看起來很像是Hilbert空間的函數近似問題:最小化 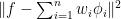 ,
,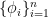 是我們喜愛的基底,最佳近似確實是
是我們喜愛的基底,最佳近似確實是 在這個基底所擴張的子空間的正交投影。
在這個基底所擴張的子空間的正交投影。
傅立葉變換是一種積分變換,它可以用來計算函數近似的三角級數(trigonometric series),或證明一些定理,但我不知道是否亦可作數值積分用。
傅立葉積分轉換是把時域的資訊轉換成頻率域的資訊,你可以理解成他把時域中某個頻率的能量積分然後放到頻率域中去。所以沒錯,傅立葉轉換本身是有積分的效果在的,只是他把要拿來積分的東西分離成正交的獨立函數分別處理。
https://zh.wikipedia.org/wiki/%E8%B0%B1%E5%AF%86%E5%BA%A6
https://zh.wikipedia.org/wiki/%E5%B8%95%E5%A1%9E%E7%93%A6%E5%B0%94%E5%AE%9A%E7%90%86
請問主成分分析是否一定要進行標準化?
如果變數的尺規(scale)相似,譬如,全部都是EEG訊號,那麼使用共變異數矩陣即可。如果變數的尺規差異很大,譬如,年所得,年齡,體重,那麼應該使用相關係數矩陣(即標準化後的共變異數矩陣)。
周老師,我有兩個問題:
1)對E1求ck的偏導數是否第一個2前面的負號應該去掉?
2)對L({Wj},{u[i,j]})求偏導後,為什麼可以假設u[i,j]+u[j,i]=0從而將wj消去?
謝謝指正。
你可以試一下 的例子,未知數有4個:
的例子,未知數有4個: 。
。

 和
和 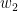 不為零向量),故
不為零向量),故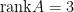 ,也就是說有無限多組解,故可設
,也就是說有無限多組解,故可設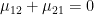 。同理,對於
。同理,對於 個未知數
個未知數  ,
,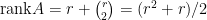 ,即有
,即有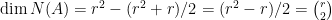 。所以我們可以放心地設
。所以我們可以放心地設 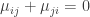 ,
,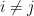 。
。
線性方程組為
係數矩陣A只有三個線性獨立的行向量(因為
突然想起在高中生時,我的數學老師常告誡我要將算式寫清楚。
老師,我還是有一些不明白。我自己推導一次後覺得u[i,j]+u[j,i]=0是必然發生的事,為什麼老師您要“設”呢?
啊,真的嗎?你有空時方便將過程貼上網或寄給我看看嗎?
左乘 ,
,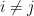 ,可得
,可得
上式不能推斷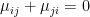 ,雖然
,雖然  ,但
,但 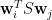 未必等於零。
未必等於零。
我說“推導”有些誇張了,其實我就寫了幾個步驟然後直覺地覺得,u[i,j]和u[j,i](i not equal to j)所對應的在A中的行向量必然一樣,所以所有形如
c * [0 0 … 1 … -1 0 …]’ 必然在A的零空間中,其中c為某一非零實數,1位於u[i,j]的位置,-1位於u[j,i]的位置。所有這些互為正交向量構成了A的零空間的基底,因此所有齊次解滿足u[i,j]+u[j,i]=0 if i is not equal to j。要令方程組成立,[Sw[1],…Sw[r]]’必須在X=span{W[1],…,w[r]}中,也就是說X是S的不變子空間。後來發現在推導的時候想當然地認為X就是S的特徵空間(eigenspace)所以必然有Sw[k]=lamda*w[k]從而得到方程組的特解中也必須有u[i,j]+u[j,i]=0 if i is not equal to j這個結論。我曾嘗試過證明X是滿足所有條件的唯一不變子空間但失敗了。
老師,不知道為什麼,我對這個假設沒有“安全感”,萬一該假設不成立那麼之後的證明就只有或然性而不是必然性了。
我明白了。沒有安全感是好事。朱熹說:「讀書,始讀未知有疑。其次則漸漸有疑,中則節節是疑。過了這一番后,疑漸漸解,以至融會貫通,都無所疑,方始是學。」
謝謝老師。
我們可以從另一個角度切入:根據註解二,待解的方程式為 ,
,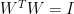 。因為
。因為  ,故可正交對角化為
,故可正交對角化為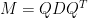 ,其中
,其中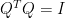 ,
,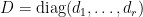 。代入可得
。代入可得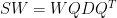 ,右乘
,右乘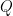 ,
,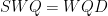 。令
。令 ,
, 。問題變成
。問題變成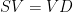 ,也就是
,也就是 ,
, 。
。
W^T=W經過老師一點明果然豁然開朗。另外,老師的意思是因為M^T=M所以M可正交對角話吧。
非常感謝老師。
周老師,請問一下主成份分析和主成份回歸的關係為何?主成份回歸是否只是主成份分析的一個應用而已?
PCR (principal components regression) 就是 PCA+multiple regression。俗話說:蟑螂怕拖鞋,烏龜怕鐵鎚。在資料分析,線性模型怕共線性(collinearity),非線性模型怕過度擬合(over-fitting)。如果數據輸入矩陣X的維數很大(變數很多)且變數之間相關,則multiple regression的估計係數的變異很大(表示模型不可信賴)。為了解決這個問題,先對X進行主成分分析,取得低維數的主成分係數矩陣Z(各變數無關),透過適當的變數選擇方法(譬如計算輸出y和z_i的相關係數)挑選出一部分的z變數當作新的數據輸入,然後建模,再將估計出的z_i係數轉換回變數x_j的係數,此法稱為PCR estimator。詳見
http://en.wikipedia.org/wiki/Principal_component_regression
周老師 您好:
https://stats.stackexchange.com/questions/66926/what-are-the-four-axes-on-pca-biplot
目前資料分析使用主成分分析方法通常會畫一張叫做 biplot的圖來看看各筆資料在第一集第二主成分所組成的平面上到底比較受到哪一個原始參數的影響,在上述網頁中有提到這張圖到底是怎麼畫的,但是為什麼在biplot中的紅色箭頭向量並非只是主成分中各個變數佔的比例,而是還得乘上(主成分的解釋變異*資料筆數^(1/2))?
請參考
裡面的factor loading matrix
周老師,注釋3最後一個式子的第一項應該有個n-1的系數
非常謝謝,已訂正。