本文的閱讀等級:初級
對於一 階實矩陣
,行空間 (column space)
乃
的行向量於
中擴張而成的子空間:
零空間 (nullspace) 則是齊次方程
所有解形成的一個屬於
的子空間:
在一般情況下,矩陣行空間採用明確的 (explicit) 建構式 (即擴張) 定義,而零空間則以隱含的 (implicit) 限制條件 (即線性方程組) 來定義。本文探討如何運用簡約列梯形式 (reduced row echelon form) 解決下面兩個子空間互換表達問題:給定 ,將零空間
表示成明確的向量集擴張,也就是說,求矩陣
使得
;另一方面,行空間
也可以表示為隱含的限制條件,亦即求矩陣
使得
。
考慮下面的 階矩陣
運用高斯消去法化簡 得到簡約列梯形式:
消去法所執行的基本列運算不改變方程式的解,故 等價於
,亦即
和
有相同的零空間。觀察得知
所對應的齊次方程式為
我們稱等號左邊的 ,
,
為軸變數,等號右邊的
和
為自由變數。每個軸變數都被一個方程式鎖定,自由變數則不受方程式控制,故可設
,
,齊次方程
的完整解則表示為兩個特解的線性組合:
也就是說,。由於每一特解對應一自由變數,所有特解構成一線性獨立集。將
和
合併為一矩陣:
因此 ,
的零空間即為
的行空間,
,我們稱
是
的零空間矩陣 (nullspace matrix)。由簡約列梯形式
可以得到以下訊息:列數即方程式的總數 (
),行數即變數個數 (
),軸變數個數 (
),和自由變數個數 (
),即知
為一
階矩陣。矩陣
的「表面尺寸」由其列數
和行數
決定,但其「真實尺寸」則由軸數
決定,因為每個軸列對應一個實際有效的式子,從而鎖定該軸行所對應的變數。所以我們定義矩陣秩
為軸的總數,亦即軸列、軸行的個數 (見“你不能不知道的矩陣秩”)。
以上零空間矩陣 的推導過程還可以加以簡化。若不考慮
的零列與
的自由變數列,
的非軸行 (即第
,
行) 恰好對應
的兩個行,惟其正負符號相反。令
的軸行置於最左邊,
對應自由變數的列置於最底下,就有以下分塊矩陣形式:
其中 是
階分塊。矩陣
的每一行都屬於
的零空間,就有
直接計算分塊矩陣乘法也可以得到同樣的結果,
以分塊形式表現簡約列梯形式的好處是不需要經過解齊次方程 過程,直接從
的形式立即可推得零空間矩陣
。
這裡補充 的證明。因為任一
維向量
使得
,可知
。另一方面,假設
,即
。寫出
,其中
與
分別是
維與
維向量,則
,
即得 。所以,
,證明
。
最後我們回答第二個問題:給定矩陣 ,如何得到
使得
?根據正交補餘關係
(見“線性代數基本定理(二)”),解出
矩陣的關鍵在於
的零空間矩陣,設為
,就有
。再利用
,可得
上式表明所求矩陣即為 。另一個想法直接從
下手,取轉置即得
,問題因此轉換為計算
的零空間矩陣
。考慮上例矩陣
,將
化簡成簡約列梯形式:
即知 的零空間矩陣:
也就得到
欲使 有解,
必須在
的行空間,換句話說,
滿足
因為零空間矩陣 有獨立行向量,可知
階
矩陣有線性獨立的列向量,故
。另外,
,由秩—零度定理
, 即得
。

解第二个问题的过程中,在得出A的转置的最简阶梯型后,一眼便可看出其零空间矩阵,这对于人来说没什么问题,但是如果要用某个算式来表达从最简阶梯型矩阵取出零空间矩阵的话,这个算式是什么呢?想了很久很久没有结果,只好向老师请教一下,多谢指教啊
從最簡階梯型矩陣取出零空間矩陣(可能)不存在你想要的算式(formula),但是有算法(algorithm),見本文的相關閱讀:零空間的快捷算法
請問老師:

X 是 ,可是
,可是

 ,有差別嗎?
,有差別嗎?
可以使
請檢查計算結果。
原來,

如果, ,則
,則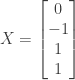 嗎??
嗎??
此例 有2個軸元,表示
有2個軸元,表示  的解集合(即
的解集合(即 的零空間)的維數等於4-2=2。使用下文的算法:
的零空間)的維數等於4-2=2。使用下文的算法:
可得基解
請問老師:

這不是簡約列梯型式嗎?
不是的,簡約列梯型式的定義請見
謝謝,
條件為
軸元為 1;
軸元其上方和下方的元皆為零。這個條件不符。