網友Rich留言：
哈囉周老師你好。想請教一個問題：eigenvalue and eigenvector 所代表的物理意義是什麼？謝謝。
答曰：
假設 
若 
其中 
設想我們被指派擔任矩陣設計工作，第一個任務是設計對X-軸鏡射 (反射，reflection) 的變換矩陣。對於 
![\displaystyle T\left(\begin{bmatrix} x_1\\ x_2 \end{bmatrix}\right)=\left[\!\!\begin{array}{r} x_1\\ -x_2 \end{array}\!\!\right]=x_1\begin{bmatrix} 1\\ 0 \end{bmatrix}+x_2\left[\!\!\begin{array}{r} 0\\ -1 \end{array}\!\!\right]=\left[\!\!\begin{array}{cr} 1&0\\ 0&-1 \end{array}\!\!\right]\begin{bmatrix} x_1\\ x_2 \end{bmatrix}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++T%5Cleft%28%5Cbegin%7Bbmatrix%7D++x_1%5C%5C++x_2++%5Cend%7Bbmatrix%7D%5Cright%29%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Br%7D++x_1%5C%5C++-x_2++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%3Dx_1%5Cbegin%7Bbmatrix%7D++1%5C%5C++0++%5Cend%7Bbmatrix%7D%2Bx_2%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Br%7D++0%5C%5C++-1++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++1%260%5C%5C++0%26-1++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%5Cbegin%7Bbmatrix%7D++x_1%5C%5C++x_2++%5Cend%7Bbmatrix%7D&bg=ffffff&fg=000000&s=0&c=20201002)
上式裡的對角矩陣即為所求。令
![D=\left[\!\!\begin{array}{cr} 1&0\\ 0&-1 \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++1%260%5C%5C++0%26-1++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
往後我們稱 
對直線 L 的鏡射
直線
注意上面兩式具有相同型態，即
數學家稱純量 
線性算子 
若一個鏡射算子 
![\mathbf{v}_2=\left[\!\!\begin{array}{r} -1\\ 2 \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7Bv%7D_2%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Br%7D++-1%5C%5C++2++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
其中組合係數 
![[\mathbf{x}]_{\boldsymbol{\beta}}=\begin{bmatrix} c_1\\ c_2 \end{bmatrix}](https://s0.wp.com/latex.php?latex=%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D%3D%5Cbegin%7Bbmatrix%7D++c_1%5C%5C++c_2++%5Cend%7Bbmatrix%7D&bg=ffffff&fg=000000&s=0&c=20201002)
再寫出 
![[T(\mathbf{x})]_{\boldsymbol{\beta}}=\left[\!\!\begin{array}{r} c_1\\ -c_2 \end{array}\!\!\right]=\left[\!\!\begin{array}{cr} 1&0\\ 0&-1 \end{array}\!\!\right]\begin{bmatrix} c_1\\ c_2 \end{bmatrix}=D[\mathbf{x}]_{\boldsymbol{\beta}}](https://s0.wp.com/latex.php?latex=%5BT%28%5Cmathbf%7Bx%7D%29%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Br%7D++c_1%5C%5C++-c_2++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++1%260%5C%5C++0%26-1++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%5Cbegin%7Bbmatrix%7D++c_1%5C%5C++c_2++%5Cend%7Bbmatrix%7D%3DD%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
我們得到一個令人震驚的結果：若參考特徵向量構成的基底，所有的鏡射矩陣必可轉換成標準鏡射矩陣
![\mathbf{x}=c_1\mathbf{v}_1+c_2\mathbf{v}_2=\begin{bmatrix} \mathbf{v}_1&\mathbf{v}_2 \end{bmatrix}\begin{bmatrix} c_1\\ c_2 \end{bmatrix}=S[\mathbf{x}]_{\boldsymbol{\beta}}](https://s0.wp.com/latex.php?latex=%5Cmathbf%7Bx%7D%3Dc_1%5Cmathbf%7Bv%7D_1%2Bc_2%5Cmathbf%7Bv%7D_2%3D%5Cbegin%7Bbmatrix%7D++%5Cmathbf%7Bv%7D_1%26%5Cmathbf%7Bv%7D_2++%5Cend%7Bbmatrix%7D%5Cbegin%7Bbmatrix%7D++c_1%5C%5C++c_2++%5Cend%7Bbmatrix%7D%3DS%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
其中 ![S=\begin{bmatrix} \mathbf{v}_1&\mathbf{v}_2 \end{bmatrix}=\left[\!\!\begin{array}{cr} 2&-1\\ 1&2 \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=S%3D%5Cbegin%7Bbmatrix%7D++%5Cmathbf%7Bv%7D_1%26%5Cmathbf%7Bv%7D_2++%5Cend%7Bbmatrix%7D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++2%26-1%5C%5C++1%262++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
![[\mathbf{x}]_{\boldsymbol{\beta}}=S^{-1}\mathbf{x}](https://s0.wp.com/latex.php?latex=%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D%3DS%5E%7B-1%7D%5Cmathbf%7Bx%7D&bg=ffffff&fg=000000&s=0&c=20201002)
![[T(\mathbf{x})]_{\boldsymbol{\beta}}=S^{-1}T(\mathbf{x})](https://s0.wp.com/latex.php?latex=%5BT%28%5Cmathbf%7Bx%7D%29%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D%3DS%5E%7B-1%7DT%28%5Cmathbf%7Bx%7D%29&bg=ffffff&fg=000000&s=0&c=20201002)
或圖示如下：
故
![\displaystyle A=SDS^{-1}=\left[\!\!\begin{array}{cr} 2&-1\\ 1&2 \end{array}\!\!\right]\left[\!\!\begin{array}{cr} 1&0\\ 0&-1 \end{array}\!\!\right]\frac{1}{5}\left[\!\!\begin{array}{rc} 2&1\\ -1&2 \end{array}\!\!\right]=\frac{1}{5}\left[\!\!\begin{array}{cr} 3&4\\ 4&-3 \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++A%3DSDS%5E%7B-1%7D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++2%26-1%5C%5C++1%262++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++1%260%5C%5C++0%26-1++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%5Cfrac%7B1%7D%7B5%7D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Brc%7D++2%261%5C%5C++-1%262++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%3D%5Cfrac%7B1%7D%7B5%7D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++3%264%5C%5C++4%26-3++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
給定一個變換矩陣 
線代啟示錄 
我整理了一些常見的矩陣特徵值與特徵向量，加入專題探究分頁：
真實的特徵向量物理意義：google 網頁排名順序，請見
真實的特徵值物理意義：1940年美國華盛頓州的Tacoma Narrows懸索橋塌斷，有一說是強風引發自然頻率共振造成橋身斷裂。自然頻率是物體結構一旦在該頻率震動即可持續維持運動，像是我們小時候玩的盪鞦韆，人離開了，它還在持續擺動，後來人經過看見以為自己碰見鬼了。自然頻率的數學表達就是特徵值平方根。
請問老師：
特徵值eigen value與特徵向量eigen vector的意義，以二維、三維空間為例，用幾何圖示，可以理解為保持相同方向(角度)的向量伸縮。
聯想複變函數論的「保角映射」(conformal mapping)，可說是相同的概念嗎？或者，本質不同？
(我自己看書，學一點點「複變」，沒上正式課程，若問錯問題，敬請見諒！)
這個問題很難三言兩語說清楚，改日我再發文解釋。
感謝老師！
衷心企盼您寫出說明。
由老師您的另一篇文章 「從線性代數看微分方程」
————————————————
微分方程與線性代數都有特徵方程式 (characteristic equation) 一詞 . . . . . .
撇開微分方程底下偽裝的線性變換、零空間和通解的結構，僅就特徵方程式而言，微分方程與線性代數確實有著密切的關係。
————————————————
我猜想，不僅僅這兩門課有關聯，「eigen」的概念，好像也出現在許多其他地方。各種課程的教學，似乎很少有老師講出它們的共同點。
如果有人講出來，將有助大家把多領域的觀念，融會貫通，也能提升學習的樂趣！
今天(5/26/2014)刊登的每週問題就是conformal map，即一矩陣
的奇異值
(也就是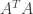 
的特徵值平方根)全都相同：
在微分幾何，
就是Jacobian矩陣。以2×2階矩陣為例，
isometric (保長映射)：
conformal (保角映射)：
equiareal (保積映射)：
因此，isometric=conformal+equiareal。
原來如此！
老師若沒講，我自己不會想到這些映射。
我想你應該有興趣知道MIT教授Gilbert Strang今年將出版一本新書：Differential Equations and Linear Algebra
http://math.mit.edu/dela/
我曾經買《線性代數的世界》，是翻譯自Gilbert Strang的著作。
今年這本新書，不知會不會有中文譯本？
或者，買英文書，搭配MIT開放課程影片來看。
我不知新書內容是否已有對應的影片？
Strang本人應該沒有錄製微分方程的video lectures。
MIT OCW, 18.03 SC, 講授者是Professor Arthur Mattuck
http://ocw.mit.edu/courses/mathematics/18-03-differential-equations-spring-2010/video-lectures/
http://ocw.mit.edu/resources/res-18-009-learn-differential-equations-up-close-with-gilbert-strang-and-cleve-moler-fall-2015/index.htm
剛好看到對應的影片，幫老師補充一下
请问一下，下面这个链接中p23页计算eigenvector是怎么一个过程？好像不太对？
Click to access ahptutorial.pdf
和我使用Octave计算出来的不一样，使用Octave的eig()函数算出来的值是一个复数。
引文的特徵向量算法稱為Power method，見下文
設初始向量為
，連續計算 
，並予以歸一化，至收斂停止。計算所得即為對應最大特徵值的特徵向量，見