矩陣的四個基本子空間基底算法

本文的閱讀等級：初級

令 $A$ 為一個 $m\times n$ 階實矩陣，也就是說 $A:\mathbb{R}^n\to\mathbb{R}^m$ 是一個線性變換 (見“線性變換與矩陣的用語比較”)。矩陣 $A$ 的值域 (range) 即為其行空間 (column space)

$C(A)=\{A\mathbf{x}\vert\mathbf{x}\in\mathbb{R}^n\}$ 。

將矩陣 $A$ 以行向量 (column vector) 表示為 $A=\begin{bmatrix} \mathbf{a}_1&\cdots&\mathbf{a}_n \end{bmatrix}$ ，其中 $\mathbf{a}_j\in\mathbb{R}^m$ 。因為

$A\mathbf{x}=\begin{bmatrix} \mathbf{a}_1&\cdots&\mathbf{a}_n \end{bmatrix}\begin{bmatrix} x_1\\ \vdots\\ x_n \end{bmatrix}=x_1\mathbf{a}_1+\cdots+x_n\mathbf{a}_n$ ，

$C(A)$ 就是行向量 $\mathbf{a}_1,\ldots,\mathbf{a}_n$ 的線性組合形成的集合。矩陣 $A$ 的核 (kernel) 即為其零空間 (nullspace)，記為

$N(A)=\{\mathbf{x}\in\mathbb{R}^n\vert A\mathbf{x}=\mathbf{0}\}$ 。

對於 $n\times m$ 階轉置矩陣 $A^T$ ， $C(A^T)$ 稱為 $A$ 的列空間 (row space)， $N(A^T)$ 稱為 $A$ 的左零空間 (left nullspace)。為什麼有這個奇怪的名稱？考慮 $A^T\mathbf{y}=\mathbf{0}$ ，等號兩邊取轉置可得 $\mathbf{y}^TA=\mathbf{0}$ ，因為 $\mathbf{y}^T$ 在 $A$ 的左側，故名左零空間。以上是實矩陣 $A$ 的四個基本子空間，其中列空間 $C(A^T)$ 和零空間 $N(A)$ 是 $\mathbb{R}^n$ 的子空間，行空間 $C(A)$ 和左零空間 $N(A^T)$ 是 $\mathbb{R}^m$ 的子空間 (見“線性代數基本定理 (二)”)。本文介紹一個矩陣的四個基本子空間的基底算法 (類似問題見“每週問題 April 6, 2009”)：以基本列運算 (elementary row operation) 化簡給定的矩陣 $A$ 至簡約列梯形式 (reduced row echelon form)，再從所執行過的列運算與最後的結果取出各子空間的基底向量。

我們先將 $m\times n$ 階矩陣 $A$ 和單位矩陣 $I_m$ 合併為一個增廣矩陣 $\begin{bmatrix} A&I_m \end{bmatrix}$ ，接著以基本列運算化簡直到產生簡約列梯形式。列運算過程可表示為一連串的矩陣乘法，引入 $I_m$ 的目的即在記錄所執行過的淨運算。令 $m\times m$ 階矩陣 $E=E_k\cdots E_1$ 代表對應列運算的基本矩陣乘積 (見“特殊矩陣 (10)：基本矩陣”)。基本列運算的化簡過程可表示如下：

$E\begin{bmatrix} A&I_m \end{bmatrix}=\begin{bmatrix} EA&EI_m \end{bmatrix}=\begin{bmatrix} R&E \end{bmatrix}$ ，

上面我們令 $m\times n$ 階矩陣 $R=EA$ 為 $A$ 的簡約列梯形式。設 $r=\mathrm{rank}A$ ，明顯地， $r\le\min\{m,n\}$ 。矩陣秩 $r$ 給出四個基本子空間維數 (即基底向量數，見“線性代數基本定理 (一)”)：

$\dim C(A^T)=r,~~\dim N(A)=n-r,~~\dim C(A)=r,~~\dim N(A^T)=m-r$ 。

因為簡約列梯形式 $R$ 的軸行 (pivot column，包含軸的行) 總數等於 $r$ ，故可表示成分塊矩陣

$R=\begin{bmatrix} I_r&F\\ 0&0 \end{bmatrix}$ ，

其中 $r\times r$ 階單位矩陣 $I_r$ 對應軸行， $r\times (n-r)$ 階分塊 $F$ 對應非軸行，零列包含 $(m-r)\times r$ 階和 $(m-r)\times (n-r)$ 階兩個零分塊。我們設定上述分塊矩陣形式僅為了方便推導，實際上，軸行未必都位居領先行 (請參考底下的例子)。令 $E=\begin{bmatrix} E_1\\ E_2 \end{bmatrix}$ ，其中 $E_1$ 是 $r\times m$ 階分塊， $E_2$ 是 $(m-r)\times m$ 階分塊。所以，最終結果具有下列形式：

$\begin{bmatrix} R&E \end{bmatrix}=\begin{bmatrix} I_r&F&E_1\\ 0&0&E_2 \end{bmatrix}$ 。

這個分塊結構連同關係式 $R=EA$ 提供了描述 $A$ 的四個基本子空間的充足資訊，下面解說如何推導它們的基底。

列空間 $C(A^T)$

基本列運算的作為是列的線性組合，因此不改變矩陣的列空間，可知 $C(A^T)=C(R^T)$ 。簡約列梯形式 $R$ 的 $r$ 個非零列 (即軸列) 是一個線性獨立集，表明分塊 $\begin{bmatrix} I_r&F \end{bmatrix}$ 的所有列向量構成 $A$ 的列空間的一組基底。

零空間 $N(A)$

基本列運算非但不改變矩陣的列空間，也不改變零空間，故 $N(A)=N(R)$ 。簡約列梯形式 $R$ 唯一決定 $n\times (n-r)$ 階零空間矩陣 (nullspace matrix)

$P=\begin{bmatrix} -F\\ I_{n-r} \end{bmatrix}$ ，

很容易確認 $RP=0$ (見“零空間的快捷算法”，“行空間與零空間的互換表達”)。因為 $P$ 的行向量是一個線性獨立集，它們構成 $A$ 的零空間的一組基底。

行空間 $C(A)$

基本列運算改變了矩陣的行空間， $C(A)\neq C(R)$ ，因此僅由簡約列梯形式 $R$ 無法推知 $A$ 的行空間。但基本列運算不改變行向量之間的線性組合關係 (見“左乘還是右乘，這就是問題所在”)，因為這個緣故， $R$ 的軸行指標就是 $A$ 的線性獨立行向量指標，故知 $A$ 的這些線性獨立行向量集構成 $A$ 的行空間的一組基底。

左零空間 $N(A^T)$

寫出

$EA=\begin{bmatrix} E_1A\\ E_2A \end{bmatrix}=\begin{bmatrix} I_r&F\\ 0&0 \end{bmatrix}=R$ ，

其中 $E_2A=0$ 說明 $E_2$ 的列向量屬於左零空間 $N(A^T)$ 。基本矩陣乘積 $E$ 是一個可逆矩陣，必有線性獨立的列向量，所以分塊 $E_2$ 的列向量集構成了 $A$ 的左零空間的一組基底。

底下舉一個例子說明矩陣的四個基本子空間基底的計算程序。考慮 $4\times 5$ 階矩陣

$A=\begin{bmatrix} 2&6&2&2&2\\ 1&3&1&1&1\\ 3&9&3&4&5\\ 1&3&1&2&3 \end{bmatrix}$ ，

求 $C(A^T)$ ， $N(A)$ ， $C(A)$ 和 $N(A^T)$ 的基底。

步驟 1：以基本列運算將 $\begin{bmatrix} A&I_4 \end{bmatrix}$ 化簡至簡約列梯形式 $\begin{bmatrix} R&E \end{bmatrix}$ 。結果如下：

$\begin{bmatrix} 2&6&2&2&2&\vline&1&0&0&0\\ 1&3&1&1&1&\vline&0&1&0&0\\ 3&9&3&4&5&\vline&0&0&1&0\\ 1&3&1&2&3&\vline&0&0&0&1 \end{bmatrix}\to \left[\!\!\begin{array}{ccccrcrrrr} 1&3&1&0&-1&\vline&-17&28&4&5\\ 0&0&0&1&2&\vline&27&-43&-6&7\\ 0&0&0&0&0&\vline&-13&20&3&-3\\ 0&0&0&0&0&\vline&4&-6&-1&1 \end{array}\!\!\right]$

步驟 2：將重要的結果整理出來。簡約列梯形式 $R$ 的 1, 4 行是軸行，故 $r=2$ ， $n-r=3$ 。提取主要分塊並寫出零空間矩陣：

$\begin{bmatrix} I_r&F \end{bmatrix}=\left[\!\!\begin{array}{ccccr} 1&3&1&0&-1\\ 0&0&0&1&2 \end{array}\!\!\right],~~E_2=\left[\!\!\begin{array}{rrrr} -13&20&3&-3\\ 4&-6&-1&1 \end{array}\!\!\right],~~P=\left[\!\!\begin{array}{rrr} -3&-1&1\\ 1&0&0\\ 0&1&0\\ 0&0&-2\\ 0&0&1 \end{array}\!\!\right]$ 。

步驟 3：寫出各子空間的基底。

列空間 $C(A^T)$ 的基底由 $\begin{bmatrix} I_r&F \end{bmatrix}$ 的列向量組成：

$\left[\!\!\begin{array}{r} 1\\ 3\\ 1\\ 0\\ -1 \end{array}\!\!\right],~~\left[\!\!\begin{array}{c} 0\\ 0\\ 0\\ 1\\ 2 \end{array}\!\!\right]$ 。

零空間 $N(A)$ 的基底由 $P$ 的行向量組成：

$\left[\!\!\begin{array}{r} -3\\ 1\\ 0\\ 0\\ 0 \end{array}\!\!\right],~~\left[\!\!\begin{array}{r} -1\\ 0\\ 1\\ 0\\ 0 \end{array}\!\!\right],~~\left[\!\!\begin{array}{r} 1\\ 0\\ 0\\ -2\\ 1 \end{array}\!\!\right]$ 。

行空間 $C(A)$ 的基底包含 $A$ 的軸行，即第 1, 4 行：

$\left[\!\!\begin{array}{c} 2\\ 1\\ 3\\ 1 \end{array}\!\!\right],~~\left[\!\!\begin{array}{c} 2\\ 1\\ 4\\ 2 \end{array}\!\!\right]$ 。

左零空間 $N(A^T)$ 的基底由 $E_2$ 的列向量組成：

$\left[\!\!\begin{array}{r} -13\\ 20\\ 3\\ -3 \end{array}\!\!\right],~~\left[\!\!\begin{array}{r} 4\\ -6\\ -1\\ 1 \end{array}\!\!\right]$ 。

8 Responses to 矩陣的四個基本子空間基底算法

Mu says:

04/25/2013 at 5:30 pm

老师您好，非常喜欢您写的现代启示录，概念讲得特别简练清楚。我尤其喜欢概念中几何意义的引申，很有启发，打算认真读完。谢谢！
另外，这篇文章的开始，定义部分是不是有些拼写错误？C(A), column space, 是不是“列空间”，而C(A^T),row space,则表示“行空间”？

- ccjou says:
  
  04/25/2013 at 6:40 pm
  
  歡迎來訪。你點出的問題很有趣。既不是你誤讀，也不是我寫錯，這是因為兩岸對於「行」與「列」用法不同而生的誤會。請見
  
  兩岸線性代數用詞參照
  
  哪麼是甚麼原因造成的呢？這個嘛，我也不知道。
  
Transform says:

02/13/2016 at 8:31 pm

老師您好想請問你一些觀念
如圖上式=號是成立的嗎
我下面假設了一個例子它們的向量一樣
但一個是列表示一個是行表示這樣也算等於嗎?

因為最近碰到類似的題目有解題老師說 col(A^T)與Row(A) 算同構但不等於
不知這觀念是不是錯的?
希望老師解惑

- ccjou says:
  
  02/13/2016 at 10:30 pm
  
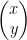  二維向量可以寫成 $(x,y)$ 或 $\begin{pmatrix} x\\ y \end{pmatrix}$ ，但如果視為矩陣，則 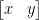$\begin{bmatrix} x&y \end{bmatrix}$ 與 $\begin{bmatrix} x\\ y \end{bmatrix}$ 的意義就不同。
  
  $\hbox{col}(A^T)$ 是 $A^T$ 的行向量擴張的子空間， $\hbox{row}(A)$ 是 $A$ 的列向量擴張的子空間，兩者是相同的子空間， $\hbox{col}(A^T)=\hbox{row}(A)$ 。我們說子空間 $V=U$ ，若 $V$ 與 $U$ 在同一個向量空間內，且 $V\subset U$ ， $U\subset V$ 。關於同構子空間的討論請見
  
  同構的向量空間
  
  - Transform says:
    
    02/13/2016 at 10:53 pm
    
    老師所以我上面空間展延的橫 [1 0] 和直的[1 0] 是向量而非矩陣所以兩個其實是一樣的只是在表示時可以用直的或橫的來表示一個向量可以這樣理解嗎
    
    - ccjou says:
      
      02/14/2016 at 8:27 am
      
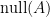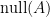      是的。再舉個例子， $\hbox{null}(A)$ 是 $A\mathbf{x}=\mathbf{0}$ 的解形成的子空間， $\hbox{null}(A)$ 裡的向量該怎麼規範直的或橫的？從書寫上來看應該是直的，也就表示 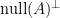$\hbox{null}(A)^\perp$ 不等於 $\hbox{row}(A)$ ，因為 $\hbox{row}(A)$ 包含橫的向量。幾何向量區分直橫只會製造麻煩。
      
      - Transform says:
        
        02/14/2016 at 9:55 am
        
        對我之前就有這樣直橫的問題
        感謝老師的解答我懂了
        
Alexander Lin says:

01/15/2023 at 9:43 pm

In the example, how did you get the basis vectors for the left nullspace? The vectors a=[ -1 2 0 0] and b=[1 0 -1 1] can form a basis for the left nullspace. And [-13 29 3 -3]=10a + (-3)b; [4 -6 -1 1]=(-3)a + b.

	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明
	悟 on 條件機率與貝氏定理
	jeremy on 內積與外積是怎麼來的？