本文的閱讀等級:中級
令 為一個向量函數。對於
維實向量
,
具有下列形式:
,
其中 ,
是
的定義域。例如,極座標至卡氏座標的轉換是一個向量函數:
,
其中 ,
。如果向量函數
的數學形式相當複雜,線性化是一個常用的簡化方法。針對單變量函數
,在
附近我們可用直線
近似
。推廣至多變量函數,令
為一個仿射 (affine) 變換 (見“仿射變換”),表示如下:
,
其中 是一個
階實矩陣,
。下面解釋如何以仿射變換
近似向量函數
,由此衍生
的導數矩陣,稱為 Jacobian 矩陣 (或簡稱 Jacobian),隨後介紹 Jacobian 行列式與其應用,以及 Jocabian 矩陣與 Hessian 矩陣的關係。
Jacobian 矩陣
我們的目標是在 的鄰近範圍使用形式較簡單的仿射變換
近似
。既然
是聚焦點,我們要求
。因為
,就有
,或
,所以
。
接著要找出 使得仿射變換
在
點附近最近似
。自然地,當
趨於
,符合最近似條件的
應使誤差
更快速地趨於
(零向量)。若存在一個
階實矩陣
使得
,
我們說 在
可導 (differentiable)。為了讓
可從任何方向逼近
,我們另要求
是定義域
的一個內點 (interior point),意思是鄰近
的所有點都屬於
。
下面證明若向量函數 在
點可導,則
由
唯一決定。考慮
的標準基底
,其中
的第
元為
,其餘元為
。設
為一極小數使得
,
,屬於定義域
。如果
在
可導,就有
。
因為 ,可知
。
上式等號左邊即為偏導數
,
等號右邊等於矩陣 的第
行,故
。
這個 階矩陣稱為向量函數
在
的 Jacobian 矩陣或導數矩陣 (derivative matrix),記為
。因此,可導函數
在
的最佳仿射近似是
。
設 ,則
的泰勒展開式為
。
因為 ,
。
上式指出仿射變換的改變量 是自變量的改變量
的線性函數,Jacobian 矩陣
即為線性變換矩陣。直白地說,當我們將非線性函數予以線性化時,Jacobian 矩陣就是描述該線性關係的矩陣。
看兩個計算的例子。若 ,則
。
若 ,則
。
不令人意外,,線性映射的 Jacobian 矩陣即為變換矩陣。
回到本文初給的例子,極座標至卡氏座標轉換的 Jacobian 矩陣計算如下:
。
若 是極座標平面上的一條曲線,
是卡氏座標平面上的映射曲線,使用鏈式法則 (chain rule),
和
具有下列關係:
。
從幾何上說,Jacobian 矩陣將極座標平面的切向量映至卡氏座標平面的切向量。
Jacobian 行列式
若 是可導函數,則 Jacobian 是一個
階矩陣,因此可計算行列式。下面我們討論 Jacobian 行列式的意義和用途。為方便說明,設
,向量函數
將
映至
,則
的 Jacobian 行列式為
。
令 表示
和
所張的長方形,其中
和
是微小量。若
和
足夠接近
,則
近似下列向量所張的平行四邊形 (見“線性變換把面積伸縮了”):
,
。
令 代表平行四邊形
的面積。因為二階行列式的行向量所張的平行四邊形面積等於行列式的絕對值 (見“行列式的運算公式與性質”),
。
所以,微小區域 經向量函數
映射至
,其面積伸縮了
倍。
Jacobian 行列式最主要的應用在多重積分的換元積分法 (integration by substitution)。令 為一個連續實函數,且
和
是一對一可導函數。根據上述面積變化關係式,可推得下面的變數變換積分公式:
。
以極座標至卡氏座標的變數變換為例,考慮 ,求
在
的積分。從極座標區域
映至卡氏座標區域
是一對一映射,因為
,
且 在
是一對一函數。Jacobian 行列式為
。
利用換元積分公式可得
。
Jacobian 與 Hessian
最後補充說明 Jacobian 和 Hessian 矩陣的關係。設 為二次可導函數,
,
階實對稱矩陣
稱為
的 Hessian (見“Hermitian 矩陣與實對稱矩陣的一些實例”),定義如下:
。
又 於
的梯度 (gradient)
定義為一個
維向量,其中第
元是
對
的一次偏導數,即
。
梯度 是一個向量函數,
的 Jacobian 矩陣如下:
,
因此證明梯度 的 Jacobian 即為
的 Hessian 矩陣。


老師,jacobian行列式為轉換因子從幾何證明最多證到三維,那要如何證明推廣到n維依舊是轉換因子@@?
證明關鍵在於行列式的幾何意義, 階行列式表示
階行列式表示 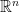 空間中平行多面體的有號體積,請見下文:
空間中平行多面體的有號體積,請見下文:
老師,我看了你上面的文章,所以是dxdydz…..這式子成立必須dx,dy,dz彼此間互相正交(因為才不會互相影響),在不同座標系微分後有(dx,dy,dz)^T=A(du,dv,dt,)^T,(A為一矩陣),將dx,dy,dz取出後視為向量再將各向量正交化後由上面文章知道dxdydz=|A|dudvdt而|A|即為Jacobian。
老師這樣想是對的嗎@@?
我們不能說「dx,dy,dz彼此間互相正交」,dx,dy,dz是微小的純量,應該說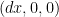 ,
, ,
, 三個向量彼此正交。請再仔細讀一遍上文
三個向量彼此正交。請再仔細讀一遍上文  表達式的推導過程,
表達式的推導過程, 代表微小長方形
代表微小長方形 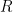 經線性變換
經線性變換 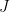 (Jacobian) 後的面積。
(Jacobian) 後的面積。
老師 我不懂什麼是平行多面體,如果只是在二維跟三維可以用平行四邊形跟平行六面體的體積來解釋,可是四維以上後平行多面體的體積是什麼東西@@?
這是幾何學的一個抽象概念,請參閱維基百科的超方形(Hypercube)的介紹:
http://zh.wikipedia.org/wiki/%E8%B6%85%E6%96%B9%E5%BD%A2
線性代數是平面與空間解析幾何至高維空間的一種推廣。
老師,這實在是有點難懂囧…
我能理解你的疑惑。
清大數學系「數學組」和「應數組」的必修課程最大的不同之處在於前者包含二學期「幾何」,後者則無。
http://www.math.nthu.edu.tw/riki1/riki.php?id=%E5%A4%A7%E5%AD%B8%E9%83%A8%E8%AA%B2%E7%A8%8B&CID=1
老师你好。在文章里,你说到若存在一个m*n的实阶A使得那个极限(其实就是P点的导数)等于0,我们说F在P可导。我很奇怪,可导的条件不是左极限等于有极限吗?为什么文章里写的是极限等于零呢?
請參考這個網站
http://mathinsight.org/differentiability_multivariable_definition
那个极限等于零是不是意味着A是P处的切平面所对应的线性变换?
A是P处的切平面所对应的线性变换,並不是精確地描述。上文有兩個計算的例子,你看看或許就明白了。
請參考這篇貼文
完全明白了,谢谢!
梯度 \nabla f:\mathbb{R}^n\to\mathbb{R} 是一個向量函數,是不是應該f:\mathbb{R}^n\to\mathbb{R}^n