本文的閱讀等級:初級
在最佳化與機器學習領域,譬如線性規劃、線性判別分析 (linear discriminant analysis)、Logit 模型 (logistic regression) 和多層類神經網路 (multilayer network),超平面 (hyperplane) 是一個常見的模型元件。許多最佳化方法,如梯度下降法、Lagrange 乘數法和對偶理論,也都與超平面有關。本文從幾何與代數兩種觀點介紹超平面的基礎知識,並以凸集為例說明超平面於分割向量空間的應用 (見“凸組合、凸包與凸集”)。
在三維空間中,一平面上的所有點 受方程式
規範。推廣至一般幾何座標空間
,超平面定義為下列線性方程的所有解
形成的集合:
,
其中 是不全為零的實數,
也是實數。給定
,超平面
的向量表達式即為
。
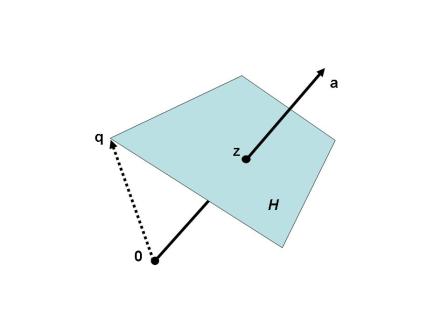
除了上面的代數定義,超平面還有等價的幾何定義。若 是
的一個子空間,
自原點平移
後所成的集合
稱為仿射空間 (affine space,見“仿射組合與仿射空間”),記作
。
因為仿射空間 由子空間
生成,我們指定
的維數等於
的維數。在
中,超平面是一個維數等於
的仿射空間。換句話說,除了
本身,超平面是具有最大維數的仿射空間 (見下圖)。
超平面的代數定義等價於幾何定義,論證於下。
代數定義幾何定義:設
,
。令
是
中任一向量。將
平移
可得一向量集
。對於任一
,
,即有
。但
,可知
,表明
是
階非零矩陣
的零空間。因為
,根據秩—零度定理
,可知
,即證明
是一個
維仿射空間。
幾何定義代數定義:設
是一個維數等於
的仿射空間。考慮
,將
平移
得到
;由仿射空間的定義可知
是一
維子空間。令非零向量
屬於正交補餘
,其維數等於
。據此,
。令
。對於任一
,
同義於
,也就有
,意味
。因為
,上半部證明已確定
的維數等於
,故證明兩向量集相等。
接著說明超平面的一些幾何性質。我們知道 的一平面將空間分割為兩個半空間 (half space)。同樣地,超平面
將
分成閉 (closed) 正半空間與閉負半空間,表示如下:
。
若等號不成立,則有開 (open) 正半空間與開負半空間:
。
明顯地, 和
的聯集即為
,且
、
以及
的聯集也為
。超平面
的方向 (orientation) 由法向量
決定,
至原點的距離則與純量
有關。令
為距離原點最近的點。根據正交原則,
必位於穿越原點,指向方向為
的直線上,因此
。(另一個說法,
是
中任一點至法向量
的正交投影。) 將上式代入超平面表達式,
,可得
。所以
,
至原點的距離即為
。
超平面常應用於分離 的向量集。定理一說,給定凸集外的任一點,必存在一穿越該點且不與凸集相交的超平面[1]。
定理一:若 為一有界 (bounded) 閉凸集,且
是
之外的一點,則存在一向量
使得
[2]。
因為 是
之外的點,故可令
。設
位於
的邊界使得
。下面我們證明
滿足命題條件。對於
且
,由凸集定義可知點
屬於
,即有
。
展開可得
。
當 ,上式通除以
,可得
。
乘開化簡,
設 即證得所求。
從幾何面來看,定理一宣稱給定凸集 之外的一點
,我們可以找到一穿越
的超平面
,稱為分離 (separating) 超平面,使得凸集
被超平面的一個開半空間
或
所包含 (見下圖左)。設想點
朝凸集
移動,超平面也隨之漸進移動。在連續的改變過程中,當
位於
的邊界時,必存在一支持 (supporting) 超平面,意思是
不僅穿越
的一個邊界點,而且
被
的一個閉半空間
或
所包含 (見下圖右)。我們將這個結果放在下面的定理。
定理二:若 為一有界閉凸集且
是
的一邊界點,則必存在一支持超平面穿越點
。
超平面所定義的半空間是凸集,多個閉半空間的交集也是一凸集,稱為多胞形 (polytope)。此類特殊凸集出現在各式各樣的應用中,譬如,線性規劃和賽局理論 (game theory)。這個主題將留待他日另文介紹。
來源與註解:
[1] 定理與證明取自 David G. Luenberger 所著 Linear and Nonlinear Programming,第二版,1984, 頁466-470。
[2] 表示最大下界 (infimum) 而非極小值 (minimum)。兩者的差異在於最大下界必定存在,極小值則未必存在。譬如,
是正有理數集合,
不存在最小值,但
。


妄自猜測一下,老師最近的一系列文章都應該是為simplex method做準備吧?
是的。先前我在
底下有云:
在討論可行解集合(滿足所有約束等式與不等式的解)的性質與單形法之前,我們最好先瞭解一些線性代數很少討論的向量空間幾何知識,如凸組合、超平面和多胞形(polytope)。所以等我寫完這些介紹文之後才會有線性規劃(二)。
這樣太好了。我看了不少關于線性規劃的課程,無論是美國的還是大陸的,都很少從這個角度講述線性規劃,大部分都只關于如何建模或者解題。從線性代數角度講述這個主題的,就我所見過的課程就只有convex programming了,但這個課程應該是屬于EE的研究生課程吧。
別的學校我不清楚,交大電控所開授的Optimization Theory不討論Linear Programming,內容集中在向量空間方法。
老師~~請問一下您有email嗎~~
我有關於待四函數如何證明是為正負定or不定矩陣的問題想要請教老師~~
但這裡沒有辦法複製上去,所以我想要電子郵件的方式寄給老師,再給我一點方向~~
我的email:flymancarter@gmail.com
概似函數
已將email address貼上留言版。
老師~~信件已經寄出~~麻煩老師抽空看一下~~
我將問題轉成pdf
Click to access question.pdf
符號解釋:
Click to access e7aca6e8999fe8a7a3e9878b.pdf
經濟學的模型怎麼都這麼複雜呀?傷腦筋。明天課後我再仔細看看。對了,你說的問題是甚麼?
謝謝老師nn
問題是要怎麼證明對所有控制變數的二階微分矩陣為正定負定或者是不定矩陣~~??
跟老師說一下~~
整個概似函數取ln去證明也可以也應該會比較好做~~~
雖然我看不懂你寫的式子(虛擬變數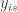 ,
, 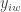 沒有出現在函數裡),還是將做法寫出:
沒有出現在函數裡),還是將做法寫出: 取對數改成
取對數改成  ,其中
,其中 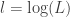 ,這時
,這時 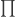 變成
變成 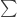 。
。 ,
, ,設為零,解出
,設為零,解出 和
和 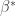 。
。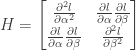 。
。 ,
,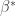 ,即有
,即有 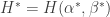 。因為是極大化問題,我們想確定二階方陣
。因為是極大化問題,我們想確定二階方陣 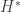 是半負定矩陣,也就是說,
是半負定矩陣,也就是說, 是半正定矩陣。你可以檢查主子陣的行列式,請見
是半正定矩陣。你可以檢查主子陣的行列式,請見
(1)
(2) 計算
(3) 計算 Hessian matrix
(4) 代入
老師我大概看了一下依然有以下一些小問題~~
1.因為我想要知道的是否為全域極大,且式子中的阿法跟貝塔和嘎瑪都為向量所以是否有一個矩陣表示的hessian矩陣可以說明~~??
2.若矩陣A為對稱矩陣則其特性向量所形成之矩陣亦為對稱!!??
1) 若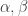 是向量,Hessian matrix
是向量,Hessian matrix 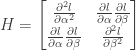 的主對角元
的主對角元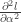 要改為Hessian 分塊
要改為Hessian 分塊 ![[\frac{\partial^2 l}{\partial\alpha_i\partial\alpha_j}]](https://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%5Cpartial%5E2+l%7D%7B%5Cpartial%5Calpha_i%5Cpartial%5Calpha_j%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,非主對角元
,非主對角元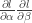 要改為分塊
要改為分塊 ![[\frac{\partial^2 l}{\partial\alpha_i\partial\beta_j}]](https://s0.wp.com/latex.php?latex=%5B%5Cfrac%7B%5Cpartial%5E2+l%7D%7B%5Cpartial%5Calpha_i%5Cpartial%5Cbeta_j%7D%5D&bg=ffffff&fg=333333&s=0&c=20201002) 。其他亦同。
。其他亦同。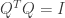 ,但
,但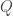 未必對稱。見
未必對稱。見
2) 實對稱矩陣的特徵向量構成的矩陣是一正交矩陣,即
謝謝老師~~
問題已解決~~感恩nn
老師,最近我在看統計學習的書籍中的分類問題,有一個疑問:應該如何判斷某一數據集合是否線性可分?不知到這個問題是否已經有解答,但我有的書中沒找到相關信息,望老師指點。
判定一組數據集是否線性可分(LS)並不是一件非常容易的事。下文列舉了一些測試方法,但未必總是有效:
Click to access IEEETNN06.pdf
以文中提到的neural networks(應該稱Perceptron)來說,若數據集是LS,則保證學習過程於有限次數停止並可得到一分割超平面。但若數據集是NLS,則學習過程不可能停止,這時我們又如何確定究竟是學習尚未結束(LS情況),還是根本就永不停止(NLS情況)?
近期我會另文介紹一些以超平面為判別函數(discriminant functions)的線性分類法。