最佳化理論與正定矩陣

本文的閱讀等級：中級

最佳化理論 (優化理論，optimization theory) 提供許多應用於社會、自然與工程科學的數值算法。給定一個目標函數或稱成本函數 $f:\mathbb{R}^n\to\mathbb{R}$ ，無約束優化 (unconstrained optimization) 是指找到 $\mathbf{x}\in\mathbb{R}^n$ 使得 $f(\mathbf{x})$ 有最小值，表示如下：

$\displaystyle \min_{\mathbf{x}\in\mathbb{R}^n}f(\mathbf{x})$ 。

在一些應用場合，如果我們希望找到最大值，只要改變目標函數的正負號即可。對一般的目標函數 $f$ ，這是一個很困難的問題，通常我們願意接受局部最小值 (稍後詳述)，意思是在某個範圍內的最小值。底下我們先考慮單變數的目標函數，隨後再推廣至多變數函數。本文的主旨在介紹無約束優化的一些基本概念並解釋正定矩陣於判定極值 (最大或最小) 存在性的用途。

令 $f:D\to\mathbb{R}$ 為一個定義於 $D\subseteq\mathbb{R}$ 的光滑可導實函數，其中 $D$ 是一個開集。泰勒 (Taylor) 定理說 $f(x)$ 可表示為下列展開式：

$f(x)=f(y)+\displaystyle{f'(y)}(x-y)+\frac{f''(y)}{2}(x-y)^2+O(|x-y|^3)$ 。

若 $f'(y) =0$ ，我們稱 $y$ 為 $f$ 的一個駐點 (stationary point)，也稱臨界點 (critical point)。若 $|x-y|$ 足夠小，鄰近 $y$ 的 $f$ 函數近似於一個二次函數：

$\displaystyle f(x)-f(y)\approx \frac{f''(y)}{2}(x-y)^2$ 。

如果 $f''(y)>0$ ，我們稱 $y$ 為一個局部最小值 (local minimum)。嚴謹的說法是：存在一個 $\delta>0$ ，對於所有 $x$ 滿足 $\vert x-y\vert\le\delta$ 都有 $f(y)\le f(x)$ 。如果 $f''(y)<0$ ，我們稱 $y$ 為一個局部最大值 (local maximum)。又如果 $f''(y)=0$ ，則必須直接計算 $f(x)$ 和 $f(y)$ 才能決定 $y$ 的屬性。因此， $f'(x^\ast)=0$ ，即駐點 $x^\ast$ 是函數 $f$ 的一個局部最小值的必要條件。

前述單變數分析可延伸至多變數問題，假設函數 $f$ 由 $n$ 個變數 $x_1,x_2,\ldots,x_n$ 所控制，令向量 $\mathbf{x}=(x_1,\ldots,x_n)^T$ ， $f(\mathbf{x})$ 為定義於 $D\subseteq\mathbb{R}^n$ 的可導實函數，泰勒定理的多變數形式為

$\displaystyle \begin{aligned} f(\mathbf{x})&=f(\mathbf{y})+\sum_{i=1}^n\left.\frac{\partial f}{\partial x_i}\right|_{\mathbf{y}}(x_i-y_i)\\ &~~~+\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\left.\frac{\partial^2f}{\partial x_i\partial x_j}\right|_{\mathbf{y}}(x_i-y_i)(x_j-y_j)+O(\Vert\mathbf{x}-\mathbf{y}\Vert^3).\end{aligned}$

定義函數 $f$ 於點 $\mathbf{y}$ 的梯度 (gradient) 為一個 $n$ 維向量，其中第 $i$ 元為 $f$ 對於 $x_i$ 的一次偏導數，如下：

$\nabla f(\mathbf{y})\overset{\underset{\mathrm{def}}{}}{=}\displaystyle\begin{bmatrix} \left.\frac{\partial f}{\partial x_1}\right|_{\mathbf{y}}\\ \vdots\\ \left.\frac{\partial f}{\partial x_n}\right|_{\mathbf{y}} \end{bmatrix}$ 。

另定義 $n\times n$ 階矩陣 $H(\mathbf{y})$ 為 $f$ 於點 $\mathbf{y}$ 的 Hessian 矩陣，其 $(i,j)$ 元為 $f$ 的二次偏導數，如下：

$[H(\mathbf{y})]_{ij}\overset{\underset{\mathrm{def}}{}}{=}\displaystyle\left.\frac{\partial^2f}{\partial x_i\partial x_j}\right|_{\mathbf{y}}$ 。

多變量泰勒定理可用矩陣形式表示為

$\displaystyle f(\mathbf{x})=f(\mathbf{y})+\nabla f(\mathbf{y})^T(\mathbf{x}-\mathbf{y})+\frac{1}{2}(\mathbf{x}-\mathbf{y})^TH(\mathbf{y})(\mathbf{x}-\mathbf{y})+O(\Vert\mathbf{x}-\mathbf{y}\Vert^3)$ 。

若 $\mathbf{y}$ 是一個駐點，即 $\nabla f(\mathbf{y})=\mathbf{0}$ ，當 $\Vert\mathbf{x}-\mathbf{y}\Vert$ 足夠小，

$\displaystyle f(\mathbf{x})-f(\mathbf{y})\approx\frac{1}{2}(\mathbf{x}-\mathbf{y})^TH(\mathbf{y})(\mathbf{x}-\mathbf{y})$ 。

使用導數法則，

$\displaystyle\frac{\partial^2f}{\partial x_i\partial x_j}=\frac{\partial^2f}{\partial x_j\partial x_i}$ ，

可知 $H(\mathbf{y})$ 是一個對稱矩陣。若 $H(\mathbf{y})$ 是正定的，即 $\mathbf{z}^TH(\mathbf{y})\mathbf{z}>0$ ，可知 $\mathbf{z}\neq\mathbf{0}$ ， $\mathbf{y}$ 是 $f$ 的一個局部最小值 (見“特殊矩陣 (6)：正定矩陣”)；反之，若 $H(\mathbf{y})$ 是負定的，則 $\mathbf{y}$ 是 $f$ 的一個局部最大值。見圖一，目標函數

$f(x_1,x_2)=e^{-x_1^2-x_2^2}+1.5e^{-(x_1-2)^2-(x_2-2)^2}$

有兩個局部最大值在 $(0,0)$ 和 $(2,2)$ 。

圖一具有兩個局部最大值的函數

如果 $H(\mathbf{y})$ 是未定的，則 $\mathbf{y}$ 稱為鞍點 (saddle point)，例如， $f(x_1,x_2)=x_1^2-x_2^2$ ，其梯度為 $\nabla f=(2x_1,-2x_2)^T$ ，Hessian 是

$H=\left[\!\!\begin{array}{cr} 2&0\\ 0&-2 \end{array}\!\!\right]$ 。

因為 $H$ 有特徵值 $2$ 和 $-2$ ，可知 $H$ 是未定的，函數 $f$ 的鞍點在 $(0,0)$ ，見圖二。

圖二具有一個鞍點的函數

給定一個可導實函數 $f(\mathbf{x})$ ，如何找出其局部最小值呢？如要找尋 $f(\mathbf{x})$ 的局部最大值可轉換為找尋 $-f(\mathbf{x})$ 的局部最小值。這個問題屬於最佳化理論的範疇，下面我介紹一個常用的一階演算法，稱為梯度下降法 (gradient descent)。梯度下降法假設已知一個初始點 $\mathbf{a}$ ，你站在該點沿著 $f$ 的最陡下降方向移動，該方向即為 $f$ 於點 $\mathbf{a}$ 的梯度相反方向，算式如下：

$\mathbf{b}=\mathbf{a}-\eta\nabla f(\mathbf{a})$ ，

其中 $\eta>0$ 表示移動的步伐大小。只要 $\eta$ 足夠小且 $\nabla f(\mathbf{a})\neq\mathbf{0}$ ，便可以保證 $f(\mathbf{b})<f(\mathbf{a})$ ，利用泰勒定理可證明此性質。考慮 $f(\mathbf{b})$ 於點 $\mathbf{a}$ 的泰勒展開式：

$\displaystyle f(\mathbf{b})-f(\mathbf{a})=\nabla f(\mathbf{a})^T(\mathbf{b}-\mathbf{a})+\frac{1}{2}(\mathbf{b}-\mathbf{a})^TH(\mathbf{a})(\mathbf{b}-\mathbf{a})+O(\Vert\mathbf{b}-\mathbf{a}\Vert^3)$ 。

將梯度下降法給出的關係式 $\mathbf{b}-\mathbf{a}=-\eta\nabla f(\mathbf{a})$ 代入上式，得到

$\displaystyle f(\mathbf{b})-f(\mathbf{a})=-\eta\Vert\nabla f(\mathbf{a})\Vert^2+\frac{\eta^2}{2}\nabla f(\mathbf{a})^TH(\mathbf{a})\nabla f(\mathbf{a})+O(|\eta|^3)$ 。

不論 $H(\mathbf{a})$ 是正定、負定或未定的，我們總能選擇夠小的正數 $\eta$ 使得 $f(\mathbf{b})-f(\mathbf{a})<0$ 。

我將梯度下降法整理於下：給定一個初始點 $\mathbf{x}_0$ ，根據遞迴公式

$\mathbf{x}_{n+1}=\mathbf{x}_n-\eta_n\nabla f(\mathbf{x}_n)$ ，

就有

$f(\mathbf{x}_0)\ge f(\mathbf{x}_1)\ge f(\mathbf{x}_2)\ge\cdots$ 。

適當選擇夠小的步伐 $\eta_n$ ，向量序列 $\{\mathbf{x}_n\}$ 最終會收斂至 $f$ 的一個局部最小值。看下面的例子^[1]：　

$f(x,y)=\displaystyle\sin\left(\frac{1}{2}x^2-\frac{1}{4}y^2+3\right)\cos\left(2x+1-e^y\right)$ 。

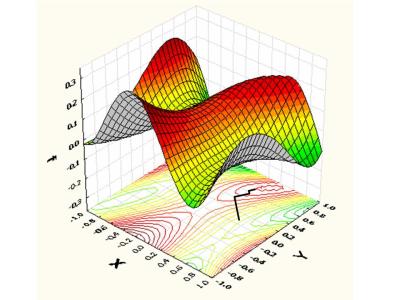
如果我們希望找尋局部最大值，可將梯度下降改為梯度上升 (gradient ascent)，也就是選擇 $\eta<0$ 。圖三顯示三維空間函數面圖形與平面輪廓圖的梯度上升軌跡，明顯地，梯度上升法收斂至哪一個局部最大值由給出的初始點位置所決定。

圖三梯度上升過程

註解
[1] 取自維基百科http://en.wikipedia.org/wiki/Gradient_descent

5 Responses to 最佳化理論與正定矩陣

張盛東 says:

04/29/2013 at 12:46 am

老師，請問一下上面那個泰勒定理的多變量形式的二次項是否少了係數 1/2 呢？

- ccjou says:
  
  04/29/2013 at 7:52 am
  
  謝謝指正。錯誤還不少，一併訂正了。
  
  - 張盛東 says:
    
    08/25/2013 at 10:18 am
    
    老師，文章的開頭，若y是f(x)的局部最小值，那麼對所有滿足|x-y|=f(y),不等號的方向反了吧？
    
    - ccjou says:
      
      08/25/2013 at 11:36 am
      
      感謝指正。難怪出版社需要editor，書寫者總是看不到自己的錯誤。
      
張盛東 says:

08/25/2013 at 12:50 pm

說來慚愧，我也是第二次讀老師的文章的時候才發現。

	jianglong on Strassen 演算法──分治矩陣乘法
	jianglong on Strassen 演算法──分治矩陣乘法
	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明