每週問題 June 26, 2017

Posted on 06/26/2017 by ccjou

對於秩-1方陣 A，證明 \det (A+I)=\hbox{trace}A+1。

Let A be an n\times n matrix and \hbox{rank}A=1. Prove that \det (A+I)=\hbox{trace}A+1.

 
參考解答：

證明1. 使用 Schur 三角化定理。存在一個么正矩陣 (unitary matrix) U，U^\ast=U^{-1}，使得 A=UTU^\ast，其中 T 是上三角矩陣且 \hbox{rank}T=1，即

T=\begin{bmatrix} t_{11}&t_{12}&\cdots&t_{1n}\\ 0&0&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&0 \end{bmatrix}。

使用跡數循環不變性，

\begin{aligned} \det(A+I)&=\det(UTU^\ast+UIU^\ast)=\det(U(T+I)U^\ast)\\ &=(\det U)\det(T+I)(\det U^\ast)=\det(T+I)=t_{11}+1\\ &=\hbox{trace}T+1=\hbox{trace}(U^\ast AU)+1=\hbox{trace}(AUU^\ast)+1\\ &=\hbox{trace}A+1. \end{aligned}

 
證明2. 令 A=\mathbf{u}\mathbf{v}^T，其中 \mathbf{u} 與 \mathbf{v} 為非零向量。使用 Sylvester 行列式定理，

\begin{aligned} \det(A+I)&=\det(\mathbf{u}\mathbf{v}^T+I)=\det (\mathbf{v}^T\mathbf{u}+1)=\mathbf{v}^T\mathbf{u}+1\\ &=\hbox{trace}(\mathbf{v}^T\mathbf{u})+1=\hbox{trace} (\mathbf{u}\mathbf{v}^T)+1\\ &=\hbox{trace}A+1. \end{aligned}

This entry was posted in pow 行列式, 每週問題 and tagged , . Bookmark the permalink.

4 Responses to 每週問題 June 26, 2017

  1. m010114 says:
    01/15/2018 at 2:35 pm

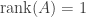    因為\mathrm{rank}(A)=1，所以A必有一個非零的eigenvalue，設此值為\lambda，且0必為A的eigenvalue，0的multiclipity為n-1。依此，A可以對角化。

    令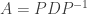A=PDP^{-1}為A的eigen decomposition，則

    \mathrm{det}(A+I)=\mathrm{det}(P(D+I)P^{-1})=\mathrm{det}(D+I)=\lambda + 1 = \mathrm{trace}(A)+1

    Reply
  2. 胡霖 says:
    03/23/2018 at 12:15 pm

    秩1矩阵不一定能对角化吧！例如，A=[0 1; 0 0]，A的两个特征值都是0，rank=1，但是不能对角化。

    Reply
  3. Alanear says:
    10/20/2020 at 10:45 pm

    A+I的特征方程：（-1）^n X^(n-1)(X-traceA),令X=-1代入

    Reply
    • Alanear says:
      10/21/2020 at 3:52 pm

      笔误，前面是A，此外，应该可以从特征向量的角度直接从几何上说明，A有一个非0特征向量a，A*a=traceA*a,I*a=1*a,左右相加，因为特征值就是对应特征向量的拉伸系数，A+I作用在a上的效果就是它行列式的作用效果，所以等式成立。

      Reply

Leave a comment