本文的閱讀等級:初級
對首次接觸特徵分析的學者來說, 像是從天上掉下來的禮物。表面上,人人面露喜悅之情欣然接受;私底下,個個心中不免納悶:「這個神奇的式子究竟是怎麼冒出來的?」教書多年,我當然清楚學生的疑惑,參考了各家說法之後,決定採用一個省時省力的問題導入方式。每回開始講解特徵分析前,我會先介紹一階常微分方程
,並說明解為
,其中
是純量。緊接著延伸至高階微分方程,寫出對應的矩陣表達式:
。
從一階微分方程的解,我們猜想解向量的形式為 ,將它代回微分方程式,可得
。
等號兩邊消去 就得到
。我的原意是告訴大家:「你看多奇妙啊,微分方程轉換成特徵方程了。」不過這套論述難脫倒果為因之譏,一不小心可能會誤導學生以為特徵分析的原始動機只是為了解微分方程。
真正具有說服力的學習動機衍生自探索過程。最初我們根據某種假設或指導原則行事,偶然發現了一些特殊現象,好奇心激起我們深入探討它發生的原因,從而發展出一套理論。數學的發現也有一些基本指導原則,探索線性代數問題的一個有效方法是「透過各種變換的不變性質來掌握核心概念與技巧」。下面我就從這個角度切入線性變換的特徵值問題。
線性變換將向量空間裡的一個子空間映射 (或移動) 至另一個子空間,子空間的不變性就是通往另一間密室的鑰匙。設 為定義於向量空間
的一個線性變換。對於子空間
,令
表示子空間
中所有向量經過
映射得到的像 (image) 所成的集合,即
。
向量空間 經
映射所成的集合
稱為
的值域 (range),記為
。若
是一個線性變換參考某個基底的表示矩陣,值域
即為
的行空間
。不難驗證,
也是
的子空間。如果
,我們稱
是線性變換
的一個不變子空間 (invariant subspace)。零向量
滿足
,
是一個平凡的不變子空間,我們對它不感興趣。
下面我用一個簡單的例子說明不變子空間的效用。考慮 階方陣
,
且向量集 為
的一組基底:
。
令 ,
。分別計算
,
,如下:
對於任意 ,
因為
所以 是一個不變子空間,但
並非不變子空間。上面三個式子可用矩陣表示為
。
令基底矩陣 ,也就有
。
上式中 是線性變換
參考基底
的表示矩陣。
觀察發現 具有較簡化的分塊上三角形式,這個現象提示我們,找到越多的不變子空間就可以得到更為簡化的矩陣。將上例的子空間
替換為
,
,計算得到
,
因此確認 也是一個不變子空間。線性變換
參考新基底
的表示矩陣具有分塊主對角形式:
。
將上例推廣至一般情況。考慮 階方陣
,設
為不交集的不變子空間,即
,
。令
,滿足
。收集各子空間
的基底向量可組成
的一組基底
。若
的行向量依序由這些基底向量構成,則
是可逆矩陣,且
,
其中 是
階分塊。如果每個不變子空間的維數都等於
,即
,就有
,
其中 是純量。對角矩陣是我們所能得到最為簡約的形式,這時
稱為可對角化矩陣。
高斯消去法將矩陣化簡為簡約列梯形式,我們也預期存在某種方法可將矩陣分塊對角化,甚至如果可能的話,將它完全對角化。上例顯示關鍵在於尋找所有維數等於 的不變子空間,自然也就有下面的問題陳述:設
為
擴張的子空間,且
。若
,則必有純量
使得
,其中
稱為
的特徵值,
稱為對應
的特徵向量。從不變子空間切入特徵值問題不僅有合理明確的動機,也有聯繫向量空間和座標變換的作用。問題在於近年出版的基礎線性代數課本已將向量空間分析壓縮至最小範圍,因此隻字不提不變子空間。學生缺少這個工具,教師只好退而求其次,找出替補辦法,最後勉強選擇一個典型應用作為特徵分析的研究動機。

請問老師:
最初為何數學家選用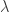 這個符號代表「特徵值」?
這個符號代表「特徵值」?
看老師的DVD,好像稍微有提到符號來源,我希望知道更詳細一些。
回想自己的求學歷程,第一次看到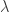 ,應該是國三物理學,「波長」的代表符號,當年班上沒人問老師,老師也沒說,大家就寫這個符號。有升學壓力的情況下,能夠得分就好,大概沒人有時間去思考符號的來源。
,應該是國三物理學,「波長」的代表符號,當年班上沒人問老師,老師也沒說,大家就寫這個符號。有升學壓力的情況下,能夠得分就好,大概沒人有時間去思考符號的來源。
經過二十多年,有一天,我突然想到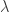 相當於L,而「波長」(Wave Length),
相當於L,而「波長」(Wave Length),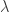 可以聯想L代表Length。
可以聯想L代表Length。
能夠聯想的符號,可以幫助記憶。這是一項遲來的發現,假如國中老師有說明,當年寫這個符號,應該心裡會比較舒適。
我查維基百科,想瞭解Eigen,知道它來自德文,可翻譯為「自身的」,「特定於…的」,「有特徵的」或者「個體的」。但這與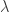 符號,如何聯想?仍未找到答案。
符號,如何聯想?仍未找到答案。
L或者lambda,都是代表Length。线性变换前后,特征向量的方向是不变的,但长度有可能变化。特征值表示特征向量长度的变化,所以用lambda表示。见于strange的书第六章。
字首”eigen”是德文,意思是”proper”或”characteristic”,所以中文譯為”特徵”,也有些人說”固有”。早年美國使用proper value,今天全球都統稱eigenvalue。特徵的概念很早就出現在許多數學領域,例如微分方程,在線性代數中最早使用eigenvalue一詞的人可能是德國數學家David Hilbert。至於為何選用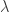 (lambda)來表示,這我就不清楚了。希臘字母常用於代表數學和科學領域的常數或變數,但字母本身其實並沒有什麼含意。
(lambda)來表示,這我就不清楚了。希臘字母常用於代表數學和科學領域的常數或變數,但字母本身其實並沒有什麼含意。
本來我想從一個功利的角度說明為何要研究特徵值和特徵向量:因為可以發大財賺大錢!
不信的話,請看 Google 背後的線性代數
The $25,000,000,000 eigenvector
Click to access googleFinalVersionFixed.pdf
有些時候, 希臘字母的選擇,可以聯想其意義,用起來的感覺比較好。
 符號
符號
 可以聯想 distance 或 difference
可以聯想 distance 或 difference
 可以聯想 error
可以聯想 error
例如微積分,在極限的章節,用了
假如完全不能聯想意義,好像到了陌生的新環境,東西用起來有怪怪的感覺。
無意義的符號,少量還可以,若是很多個符號皆很陌生,可能增加頭腦的負擔,讓學習出現障礙。當符號變成有意義時,大概學習會變得比較順利。
以上是個人推測,也許一般人感覺沒關係,符號不帶有意義,照樣可以學習,考試也能拿高分。
國中物理「波長」(Wave Length),用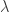 符號,我尚未知道
符號,我尚未知道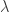 可以聯想 L (Length),只會照書本抄寫符號。
可以聯想 L (Length),只會照書本抄寫符號。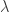 ,我開始自己發揮想像力,
,我開始自己發揮想像力,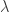 有點像中文字「人」,兩雙腳:一前一後,相當於走一步的距離。
有點像中文字「人」,兩雙腳:一前一後,相當於走一步的距離。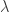 符號感覺熟悉,熟悉之後,學習變得比較順利。
符號感覺熟悉,熟悉之後,學習變得比較順利。
唸高中,物理學「波長」仍使用
而人走路的「速度」等於 (每分鐘走的步數) 乘以 (平均一步的長度)
這很像光速或音速的算法: (頻率) 乘以 (波長)
這樣的思考,讓我對
想到Length,竟然是在二十餘年之後。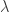 代表Length?
代表Length?
我不知道,英語為母語的國家,學生會不會自己很容易聯想
如果每個不變子空間的維度都是 1,即r_j=1,就有[A]_B =B^{-1}AB diag(d1,…,dn), 其中 d_j 為一純量。主對角矩陣是我們所能得到最為簡約的形式,這時 A 稱為可對角化矩陣。
老師,請問B^{-1}AB後面是不是少個等號?
還有…這件事怎麼証明呢?
(Friedberg書也有類似習題 p327,4th, ex36)
哈,感謝告知,B^{-1}AB 後面是少了個等號,已訂正。
上文只有說明,但沒有證明,我再抽空看看 Friedberg 的習題。也許當作每週問題貼上吧。
Friedberg 的習題如下: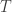 be a linear operator on a finite-dimensional vector space
be a linear operator on a finite-dimensional vector space 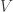 . Prove that
. Prove that 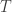 is diagonalizable if and only if
is diagonalizable if and only if 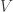 is the direct sum of one-dimensional
is the direct sum of one-dimensional 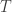 -invariant subspaces.
-invariant subspaces.
Let
設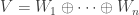 ,且
,且  ,對於任意
,對於任意 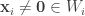 有
有  ,因為
,因為 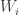 的維度等於 1,可知
的維度等於 1,可知 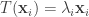 。因為
。因為 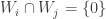 ,
,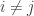 ,故
,故 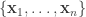 可為
可為 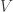 的一組基底,
的一組基底,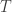 參考此基底的矩陣表達式為
參考此基底的矩陣表達式為
![[T]=\mathrm{diag}(\lambda_1,\ldots,\lambda_n)](https://s0.wp.com/latex.php?latex=%5BT%5D%3D%5Cmathrm%7Bdiag%7D%28%5Clambda_1%2C%5Cldots%2C%5Clambda_n%29&bg=ffffff&fg=333333&s=0&c=20201002)
即對角化矩陣。
為何 Friedberg 的課本不使用最直接的詞彙?例如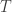 有
有 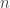 個線性獨立特徵向量,或每個特徵值的幾何重數等於代數重數,則
個線性獨立特徵向量,或每個特徵值的幾何重數等於代數重數,則 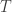 是可對角化的。不講
是可對角化的。不講  ,卻說它是有限維向量空間;不說特徵向量,而硬要說 1維不變子空間;不說存在
,卻說它是有限維向量空間;不說特徵向量,而硬要說 1維不變子空間;不說存在 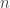 個線性獨立特徵向量,卻要說
個線性獨立特徵向量,卻要說 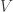 是1維不變子空間的直和;不用矩陣,而非要使用線性變換,縱使可對角化最後還是用矩陣來表示。
是1維不變子空間的直和;不用矩陣,而非要使用線性變換,縱使可對角化最後還是用矩陣來表示。
有沒有人知道到底是為什麼?
我覺得因為是習題,要是寫的那麼直白,就大家都會了。
我的見解如下:
此題的目的是想讓讀者思考當向量空間可寫成有限多個不同的一維的不變子空間時,要有一些解題上的觀念:上述的不變子空間為不同eigenvalues 所對應的 eigenspaces(原因是因為維度是1) , 還有另一個原因是題意較強調 ” 向量空間的直和 ” 這種空間觀念(較抽象) , 作者可能是希望讀者可以不要用到代數觀念(就像是代數重數相關的觀念) , 不用矩陣的原因是因為我們知道線性代數大致上可分為兩種觀點來看待每一題目的題意,分別是 1. 線性函數 2. 矩陣 (因為線性函數和矩陣是一體兩面) , 然而題目是用線性函數和向量空間的直和問此題 , 所以題目只是希望解題者多用一些空間上的觀念和定義解題 , 若有別的想法可和我討論 , 因為此種問題只有出題者最清楚 , 我只是經由讀完Friedberg的書後的想法來詮釋或是說明上述的問題
是因為主要是要談空間分解嗎?
空間分解=>光譜定理
空間分解=>投影
譜定理可以直接利用投影矩陣和基礎子空間分析解釋
我的問題是:明明是很簡單的「可對角化」,為什麼非要繞一大圈耗費這多力氣來導引呢?這樣不是很不符合成本效益嗎?
我覺得講linear operator是因為不需要談到”矩陣”吧,比較general(雖然最後還是用了矩陣是變得有點沒意義)
而說finite-dimensional vector space可能是強調出並非無限維空間,也就是無限維空間這個結論不會對..嗎@@?
一維不變子空間直和這就有點囉嗦了,如果寫這段話之前已有談過特徵向量,那好像就有點不必要,大概是他不想多一個符號 “n” 吧,或是附近才剛談到不變子空間,可以複習一下^^|||
或者是他覺得”一維不變子空間直和”和”可對角化”這兩件事可以直接感覺出關係吧,雖然我感覺不出來XD
TO GSX:
你詮釋的很中肯也很有趣。如果將 Friedberg 等人寫的 linear algebra 和另一本入門書 elementary linear algebra 拿來比較,幾乎感覺不出這兩本書是出自同樣的三位作者。我總好奇當作者寫作時,預想的讀者背景如何?寫作的目的究竟是傳遞訊息,自我表述(把自己知道的全記錄下來)抑或還有其他隱藏的意圖?回到可對角化問題,或許繞一大圈也不是壞事,總可以讓我們從多個角度來看同一件事情。
我這週末將外出,回來再想想你在討論區提的問題。
推測因為線性變換T:V->V
T的主要處理主角是vector space,
所以與T對應的要說不變子空間,而不說特徵向量
既然各位對於不變子空間的迴響有如此高的興致,改日我試著寫一篇從線性變換角度看不變子空間,循環子空間 (cyclic subspaces),向量空間分割(直和),與不變子空間基底(特徵向量和廣義特徵向量)的關係文好了。
或者大家還有更棒的建議亦可提出。
因為這樣寫看起來比較強比較專業,至於看書的人看得懂看不懂那顯然不是作者們考慮的
周老師您好: 請問假如有一個可對角化的矩陣A, 有n個distinct的eigenvectors且eigenvalues都不等於0
那它的eigenvectors是不是就可以生成CS(A)?
我的想法:
所有eigenvectors都包含於CS(A)且eigenvectors所生成的空間與CS(A)dimension相同, 所以是
請問是這樣嗎?