本文的閱讀等級:中級
奇異值分解 (singular value decomposition,以下簡稱 SVD) 被譽為矩陣分解的「瑞士刀」和「勞斯萊斯」[1],前者說明它的用途非常廣泛,後者意味它是值得珍藏的精品。在“線性代數基本定理 (四)”一文,我們介紹了 SVD 的推導,並於矩陣的四個子空間分析平台解釋其幾何涵義,本文簡述 SVD 重點並舉一例說明分解式的計算步驟。

美國史丹佛大學教授格魯布 (Gene Golub) 於矩陣運算的貢獻造就 SVD 成為今日最重要的線性代數應用 From http://www.cs.nyu.edu/overton/genearoundtheworld/gene.jpg
設 為一個
階實矩陣,
,SVD 具有以下形式:
,
其中 是
階,
是
階,
是
階。特別的是,方陣
和
都是實正交矩陣 (orthogonal matrix),也就是說,
,
,
是 (類) 對角矩陣,如下:
。
主對角元 ,
,且
,
,稱為奇異值 (singular values)。注意,SVD 的分解不具有唯一性。為了便利應用,我們習慣將奇異值由大至小排序:
。
利用圖示可以幫助我們了解 SVD 的矩陣結構。SVD 最特別的地方是 的多數元為零,圖一的白色區塊以及黃色區塊的非對角元皆為零。
令 的行向量 (column vector)為
,
,
的行向量為
,
,
可以表示為
個秩-1 (rank-one) 矩陣之和:
上式指出 僅由
的前
個行向量 (以
表示),
的前
個列向量 (以
表示),以及
的左上
分塊決定 (以
表示),稱為「瘦」奇異值分解,如圖二所示。這個結果看似不起眼,其實它有重大的意義。矩陣
總共有
個元,
有
個元,
有
個元,
則只需儲存主對角的
個非零元。若以 SVD 形式儲存,總計有
個元。當
遠小於
和
時,利用矩陣的 SVD 可以大幅減少儲存量。
我們可以將 SVD 視為變換矩陣 的三個分解步驟:旋轉
,伸縮
,再旋轉
,圖三顯示
階矩陣的分解變換。另一方面,
也可以視為變換矩陣
參考了基底
和
的主對角變換矩陣 (見“線性變換觀點下的奇異值分解”)。
SVD 的計算主要是利用下面幾個性質:
(1) 和
的非零特徵值為
,
,
。注意,
和
是半正定 (positive semidefinite) 矩陣,其特徵值必定不為負數。
(2) 的單位特徵向量為
,
。
(3) 的單位特徵向量為
,
。
(4) 對於 ,
和
具有以下關係:
對應奇異值 ,
稱為左奇異向量,
稱為右奇異向量。
底下舉一個例說明奇異值分解計算程序。考慮 階矩陣[2]
。
步驟 1:計算交互乘積矩陣 ,如下:
。
步驟 2:求 的特徵值與對應的特徵向量,將特徵值大至小排序:
,
對應的單位特徵向量依序為
。
非零奇異值為 ,
,
。
步驟 3:設定 和
:
,
。
步驟 4:最後計算 。對於
,此例
,可直接計算
,結果如下:
,
而 則由 Gram-Schmidt 正交化程序求出 (“Gram-Schmidt 正交化與 QR 分解”):
。
合併上面結果,
。
在“通過推導偽逆矩陣認識線性代數的深層結構”一文,我曾經介紹 SVD 於最小平方近似解的應用並一路推導出偽逆矩陣 (pseudo-inverse),從而徹底解決了線性方程的求解問題。了解該篇專欄內容需要相當的耐心與毅力,但付出絕對值得,因為這個主題是線性代數的聖母峰。
註解
[1] Gene H. Golub, Michacel W. Mahoney, Petros Drineas, and Lek-Heng Lim, Bridging the Gap Between Numerical Linear Algebra, Theoretical Computer Science, and Data Applications, SIAM News, Vol. 39, No. 8, 2006.
[2] 取自 維基百科:Singular value decomposition




u4算錯了,是[0;0;-1;0]
u4正交化是對哪個矩陣正交化?
Gram-Schmidt 正交化程序是說隨便挑一個向量不在
請問為何步驟2中, A^TA的特徵值是16,9,5,0,0, 而不是16,9,4,1,0
(1 -x)(16 -x)(9 -x)( -x)(4 -x) =
= (1 -x)*(16 -x)*(9 -x)*( -x)*(4 -x)
= -576*x +820*x^2 -273*x^3 +30*x^4 -x^5
= -x*(x -1)*(x -4)*(x -9)*(x -16)
這是5*5矩陣,你是不是把它當成3*3的公式解了…
(1 -x)(16 -x)(9 -x)( -x)(4 -x) =
= (1 -x)*(16 -x)*(9 -x)*( -x)*(4 -x)
= -576*x +820*x^2 -273*x^3 +30*x^4 -x^5
= -x*(x -1)*(x -4)*(x -9)*(x -16)
TO Edman,
你的算式十分複雜,我相信應該還有更好的計算方法。
今天讀了SVD一系列文章,真是太棒了! 有醍醐灌頂的感覺!XD 而且深感線性代數這門基礎學問,像是拼拼圖一樣,有趣極了!
有同學問如何快速計算上面 的特徵值?
的特徵值? 相似於
相似於
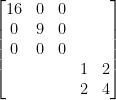
 的特徵值為16, 9, 0 和
的特徵值為16, 9, 0 和  的特徵值。因為
的特徵值。因為 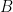 不可逆,故有一特徵值0,另一個特徵值即為
不可逆,故有一特徵值0,另一個特徵值即為 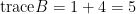 。
。
重新置換行列,
可知
老師 抱歉請您糾正我錯誤的觀念
將 矩陣A 之列行向量對調 其特徵值 應該會改變才對
兩相似矩陣的特徵值相等 這可以看懂
但如何快速地知道 transpose(A)*A 與上方那矩陣相似
還請老師指導
將上文 的列行排列
的列行排列 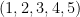 改成
改成  即可,詳見
即可,詳見
若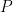 是一排列矩陣,
是一排列矩陣, ,故
,故  相似於
相似於  ,也就是說
,也就是說  與
與  有相同的特徵值。
有相同的特徵值。
感謝老師
這是我從沒想到的方法
真想親自聽您的課
另外 光碟並沒有針對內積空間做深入討論
真希望老師能出線代第二版的光碟
老師抱歉,請允許我談個「題外話」:
「禪」字,可分解為「示」與「單」,聯想到「簡單表示法」。
「單」可再分解為「口」、「口」、「田」、「十」。
「口」、「口」、「田」這三個字,看起來有點像矩陣的外廓。
「十」讓我想到分隔線,左上區為對角矩陣,右上、左下、右下區域皆為0。
老師說,SVD這個主題是線性代數的聖母峰。
如果說,SVD具有甚深禪意,是否可行?
(假如老師覺得這篇回應不妥,可以刪去,我不會在意。)
你的解文說字令人嘆為觀止,中文字裡面也有超乎部首的分解意涵。太有趣了!
確實我在教學光碟的最後一(或二)堂課也說過:SVD是線性代數的聖母峰。原因有二:(1)SVD幾乎涵蓋所有線性代數的核心概念(big idea),(2)「奇異值分解(SVD)」,即上面的這篇文章,總是霸佔本站“近期最多人點閱”的榜首(當然這是後話)。如果「禪」是“最高境界”的一種暗喻,那麼毫不猶豫地,我同意SVD深具禪意。
PS:系統管理員和我從未刪去讀者的任何迴響。少數迴響可能莫名其妙地不見了,那是因為以前的系統曾遭到病毒攻擊,不得已重灌系統造成部分資料流失。
AA^t 和 A^tA 做SVD有差嗎???@@
當看到題目給的矩陣不知道要怎麼判斷怎麼分解!
A^tA或AA^t都可求出SVD。你可以挑選其中階數較小或數值較簡單的,如果選擇AA^t,這時要使用上述性質(3),先解出奇異值和左奇異向量u,再計算右奇異向量v。你可以試試。
老師請問一下SVD方法可以判斷相依嗎??
可以。上文提及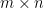 矩陣
矩陣  的矩陣秩
的矩陣秩 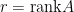 即為
即為  的非零奇異值總數,
的非零奇異值總數, 且
且 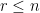 。若
。若 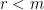 ,則
,則  有線性相依的列向量。若
有線性相依的列向量。若  ,則
,則  有線性相依的行向量。
有線性相依的行向量。
謝謝老師,那當矩陣相依,可以找出相依的係數嗎??
感激老師,現在非常需要判斷相依並且找出相依的係數
SVD 未能提供行向量或列向量的相依關係(組合係數)。不過,方才恰好有一位讀者談到這個問題,請見
做法:將給定矩陣
當一個非方陣矩陣 A 經 PseudoInverse 方法並乘上自己本身 A 的矩陣,如果不為單位矩陣代表矩陣式中有相依,想請問能有效直接判斷矩陣中哪一列為相依嗎??
感激老師不辭辛勞的解答
有關 的介紹請見
的介紹請見
挑選 的線性獨立行向量的最簡單做法是讓
的線性獨立行向量的最簡單做法是讓  的行向量經過一可逆線性變換,
的行向量經過一可逆線性變換, ,然後從結果判讀。
,然後從結果判讀。 必須具備簡單形式,譬如列梯形式或簡約列梯形式。
必須具備簡單形式,譬如列梯形式或簡約列梯形式。
SVD 方法能判斷 非線性獨立或相依嗎??
如果不行,想請問原因是因為??
謝謝老師…
令 是一
是一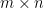 階矩陣。奇異值分解
階矩陣。奇異值分解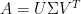 給出的
給出的 即為
即為 的行空間基底。從這個向量集無法推得
的行空間基底。從這個向量集無法推得 的線性獨立行向量集,但我們知道
的線性獨立行向量集,但我們知道 。若
。若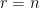 ,則
,則 有線性獨立的行向量。請參閱
有線性獨立的行向量。請參閱
有个问题想请教下,就是如何由性质(1)(2)(3)推导出性质(4)呢, ,
,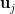 和
和 具有以下关系:
具有以下关系:
就是这个(4)对于
我將你的迴響編輯過以正確顯示LaTeX。方法是在指令前加入$latex,空一格,之後再以$結束。
合理的推導順序其實是(1)(2)(4)->(3)或(1)(3)(4)->(2),請參閱
或
又或者
如果今天不解,等明天再說吧。《亂世佳人》最後一句台詞,Scarlett 說:
“I’ll think of it tomorrow, at Tara. I can stand it then. Tomorrow, I’ll think of some way to get him back. After all, tomorrow is another day.”
嗯,你的这篇博客 “如果蘇利文是海倫凱勒的線性代數老師” 讲的比较详细,我会仔细看看,多谢热情的博主!
哈哈,第一次聽到有人說我熱情。等中午吃過飯有了力氣,下午我再寫一篇超級簡短的SVD推導好了。
這個就是
Reblogged this on leehwi and commented:
现代启示录
以前念書時一直感到疑惑,課本在教奇異值分解只舉實矩陣為例,若要推廣到複矩陣,莫非只要把運算過程中的轉置矩陣皆推廣成Hermitian即可?另外,算過幾次複矩陣,似乎奇異值分解過程中的對角化矩陣恆為實矩陣,這是因為(A^H)A(個人Hermitian符號習慣用H)為正定矩陣緣故?
寫到這裡,其實我最大的疑惑還是,不知為何線代授課時不在一開始便開宗明義定義複矩陣,由此建構整套系統?在面對複矩陣時,個人有時會有一知半解,知識建構不完整之感,需要上網查閱相關資料確認,不是不好,畢竟人的求知並不限於學校,但這也是否一方面意味著所學其實不甚完整,某些部分流於破碎?瀏覽過一些教科書,但目前發現課程章節的安排上大同小異,大都將複矩陣壓縮成一小節或甚至未獨立成篇,連帶影響了課程規劃,但我想這是編寫教材者本身授課理念以及如何詮釋一門學問核心價值的問題,這方面還有賴教授根據多年教學經驗,不吝分享想法,這樣的課程安排是否為普遍受現今學界認同,或者只是因為教材沒得選擇?
寫得有點囉嗦,謝謝教授不必勞苦的回覆訪客的問題
這個問題屬於教學法。使用實矩陣介紹SVD的優點有:(1) 多數學生較熟悉實矩陣,(2) 多數的應用僅涉及實矩陣;缺點有:失去完整性。當老師授課時,通常他設定的講授對象是全班在中位數的那些學生,後段與前段的學生可能都不會滿意這樣的內容鋪陳。另一方面,這年頭真的想要理解整套知識系統的學生也不是那麼普遍,沒有需求就沒有供給,教育也是一種市場。
嗯,不過依個人經驗,對於自然界的訊號處理,複矩陣在應用上會比較實際,我不清楚把矩陣分成實部和虛部處理會不會也是種方法?另外,可否再向教授確認個人問題前半部,關於推廣至複矩陣的情形,觀念上是否無誤?
好奇一問,教授是否有推薦的線代書籍,能兼顧實矩陣和複矩陣,疏通兩者觀念,建構整套知識系統?(其實這說法有點問題,所有矩陣歸根究柢應為同套系統,只是我想很多書可能 會從實矩陣出發,仍將複矩陣拆散成篇)或者,可否請教授分享經驗,在求學時代如何補足這方面課堂所學的不足?
再次感謝教授的回覆
1) 有些分析場合將實部與虛部區分開來,如旋轉矩陣的特徵值:
2) 複矩陣A的奇異值(對角)矩陣也由非負數組成,因為
3) 我知道的線性代數教材有:
其中數學專業用書都應開符合你的需要。
老師您好 感覺瘦svd分解與資料探勘中的技術有關?! 若對資料(table m*n)做SVD分解 至於中間的矩陣所儲存下來的奇異值是主成份囉? 有沒有什麼理解方法,不知道怎麼串在一起
SVD與資料矩陣的關係可以從兩個面向理解。
矩陣近似:
主成分分析:
令 U 的行向量為 \mathbf{u}_j,V 的行向量為 \mathbf{v}_j,A=U\Sigma V^T 可以表示為 r 個秩-1(rank-one)矩陣之和
应该是U的列向量吧
關於用詞說明請見下文:
想請教老師一個問題,SVD 的性質(4)是通過證明得到的?還是直接定義的?這裡讓我產生了困惑,因為我嘗試對 SVD 性質(4)進行推導,但是發現無法導出,最終在 [這份資料](http://www.math.tau.ac.il/~turkel/notes/SVD.pdf) 中我找到了對於性質(4)的說明解釋是『we define』….
此外,感謝老師,看了您的博客受益良多,另外關於機器學習當中,有很多矩陣求導的問題,網上的講解十分混亂,有些甚至自相矛盾,不知道您是否有時間開這樣一個專題呢,拜謝~
從推導過程來看,u是被定義出的一個向量,見下文
關於矩陣求導請參考
感謝老師的回復,我的問題都已解決。
想請教一個相關證明題,如何證明A*B的最大奇異值<=A的最大奇異值*B的最大奇異值,不知從何下手,麻煩老師解惑了。
老师,文中的latex未正确显示为文本
謝謝告知,我察覺沒有所有未正確顯示的公式指令 中含有”換行(line breaks)”,Wordpress 使用的latex rendering可能更新過才發生這個問題。我查了wordpress forum以前也有人碰過這個問題,wordpress 沒有回覆:
中含有”換行(line breaks)”,Wordpress 使用的latex rendering可能更新過才發生這個問題。我查了wordpress forum以前也有人碰過這個問題,wordpress 沒有回覆:
https://en.forums.wordpress.com/topic/beginaligned-in-mathmode-seems-to-have-stopped-working/
目前我也不知道有甚麼解決方案。
我修改latex code後本篇可正常顯示, 但至少要一星期才能改完所有文章,特此致歉。