序
線性代數者,代數之支也。此學究方程解而來,以結構為本,空間為體,變換為法,演算為用耳[一]。凡學者斷不可不知,而亦至不易究也;蓋其體系洸洋瑰麗,理論精微博大,匯泰西疇人(註一)之大略,集百家藝學(註二)之菁華。初,制定義,設公理;及後,論證明,演算法。徐光啟曰:「不用為用,眾用所基。」線代一門,取經用宏,肆應不窮,可謂當今應數之大功,算學之大成耳。是故銳心學者當奮不顧身,戮力鑽研,索理究解,切毋思逸而廢焉。
今之數學源于西洋,言事體例殊異華夏。維基大典記曰[二]:「蓋當今之世,數學之事,誠難僅以文述,而無符號,故凡數學之文,咸有漢字、拉丁字相易之事。舉本文為例,甲(A)之示,即文句以甲代一物,算式以A代之,以合文言、數學,則無論文理之人,咸可明之也。」文言簡練,古典雍容,故宜講談數學,格物窮理。然私竊不遜,未通其道,遂網搜谷歌,探徵維基,頓獲貼文數篇,特採錄之。顧選文散落舛雜,迄無定本,是以不揣荒陋,研核擘析,刪其遊辭,取其典實,裨補疎遺,引致旁徵,務使義理通達而群可閱之也。經涉一宿,幸可成卷,凡三篇,名曰「線代入道要門論」。
一 矢量空間
矢量空間者,歐幾里得空間之引伸也,亦曰線性空間、向量空間,究之者,線性代數也[二]。
定義
矢量空間者,交換群()也,其物曰矢量或向量,合一域(
),曰標量域,其物曰標量或純量。交換群者,乘法合交換律之群也,故矢量可以加法謂之。矢量加法者,矢量加矢量得矢量(
)。矢量合標量有標量乘法。標量乘法者,標量乘矢量得矢量(
)。矢量加法與標量乘法必以下是從(網連“同構的向量空間”):
■ 矢量甲乙之和,同乎乙甲之和(),曰交換律。
■ 矢量甲乙之和加矢量丙,同乎甲加乙丙和(),曰加法結合律。
■ 矢量單位元曰零(),零加甲得甲(
)。
■ 矢量逆改曰負,甲必有一負甲,其和為零()。
■ 標量甲乙之積乘矢量丙,同乎甲乘乙丙之積(),曰乘法結合律。
■ 標量一乘矢量甲得甲()。
■ 標量甲乘矢量乙丙之和,同乎甲乙積加甲丙積(),曰分配律。
■ 標量甲乙之和乘矢量丙,同乎甲丙積加乙丙積(),亦曰分配律。
若標量為實數,曰實矢量空間。若標量為複數,曰複矢量空間。矢量空間之最小生成集,曰基。基之大小,曰維數。
例
域直積(),域之物為標量,維數為域之數(
)。
多項式集,實數為標量,維數無窮。
二 範空間
範空間者,範之所也。夫範,物之長也[三]。
定義
範空間者,實矢量空間或複矢量空間也,凡矢量(),略稱物,必有一數,曰範(
)。凡範者,必以下是從(網連“矩陣範數”):
■ 範者,非負也()。範為零者,零也(
)。
■ 標量乘物之範,同乎標量之絕對值乘物之範()。
■ 二物和之範,不大於物範之和矣()。此謂三角不等式也。
二物其差之範,度量也()。故範空間實度量空間也。
例
歐幾里得空間者,高維實空間()合一範也。凡一點,合其各部之方,取開方,則得歐幾里得範(
)。
三 內積空間
內積空間者,矢量空間合一內積也。夫內積者,關乎範、角也。凡物之範與二物所交之角,可由內積定之[四]。
定義
凡二物必有一數,曰內積()。凡內積者,必以下是從(網連“內積的定義”):
■ 矢量甲乙之內積,同乎乙甲內積之軛()。
■ 矢量甲與乙丙和之內積,同乎甲乙與甲丙內積之和()。
■ 矢量甲與標量丙乘矢量乙之內積,同乎丙乘甲乙之內積()。
■ 物與己之內積,非負也()。零者,零也(
)。
物與己內積開方,範也()。故內積空間必範空間也。
例
歐幾里得空間,取二物,合各部之積,曰點積()。二物點積除其範之積,求餘弦之逆,曰二物之夾角也(
)。
實多項式之集,取二物,其積之有限積分(),亦內積也。
跋
太史公曰:「蓋西伯拘而演周易;仲尼厄而作春秋;屈原放逐,乃賦離騷;左丘失明,厥有國語;孫子臏腳,兵法修列;不韋遷蜀,世傳呂覽;韓非囚秦,說難孤憤;詩三百篇,大抵聖賢發憤之所為作也。此人皆意有所鬱結,不得通其道,故述往事,思來者。」余作入道要門,論次其文(註三),既非意有所鬱結,亦不思垂空文以自見(註四),實乃興會之所屬也。蓋余居新竹山陰,蒼梧之野,是日朝雨夕煙,四望茫然。時飯飽酒足,烹茶品茗,興之所至,几案網遊,撫筆電,擊鍵盤,為文自娛,公諸同好,良為快事矣。
誌于庚寅年三月十一(公曆二〇一〇年四月二十四日)。
註
一:精於天文曆算之學者,或謂數學家。
二:數學者,古六藝之一也。
三:採集編修,固無創新耳。
四:垂之青簡,照耀千秋。
引據
維基大典有云:「凡我維基之文,悉為共享創意授權。翻印增刪,皆須引據,並同道為之。」若所刪節補訂者,刊本具存,豈妨繙讀。
[一]:http://zh-classical.wikipedia.org/wiki/%E4%BB%A3%E6%95%B8
[二]:http://zh-classical.wikipedia.org/wiki/%E7%9F%A2%E9%87%8F%E7%A9%BA%E9%96%93
[三]:http://zh-classical.wikipedia.org/wiki/%E7%AF%84%E7%A9%BA%E9%96%93
[四]:http://zh-classical.wikipedia.org/wiki/%E5%85%A7%E7%A9%8D%E7%A9%BA%E9%96%93

拜讀大俠妙文,爽快!爽快!
結構為「本」,空間為「體」,變換為「法」,演算為「用」。
請問大俠,何者為「相」?
心經曰:「諸法空相。」試舉一例,矩陣何也?一曰:「矩陣者,矢量也。矩陣集必矢量空間也。」一曰:「矩陣者,函數也。矩陣乃線性變換也。」
《六祖壇經》師(六祖惠能)一日思惟:「時當弘法,不可終避。」遂出至廣州法性寺;值印宗法師講涅槃經。因二僧論風幡義,一曰風動,一曰幡動,議論不已。師進曰:「不是風動,不是幡動,仁者心動。」
蓋迷之即垢,悟之即淨,縱之即凡,修之即聖。善線代之法,不著相、勤用功而已矣。
好,我同意,不著相。
金剛經:「凡所有相,皆是虛妄!」
不著相是大道理,說的容易,行之困難。學者難免為相所惑,譬如, 究竟為何?
究竟為何? 為係數矩陣,
為係數矩陣,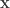 為未知數向量;
為未知數向量; 的行向量之線性組合,則
的行向量之線性組合,則 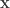 各元為組合權重;
各元為組合權重;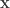 經變換矩陣
經變換矩陣  映射得到的像,則
映射得到的像,則 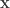 為輸入向量。
為輸入向量。
(1) 可以視為聯立方程等號左側的表述,則
(2) 可以讀作
(3) 可以看成
經曰:「見見之時,見非是見,見猶離見,見不能及。」(見見的大家頭昏腦脹!)線性代數難學之處,原因可能在於相不斷隨著情境而變,既非一定,故言之虛妄。
沒討論區發問,提在底下:
$$$$ 是$$R^n$$中標準內積,且 $$||a||^2 = $$, $$S:= \{a\in R^n | ||a|| = 1\}$$. 令 $$A$$是nxn 實方陣,且考慮 $$f(x) = $$, $$x \in S$$。假設 $$a\in S$$, 存在一正數 $$\delta > 0 $$, 使得 $$f(a) \geq f(x)$$, 對所有 $$x\in S$$ 滿足 $$||x-a|| < \delta$$。那麼我們可以說: $$f(a)\geq f(x)$$ 對所有 $$x\in S$$ 成立嗎? prove or disprove it.
找到一個反例: $$A=\begin{bmatrix}
1 & 0 & 0\\
0 & 0 & 0\\
0& 0 & 0
\end{bmatrix}$$, $$x=[1, 0, 0]$$, $$a=[1/\sqrt{3}, \sqrt{2}/\sqrt{3}, 0]$$.
這樣可以嗎? 有誤解題目意思嗎?
疑…竟然張貼失敗…..有些符號還消失~@@”
$ $ 是$ R^n $中標準內積,且 $ ||a||^2 = $, $ S:= \{a\in R^n | ||a|| = 1\} $. 令 $ A $是nxn 實方陣,且考慮 $ f(x) = $, $ x \in S $。假設 $ a\in S $, 存在一正數 $ \delta > 0 $, 使得 $ f(a) \geq f(x) $, 對所有 $ x\in S $ 滿足 $ ||x-a|| < \delta $。那麼我們可以說: $ f(a) \geq f(x) $ 對所有 $ x\in S $ 成立嗎? prove or disprove it.
找到一個反例: \[ A=\begin{bmatrix}
1 & 0 & 0\\
0 & 0 & 0\\
0& 0 & 0
\end{bmatrix} \], $$ x=[1, 0, 0] $$, $$ a=[1/\sqrt{3}, \sqrt{2}/\sqrt{3}, 0] $$.
這樣可以嗎? 有誤解題目意思嗎?
wordpress.com 的 LaTeX 語法和傳統不同,請參閱
我將問題改好如下:
找到一個反例:
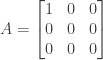 ,
, ![x=[1, 0, 0]](https://s0.wp.com/latex.php?latex=x%3D%5B1%2C+0%2C+0%5D&bg=ffffff&fg=333333&s=0&c=20201002) ,
, ![a=[1/\sqrt{3}, \sqrt{2}/\sqrt{3}, 0]](https://s0.wp.com/latex.php?latex=a%3D%5B1%2F%5Csqrt%7B3%7D%2C+%5Csqrt%7B2%7D%2F%5Csqrt%7B3%7D%2C+0%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
這樣可以嗎? 有誤解題目意思嗎?
問題中 f(x)=? 後面還有東西嗎?
有,只要是內積符號內的都不見了! 『a, b內積』是標準內積,…,||a||^2 = a, a內積,…,考慮 f(x)= x, Ax內積,….
再試下去會有洗版之嫌 orz……希望老師看得懂我的題目 >_<~
消失的部分: 是標準內積,……………., ||a||^2 = ,……., 考慮f(x)= ,….
好怪! 內積符號$$ $$ 出不來耶~ 上面指: “a, b內積”是標準內積,…,”||a||^2 = a, a內積”,…,考慮”f(x)= x, Ax內積”,……
老師真不好意思,不知怎麼修改迴響,佔了一堆版面…
標準內積語法是 a^{\prime}b, ,而
,而  。
。
是這樣嗎?
我上面是打內積符號: “左括、右括 “出不來 ……不過一樣啦^^
重寫一次問題如下,請 levinc417確定後再回覆。
找到一個反例:
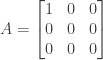 ,
, ![x=[1, 0, 0]^T](https://s0.wp.com/latex.php?latex=x%3D%5B1%2C+0%2C+0%5D%5ET&bg=ffffff&fg=333333&s=0&c=20201002) ,
, ![a=[1/\sqrt{3}, \sqrt{2}/\sqrt{3}, 0]^T](https://s0.wp.com/latex.php?latex=a%3D%5B1%2F%5Csqrt%7B3%7D%2C+%5Csqrt%7B2%7D%2F%5Csqrt%7B3%7D%2C+0%5D%5ET&bg=ffffff&fg=333333&s=0&c=20201002) .
.
這樣可以嗎? 有誤解題目意思嗎?
ok. 麻煩老師了
不客氣。
先去吃點東西,到辦公室再說了。