本文的閱讀等級:中級
假設 階實矩陣
有線性獨立的行向量 (column vector)。如何求得 QR 分解
,其中
階矩陣
的行向量組成單範正交集 (orthonormal set),
為
階上三角矩陣?
將 和
以行向量表示,並以上三角矩陣
聯繫,
即為
。
乘開上式,
。
我們的問題要解出 和
。但這不是一般所見的線性方程組,該怎麼辦呢?
線代箴言:「解題之道無他,求其放心而已矣。」意思是說,把失去的「本心」找回來就行了。單範正交集 滿足
,這裡
是 Kronecker 記號:
若
,
若
。上式左乘
,
,使用正交性
,可得
。
再將前一式改寫為
,
其中 ,否則
,與假設
相矛盾。將上式括弧內的向量表示為
,使用歸一性
,可得
。至此所有的運算公式皆已找齊,剩下的工作不過是將它們整理成一個算法膠囊:
Gram-Schmidt 正交化
- 對於
,
- 對於
,
-
-
-
-
解讀如下:第一, 是
在
方向的正交投影成分;第二,
是
扣除在
方向的正交投影之後的殘餘量;第三,
是向量
的長度;第四,
是
方向的單位向量 (unit vector)。
最後我們用下面的膠囊表總結 Gram-Schmidt 正交化與 QR 分解的運算程序 (以 為例):
閱讀方式係由左而右,從上往下。第一個輸入向量 直接給出
,計算其長度
,兩者「相除」立得
。針對第二個輸入向量
,先計算
,接著從
扣除投影分量
得到
,最後再計算
和
。按此方式類推可得到完整的
和
。
相關閱讀:

Column vector 应该是列向量吧。
請下文說明:
老師請問
若A 矩陣 行向量 沒有獨立的話 QR分解是否不存在 或沒意義?
A = [1 0]T [0 1] 這樣也算QR分解嗎?
[1 0]T 為線性獨立的矩陣 [0 1]也為上三角矩陣 但不為方陣
還麻煩請老師指導
你何不自己驗證一下結果?
http://www.bluebit.gr/matrix-calculator/
以下是我試驗的結果
A = QR
QR分解 A不一定要行獨立
Q與R不一定要為方陣 但Q之列向量為標準正交
transpose(Q) Q = I
結論為 任意矩陣均存在QR分解
transpose(Q) Q = I
R為上三角 不一定為方陣
不盡然如你所述。試輸入下列矩陣:
 。
。 的行向量線性相關時,
的行向量線性相關時,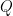 的行向量確實是標準正交,但方陣
的行向量確實是標準正交,但方陣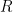 的主對角包含零元。
的主對角包含零元。
當
老師 您所貼的這個程式 是否有問題
A 矩陣 第一行與第二行 均為1 1 0
Q之第一行應該為 A之第一行的單位向量
但程式跑出來確是加負號
這個答案是正確的,Q向量的方向不必與A相同。電腦程式未必使用Gram-Schmidt正交化程序,還有其他算法比較穩定。
感謝老師
matlab的QR分解 跟這個程式的QR分解所得到答案不同
如 A:3*2 利用matlab所計算出來的Q為3*3 但網頁所算出來為3*2
是否代表QR分解 有兩種定義
另外台聯大線代 官方公佈解答
他所說的QR分解的前題 都已經限定行獨立 如103台聯大B
他有一題 官方公佈解答的前題已經為行獨立 但題目並沒有說
這樣回使得答案不同
其實有點無所適從
QR 分解有兩種形式,請參考下文:
感謝老師 詳述QR分解的兩種定義
其實在看台聯大線代題目 遇到QR分解的時候 都會怕怕的 因為題目並不會說明是那一種定義
如103台聯大B卷 選擇題裡面 敘述說 A為m by n 且A=QR 其中Q為orthogonal matrix R為上三角矩陣
他的a選項說 m大約等於n
我的想法是 R為上三角 而依上三角矩陣的定義 他為方陣 且主對角線均不為0 所以Q與R均可逆 故A可逆且A為方陣
所以m應該跟n相等
但公佈解答確有a
請問老師 我這樣思考是否正確
你說的問題是這個嗎? be (
be ( ) matrix, which can be factored into a matrix-product
) matrix, which can be factored into a matrix-product  , where
, where 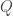 is an orthogonal matrix and
is an orthogonal matrix and 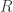 is an upper triangular matrix. Which of the following statements are true?
is an upper triangular matrix. Which of the following statements are true?
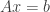 must be a consistent system for any vector
must be a consistent system for any vector  .
. contains only the all-zero vector.
contains only the all-zero vector. , then
, then  is diagonalizable.
is diagonalizable.
Let
a)
b) The system of linear equations
c) The right null space of
d) If
e) None of the above are true.
如果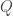 是正交矩陣,則
是正交矩陣,則 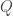 是方陣;
是方陣;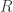 是上三角矩陣,則
是上三角矩陣,則 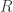 也是方陣。因此,
也是方陣。因此, ,故(a)是對的。如果
,故(a)是對的。如果  ,我說
,我說 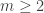 也沒錯,是吧?
也沒錯,是吧?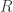 是可逆的,故(b)是錯的。
是可逆的,故(b)是錯的。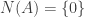 ,即
,即  是可逆的,這未必成立,(c)是錯的。
是可逆的,這未必成立,(c)是錯的。 可對角化,當然不總是成立,(d)是錯的。
可對角化,當然不總是成立,(d)是錯的。
因為沒有指明
(c)說
(d)說
這裏做個修正 R為上三角 但不一定可逆 但Q R均為方陣
謝謝老師 您解決了我 想了很久的問題 非常非常感激您
我看不出這個問題的涵義,到底是考正交矩陣、上三角矩陣的定義,還是問QR分解的性質?四個選項東拉西扯,跟QR分解完全無關。台聯大考題總是有個自保選項:None of the above are true. 題目出錯了沒答案也無妨。
因為這題公佈解答為 a c
所以觀念上有點亂
知道正確答案為a 那解決了一些觀念上的問題
因為我是由答案去反推它的題目 才會說這題A為行獨立
然後才會推出一些錯誤觀念
再次謝謝老師 台灣若能多一些像您這樣的老師 學子讀線代將會更有動力
如果問題改成這樣那麼選項a,c是正確的: be (
be ( ) matrix, which can be factored into a matrix-product
) matrix, which can be factored into a matrix-product  , where
, where 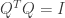 and
and 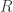 is a nonsingular upper triangular matrix. Which of the following statements are true?
is a nonsingular upper triangular matrix. Which of the following statements are true?
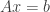 must be a consistent system for any vector
must be a consistent system for any vector  .
. , then A is diagonalizable.
, then A is diagonalizable.
Let
a)
b) The system of linear equations
c) The right null space of A contains only the all-zero vector.
d) If
e) None of the above are true.
我對線代蠻有興趣一直以來有空就是拜讀老師部落格
因為台聯線代都會公佈解答
所以會對自己測驗一下
其實這題當年在看的時候就覺得很怪 這幾天偶然又看到老師這篇文章 斗膽請教
沒想到老師回答如此詳細
學生內心是很感動的 看了很多線代的書 有時候困惑的是名詞定義問題
很遺憾學生時代沒能遇到您
祝老師新年快樂
若A的行向量為線性相關, 如老師舉的這題, 利用Gram-Schmidt正交化程序,
其實也是無法得到答案的, 代入公式後第二個向量會是零向量, 此時只能任取跟第一個向量正交的向量當成Q之第二個向量, 所以電腦程式跑出來的才是如此
感謝老師提點
我改成
Q之行向量必定為標準正交
transpose Q*Q=I
R不一定為上三角
但R之 aij =0 , i>j. aij>=0 ,i<j
若Ax=b 無解且A是mxn矩陣,A的columns 是線性獨立時
如果用QR分解代入方程式去做
即 QRx=b
=> (transpose Q)*QRx=( transpose Q)*b (等號兩邊同乘Q的轉置)
Rx=(transpose Q)* b
x=(R的反矩陣)*(transpose Q) * b 唯ㄧ解 (R是upper triangular matrix 對角線元素必為正數 所以必定可逆)
問題: “無解”的線性方程組Ax=b 卻 解出答案!!
為何???
我的想法是
第一步無法逆推!
所以 QRx=b 與 (transpose Q)*QRx=( transpose Q)*b
的solution set 是不同
後者的解集合包含於前者的解集合
故依此方式解出來的x 不是原方程組Ax=b的解
而是least square solution
你的推論是正確的。
 同義於
同義於 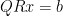 ,但
,但 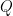 不一定是一個方陣,因此
不一定是一個方陣,因此  與
與  有不同的解,除非
有不同的解,除非  可逆。
可逆。
你已經指出 的解就是最小平方解。請參考下文:
的解就是最小平方解。請參考下文: