Strassen 演算法──分治矩陣乘法

本文的閱讀等級：初級

令 $A=[a_{ij}]$ 和 $B=[b_{ij}]$ 為 $n\times n$ 階矩陣。矩陣乘積 $C=AB$ 需要使用多少乘法與加法運算？根據矩陣乘法定義，

$\displaystyle c_{ij}=\sum_{k=1}^na_{ik}b_{kj},~~i=1,\ldots,n,~~j=1,\ldots,n$ 。

因為 $n\times n$ 階矩陣 $C$ 有 $n^2$ 個元，計算每一元需要 $n$ 個乘法和 $(n-1)$ 個加法，故知 $n\times n$ 階矩陣乘積共使用了 $n^3$ 個乘法和 $n^3-n^2$ 個加法。長久以來，人們普遍認為矩陣乘法定義本身即為最佳的算法，這個迷思直到1969年才被施特拉森^[1](Volker Strassen) 打破──他提出了一個更快捷的分治 (divide-and-conquer) 矩陣乘法，稱為 Strassen 演算法。

考慮 $2\times 2$ 階分塊矩陣乘法

$\displaystyle \begin{bmatrix} C_{11}&C_{12}\\ C_{21}&C_{22} \end{bmatrix}=\begin{bmatrix} A_{11}&A_{12}\\ A_{21}&A_{22} \end{bmatrix}\begin{bmatrix} B_{11}&B_{12}\\ B_{21}&B_{22} \end{bmatrix}$ ，

其中每一分塊皆為方陣。傳統的矩陣乘法運算方式， $C_{ij}=A_{i1}B_{1j}+A_{i2}B_{2j}$ ，總共使用8個分塊乘法和4個分塊加法。Strassen 演算法使用7個分塊乘法和18個分塊加法，如下：

$\displaystyle\begin{aligned} P_1&=(A_{11}+A_{22})(B_{11}+B_{22})\\ P_2&=(A_{21}+A_{22})B_{11}\\ P_3&=A_{11}(B_{12}-B_{22})\\ P_4&=A_{22}(B_{21}-B_{11})\\ P_5&=(A_{11}+A_{12})B_{22}\\ P_6&=(A_{21}-A_{11})(B_{11}+B_{12})\\ P_7&=(A_{12}-A_{22})(B_{21}+B_{22})\\ C_{11}&=P_1+P_4-P_5+P_7\\ C_{12}&=P_3+P_5\\ C_{21}&=P_2+P_4\\ C_{22}&=P_1+P_3-P_2+P_6. \end{aligned}$

直接代入化簡即可驗證上述公式的正確性。假設 $n=2m$ ，上面所有分塊皆為 $m\times m$ 階。傳統的矩陣乘法使用了 $8m^3$ 個乘法和 $8m^3-4m^2$ 個加法。如果 Strassen 演算法僅執行至分塊等級，也就是說， $m\times m$ 階分塊乘法仍採用傳統方法計算，則7次分塊乘法共使用 $7m^3$ 個乘法和 $7(m^3-m^2)$ 個加法，再加上18次分塊加法使用的 $18m^2$ 個加法，總計是 $7m^3$ 個乘法和 $7m^3+11m^2$ 個加法。若 $m\gg 1$ ，不論乘法或加法，Strassen 演算法僅耗費傳統方法 7/8 的計算量。

我們可以繼續應用 Strassen 演算法於 $m\times m$ 階矩陣 $P_i$ 涉及的乘法運算。若 $n=2^k$ ，運用遞歸方式可達成分治效果。令 $m(k)$ 代表計算 $2^k\times 2^k$ 階矩陣乘積所耗用的乘法總數。因為

$\displaystyle m(k)=7m(k-1)$ ，

且 $m(0)=1$ (對應 $1\times 1$ 階純量乘法)，可得

$m(k)=7^k=2^{k\log_27}=n^{\log_27}\approx n^{2.807}$ 。

令 $a(k)$ 表示 Strassen 算法應用於 $2^k\times 2^k$ 階矩陣乘法使用的加法總數。由前述分析可知 $a(k)$ 包含7次 $2^{k-1}\times 2^{k-1}$ 階矩陣乘法使用的 $7a(k-1)$ 個加法，以及18次 $2^{k-1}\times 2^{k-1}$ 階矩陣加法所需的 $18(2^{k-1})^2$ 個加法，即

$\displaystyle a(k)=7a(k-1)+18(2^{k-1})^2=7a(k-1)+\frac{9}{2}\cdot 4^k$ 。

上式通除以 $7^k$ ，

$\displaystyle 7^{-k}a(k)=7^{-(k-1)}a(k-1)+\frac{9}{2}\left(\frac{4}{7}\right)^k$ 。

因為 $a(0)=0$ ( $1\times 1$ 階純量乘法未使用加法)，

$\displaystyle 7^{-k}a(k)=\frac{9}{2}\sum_{j=1}^k\left(\frac{4}{7}\right)^j<\frac{9}{2}\cdot\frac{4}{3}=6$ 。

所以 Strassen 演算法的加法總量是

$\displaystyle a(k)\le 6\cdot 7^k=6n^{\log_27}\approx 6n^{2.807}$ 。

在實際應用時，若 $n$ 不等於 $2$ 的冪，可將 $A$ 和 $B$ 擴充為 $\begin{bmatrix} A&0\\ 0&I \end{bmatrix}$ 和 $\begin{bmatrix} B&0\\ 0&I \end{bmatrix}$ 。不過此舉勢必引入額外的計算量與儲存量。根據2000年的硬體架構，矩陣尺寸必須超過1,000，Strassen 演算法才可能擊敗經過高度優化的傳統算法。即便矩陣尺寸增大至10,000，相較於傳統算法，Strassen 演算法所能提昇的運算效率依然十分有限 (約小於10%)^[2]。

Strassen 演算法的推導

考慮 $2\times 2$ 階矩陣乘法

$\displaystyle \begin{bmatrix} w&x\\ y&z \end{bmatrix}=\begin{bmatrix} a&b\\ c&d \end{bmatrix}\begin{bmatrix} p&q\\ r&s \end{bmatrix}$ 。

乘開上式，

$\displaystyle\begin{aligned} w&=ap+br\\ y&=cp+dr\\ x&=aq+bs\\ z&=cq+ds, \end{aligned}$

將這四個式子合併成矩陣表達式

$\displaystyle \begin{bmatrix} w\\ y\\ x\\ z \end{bmatrix}=\begin{bmatrix} a&b&0&0\\ c&d&0&0\\ 0&0&a&b\\ 0&0&c&d \end{bmatrix}\begin{bmatrix} p\\ r\\ q\\ s \end{bmatrix}$ 。

我們的任務要將上式的 $4\times 4$ 階矩陣分解成數個矩陣之和以期減少乘法運算。分解出來的矩陣至多僅含4個非零元，且所有非零元都位於一 $2\times 2$ 階子陣，例如，

$\displaystyle \begin{bmatrix} \ast&\ast&0&0\\ \ast&\ast&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix},~~\begin{bmatrix} 0&0&0&0\\ \ast&0&\ast&0\\ 0&0&0&0\\ \ast&0&\ast&0 \end{bmatrix},~~\begin{bmatrix} \ast&0&0&\ast\\ 0&0&0&0\\ 0&0&0&0\\ \ast&0&0&\ast \end{bmatrix}$ 。

考慮下列三種分解型態：
(1) 型態I：子陣有相同的元，需要1個乘法運算，如

$\displaystyle \begin{bmatrix} a&a\\ a&a \end{bmatrix}\begin{bmatrix} u\\ v \end{bmatrix}=\begin{bmatrix} a(u+v)\\ a(u+v) \end{bmatrix}$ 。

(2) 型態II：子陣的元有相同的絕對值，但兩行或兩列不同號，需要1個乘法運算，如

$\displaystyle \begin{bmatrix} a&-a\\ a&-a \end{bmatrix}\begin{bmatrix} u\\ v \end{bmatrix}=\begin{bmatrix} a(u-v)\\ a(u-v) \end{bmatrix}$ 。

(3) 型態III：子陣為上或下三角矩陣，且 (非零) 非主對角元等於兩主對角元之差，這時需要2個乘法運算，如

$\displaystyle \begin{bmatrix} a&0\\ a-b&b \end{bmatrix}\begin{bmatrix} u\\ v \end{bmatrix}=\begin{bmatrix} au\\ au+b(v-u) \end{bmatrix}$ ，

型態III可分解為兩個退化的型態I和型態II (所謂退化是指存在零行或零列)，如

$\displaystyle \begin{bmatrix} a&0\\ a-b&b \end{bmatrix}=\begin{bmatrix} a&0\\ a&0 \end{bmatrix}+\left[\!\!\begin{array}{rc} 0&0\\ -b&b \end{array}\!\!\right]$ 。

以下是詳細的分解步驟：設法製造型態I和型態II，可能的方式很多，下為一例：

$\displaystyle \begin{bmatrix} a&b&0&0\\ c&d&0&0\\ 0&0&a&b\\ 0&0&c&d \end{bmatrix}=\left[\!\!\begin{array}{rccr} -d&d&0&0\\ -d&d&0&0\\ 0&0&a&-a\\ 0&0&a&-a \end{array}\!\!\right]+\begin{bmatrix} a+d&b-d&0&0\\ c+d&0&0&0\\ 0&0&0&a+b\\ 0&0&c-a&a+d \end{bmatrix}$ 。

令 $M_1$ 表示上式等號右邊的第二個矩陣。觀察發現 $(M_1)_{11}=(M_1)_{44}=a+d$ ，故可繼續製造型態I，如下：

$\displaystyle M_1=\begin{bmatrix} a+d&0&0&a+d\\ 0&0&0&0\\ 0&0&0&0\\ a+d&0&0&a+d \end{bmatrix}+\begin{bmatrix} 0&b-d&0&-(a+d)\\ c+d&0&0&0\\ 0&0&0&a+b\\ -(a+d)&0&c-a&0 \end{bmatrix}$ 。

令 $M_2$ 表示上式等號右邊的第二個矩陣。觀察發現 $M_2$ 可分解成兩個型態III：

$\displaystyle M_2=\begin{bmatrix} 0&0&0&0\\ c+d&0&0&0\\ 0&0&0&0\\ (c-a)-(c+d)&0&c-a&0 \end{bmatrix}+\begin{bmatrix} 0&b-d&0&(b-d)-(a+b)\\ 0&0&0&0\\ 0&0&0&a+b\\ 0&0&0&0 \end{bmatrix}$ 。

分離等號右邊兩矩陣的相異元，各自可分解成兩個退化型態I和型態II。最後，整理所有的分解矩陣，按照 Strassen 演算法給定的排序，即有

$\displaystyle\begin{aligned} \begin{bmatrix} a&b&0&0\\ c&d&0&0\\ 0&0&a&b\\ 0&0&c&d \end{bmatrix}&=\begin{bmatrix} a+d&0&0&a+d\\ 0&0&0&0\\ 0&0&0&0\\ a+d&0&0&a+d \end{bmatrix}+\begin{bmatrix} 0&0&0&0\\ c+d&0&0&0\\ 0&0&0&0\\ -(c+d)&0&0&0 \end{bmatrix}\\ &+\left[\!\!\begin{array}{rccr} 0&0&0&0\\ 0&0&0&0\\ 0&0&a&-a\\ 0&0&a&-a \end{array}\!\!\right]+\left[\!\!\begin{array}{rccr} -d&d&0&0\\ -d&d&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{array}\!\!\right]\\ &+\begin{bmatrix} 0&0&0&-(a+b)\\ 0&0&0&0\\ 0&0&0&a+b\\ 0&0&0&0 \end{bmatrix}+\begin{bmatrix} 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ c-a&0&c-a&0 \end{bmatrix}\\ &+\begin{bmatrix} 0&b-d&0&b-d\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix}. \end{aligned}$

上式也可以表示為「行列展開」的矩陣乘法：

$\displaystyle\begin{aligned} \begin{bmatrix} a&b&0&0\\ c&d&0&0\\ 0&0&a&b\\ 0&0&c&d \end{bmatrix}&=\begin{bmatrix} 1\\ 0\\ 0\\ 1 \end{bmatrix}(a+d)\begin{bmatrix} 1&0&0&1 \end{bmatrix}+\left[\!\!\begin{array}{r} 0\\ 1\\ 0\\ -1 \end{array}\!\!\right](c+d)\begin{bmatrix} 1&0&0&0 \end{bmatrix}\\ &+\left[\!\!\begin{array}{c} 0\\ 0\\ 1\\ 1 \end{array}\!\!\right](a)\begin{bmatrix} 0&0&1&-1 \end{bmatrix}+\left[\!\!\begin{array}{c} 1\\ 1\\ 0\\ 0 \end{array}\!\!\right](d)\begin{bmatrix} -1&1&0&0 \end{bmatrix}\\ &+\left[\!\!\begin{array}{r} -1\\ 0\\ 1\\ 0 \end{array}\!\!\right](a+b)\begin{bmatrix} 0&0&0&1 \end{bmatrix}+\left[\!\!\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\!\!\right](c-a)\begin{bmatrix} 1&0&1&0 \end{bmatrix}\\ &+\left[\!\!\begin{array}{c} 1\\ 0\\ 0\\ 0 \end{array}\!\!\right](b-d)\begin{bmatrix} 0&1&0&1 \end{bmatrix}. \end{aligned}$

原始的 $4\times 4$ 階矩陣分解成7個型態I或形態II (包含退化情形)，所以共使用7個乘法運算。

參考來源：
[1] 維基百科：Volker Strassen
[2] 維基百科：Strassen algorithm

7 Responses to Strassen 演算法──分治矩陣乘法

張盛東 says:

06/04/2013 at 11:54 pm

有時候真的很敬佩發明這個算法的人，到底是怎么發現Strassen 演算法所使用的那7個分塊乘法和18個分塊加法？
另外，老師能否介紹一下其他比strassen更好的算法？

- ccjou says:
  
  06/05/2013 at 8:40 am
  
  我猜想你說的更好算法是Coppersmith–Winograd algorithm。它的漸近分析效率是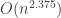 $O(n^{2.375})$ ，不過此法僅有理論價值但不具實用性，因為目前的電腦無法計算超大矩陣乘法。CW算法建立在tensor product，請參見下文介紹：
  
  Click to access matrixmult.pdf
  
ccjou says:

06/05/2013 at 5:15 pm

稍後我再將Strassen 演算法的推演過程補上來。

- SN says:
  
  04/21/2016 at 8:55 pm
  
  所以您打算貼了嗎?
  
  - ccjou says:
    
    04/21/2016 at 9:47 pm
    
    你問的有點晚了。如果我記得不錯，2013年6月6日便將推演過程貼上，粗體標題 Strassen 演算法的推導以下即是。
    
jianglong says:

05/14/2024 at 5:23 pm

Strassen 演算法使用7個分塊乘法和18個分塊加法

是不是应该为：

Strassen 演算法使用7個分塊乘法和8個分塊加法

18 -> 8

- jianglong says:
  
  05/14/2024 at 7:39 pm
  
  请忽略~

	jianglong on Strassen 演算法──分治矩陣乘法
	jianglong on Strassen 演算法──分治矩陣乘法
	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明