歐幾里得空間的數學結構

Posted on 09/04/2015 by ccjou

本文的閱讀等級：中級

歐幾里得空間 $\mathbb{R}^n$ 是有序數組 (稱為點或向量) $(x_1,\ldots,x_n)$ 形成的集合，其中 $x_i$ 為實數。在歐氏幾何中，譬如平面幾何與空間幾何，我們可以計算兩點之間的距離、多個向量的線性組合 (向量加法與純量乘法)、向量的長度，以及兩個向量之間的夾角。數學家將這些概念予以抽象化，並用公設化方式定義出不同的數學結構，稱為空間。在數學中，空間一詞並不單獨存在，我們可以稱 $X$ 是一個集合，但不講 $X$ 是一個空間。粗淺地說，空間是一個賦予某種數學結構的集合，該數學結構決定空間的名稱，例如線性代數讀者熟悉的向量空間。本文概述歐氏空間 $\mathbb{R}^n$ 的一些數學結構，背後的目的是將有限維空間延伸至無限維空間，其中最重要的一個特例是希爾伯特 (Hilbert) 空間。

度量空間

度量空間 (賦距空間，metric space) 是一個集合 (一般是非空集合)，並賦予一距離函數，稱為度量 (度規，metric)。具體而言，度量空間是一個二元組 $(X,d)$ ，其中 $X$ 為集合，度量 $d:X\times X\to[0,\infty)$ 為非負函數，滿足

(M1) $d(x,y)\ge 0$ (非負性)
(M2) $d(x,y)=0\Leftrightarrow x=y$ (不可區分者的同一性)
(M3) $d(x,y)=d(y,x)$ (對稱性)
(M4) $d(x,z)\le d(x,y)+d(y,z)$ (三角不等式)

公理 (M4)是歐幾里得幾何中三角不等式的抽象公式化，這是一個非常重要的定義性質。度量空間的四個公理並不獨立，(M1) 可由其他三個公理推得：

$2d(x,y)=d(x,y)+d(y,x)\ge d(x,x)=0$ 。

給定集合 $X$ ，度量 $d$ 有許多合法的定義。例如，考慮 $X=\mathbb{R}^n$ 的兩點 $x=(x_1,\ldots,x_n)$ 和 $y=(y_1,\ldots,y_n)$ ，歐氏距離

$\displaystyle d_2(x,y)=\left(\sum_{i=1}^n(x_i-y_i)^2\right)^{1/2}$

或曼哈頓距離 (Manhattan distance)

$\displaystyle d_1(x,y)=\sum_{i=1}^n\vert x_i-y_i\vert$

皆為集合 $X$ 上的度量 (請讀者自行驗證 $d_2$ 和 $d_1$ 滿足上述公理)。因此，即便 $(X,d_2)$ 和 $(X,d_1)$ 有相同的底層集 (underlying set) $X$ ，兩者是不同的度量空間。事實上，給定一個非空集合 $X$ ，存在無限多個度量空間。譬如，若 $d$ 是定義於 $X$ 的一個度量，則 $d_\alpha(x,y)=\alpha d(x,y)$ ， $\alpha>0$ ，也是在 $X$ 上的度量。

度量空間的核心概念在於賦予集合的元素之間距離或鄰近性，稱之為拓撲結構 (度量空間是一個拓撲空間)。分析學中映射的連續性與序列的收斂性可以放在度量空間上討論。令 $f:X\to Y$ 為一個從度量空間 $(X,d_1)$ 至 $(Y,d_2)$ 的映射。我們說 $f$ 在點 $x_0\in X$ 是連續的，若對於每一 $\epsilon>0$ ，存在一個 $\delta>0$ 使得 $d_1(x_0,x)<\delta$ 蘊含 $d_2(f(x_0),f(x))<\epsilon$ 。映射 $f$ 的連續性由兩個度量空間 $(X,d_1)$ 和 $(Y,d_2)$ 共同決定。如果 $f$ 在每一 $x_0\in X$ 都是連續的，則稱 $f$ 是一個連續映射。在度量空間 $(X,d)$ ，我們說 $\{x_n\}=\{x_1,x_2,\ldots,\}$ 是一個收斂序列，如果有一點 $x_0\in X$ ，對於每一 $\epsilon>0$ ，存在一正整數 $N$ ，使得 $n\ge N$ 蘊含 $d(x_0,x_n)<\epsilon$ 。換一個說法，若 $\{d(x_0,x_n)\}$ 收斂至 $0$ ，則 $\{x_n\}$ 是收斂序列。點 $x_0$ 稱為序列 $\{x_n\}$ 的極限 (limit)。請注意，一個收斂序列的極限是唯一的，記為 $\displaystyle\lim_{n\to\infty}x_n=x_0$ 或 $x_n\to x_0$ 。假設 $x_n\to x_0$ 且 $x_n\to y_0$ ，則

$\displaystyle d(x_0,y_0)\le d(x_0,x_n)+d(x_n,y_0)=d(x_0,x_n)+d(y_0,x_n)\to 0$ ，

故 $x_0=y_0$ 。表面上，連續與收斂是不同的概念，但兩者其實有密切的關係。下面是等價的陳述：

映射 $f$ 在點 $x_0$ 是連續的；
對於每一收斂序列 $\{x_n\}$ 滿足 $x_n\to x_0$ ， $\displaystyle\lim_{n\to\infty} f(x_n)=f\left(\lim_{n\to\infty} x_n\right)$ 。

接著介紹一個重要的拓撲學概念，叫做完備性 (completeness)。考慮度量空間 $(X,d)$ ，其中 $X=(0,1]$ ， $d$ 是標準度量， $d(x,y)=\vert x-y\vert$ 。明顯地，序列 $\{\frac{1}{n}\}=\{1,\frac{1}{2},\frac{1}{3},\ldots\}$ 被 $X$ 所包含。然而， $\{\frac{1}{n}\}$ 不是一個收斂序列，因為極限 $0$ 不屬於 $X$ 。這個現象引領出完備的概念。在度量空間 $(X,d)$ ，我們稱 $\{x_n\}$ 為柯西序列 (Cauchy sequence)，若對於每一 $\epsilon>0$ ，存在正整數 $N$ 使得 $n,m\ge N$ 蘊含 $d(x_n,x_m)\le \epsilon$ 。換句話說， $d(x_n,x_m)\to 0$ 當 $n,m\to\infty$ 。每一個收斂序列都是柯西序列：若 $x_n\to x_0$ ，則

$\displaystyle d(x_n,x_m)\le d(x_n,x_0)+d(x_0,x_m)=d(x_0,x_n)+d(x_0,x_m)\to 0$ 。

上例中， $\{\frac{1}{n}\}$ 是一個柯西序列，但不是於 $(X,d)$ 的收斂序列。這個問題發生的原因在於底層集 $X$ 裡面有一個「洞」，即點 $0$ 。如果將底層集擴充為 $[0,1]=X\cup\{0\}$ ，則每一柯西序列都是收斂序列。針對這個情況，若於一度量空間 $(X,d)$ 的每一柯西序列都存在極限 (也就是收斂序列)，我們稱 $(X,d)$ 是一個完備 (complete) 度量空間。

向量空間

向量空間 (vector space)，或稱線性空間 (linear space)，是一種代數結構，核心概念在於線性組合 (合併向量加法與純量乘法)。我們稱 $\mathcal{V}$ 是一個佈於體 (域，field) $F$ 的向量空間，若 $\mathbf{x},\mathbf{y}\in\mathcal{V}$ 與 $\alpha\in F$ 具備向量加法 $\mathbf{x}+\mathbf{y}$ 和純量乘法 $\alpha\mathbf{x}$ ，並滿足下列公理：

(V1) $\mathbf{x}+\mathbf{y}=\mathbf{y}+\mathbf{x}$ (交換律)
(V2) $\mathbf{x}+(\mathbf{y}+\mathbf{z})=(\mathbf{x}+\mathbf{y})+\mathbf{z}$ (結合律)
(V3) 存在唯一的 $\mathbf{0}\in\mathcal{V}$ 使得 $\mathbf{x}+\mathbf{0}=\mathbf{x}$
(V4) 存在唯一的 $-\mathbf{x}\in\mathcal{V}$ 使得 $\mathbf{x}+(-\mathbf{x})=\mathbf{0}$
(V5) $\alpha(\beta\mathbf{x})=(\alpha\beta)\mathbf{x}$ (結合律)
(V6) $1\mathbf{x}=\mathbf{x}$
(V7) $\alpha(\mathbf{x}+\mathbf{y})=\alpha\mathbf{x}+\alpha\mathbf{y}$ (分配律)
(V8) $(\alpha+\beta)\mathbf{x}=\alpha\mathbf{x}+\beta\mathbf{x}$ (分配律)

若 $F=\mathbb{R}$ ，則 $\mathcal{V}$ 稱為實向量空間；若 $F=\mathbb{C}$ ，則 $\mathcal{V}$ 稱為複向量空間。在線性代數中，歐氏空間 $\mathbb{R}^n$ 是最常見的一個向量空間，其中的元素 $(x_1,\ldots,x_n)$ 構造一個 $n$ 維實向量 $\mathbf{x}$ 。對比連續映射在度量空間扮演重要的角色，線性映射 (變換) 則是向量空間中最重要的運算機制。設 $\mathcal{V}$ 和 $\mathcal{W}$ 為佈於相同數系的向量空間，我們稱 $T:\mathcal{V}\to\mathcal{W}$ 為一個線性映射，若任意 $\mathbf{x},\mathbf{y}\in\mathcal{V}$ 和純量 $\alpha$ 滿足

$\displaystyle\begin{aligned} T(\mathbf{x}+\mathbf{y})&=T(\mathbf{x})+T(\mathbf{y})\\ T(\alpha\mathbf{x})&=\alpha T(\mathbf{x}).\end{aligned}$

線性映射出現在許多科學與工程領域，這是我們對向量空間如此重視的原因。

賦範向量空間

定義於度量空間的連續映射與定義於向量空間的線性映射可以合成為一個連續線性映射，具體的作法是將距離與長度引進向量空間，這個概念稱為範數 (norm)。對於一個佈於體 $F$ 的向量空間 $\mathcal{V}$ ，實函數 $\Vert\mathbf{x}\Vert$ 稱為範數，其中 $\mathbf{x}\in\mathcal{V}$ ，若下列性質成立：

(N1) $\Vert\mathbf{x}\Vert\ge 0$ ， $\Vert\mathbf{x}\Vert=0 \Leftrightarrow\mathbf{x}=\mathbf{0}$ (非負性)
(N2) $\Vert\alpha\mathbf{x}\Vert=\vert\alpha\vert\cdot\Vert\mathbf{x}\Vert$ ， $\alpha\in F$ 是任一純量 (均勻性)
(N3) $\Vert\mathbf{x}+\mathbf{y}\Vert\le\Vert\mathbf{x}\Vert+\Vert\mathbf{y}\Vert$ (三角不等式)

一個賦範向量空間 (normed vector space) 是二元組 $(\mathcal{V},\Vert\cdot\Vert)$ ，其中 $\mathcal{V}$ 是一個向量空間， $\Vert\cdot\Vert$ 是定義於 $\mathcal{V}$ 的一個範數。賦範向量空間 $(\mathcal{V},\Vert\cdot\Vert)$ 是一個度量空間：給定任意 $\mathbf{x},\mathbf{y}\in\mathcal{V}$ ，

$\displaystyle d(\mathbf{x},\mathbf{y})=\Vert\mathbf{x}-\mathbf{y}\Vert$

是定義於 $\mathcal{V}$ 的一個度量。(N1) 表明 $\Vert\mathbf{x}-\mathbf{y}\Vert\ge 0$ ，且 $\Vert\mathbf{x}-\mathbf{y}\Vert=0$ 等價於 $\mathbf{x}=\mathbf{y}$ ，故滿足 (M1) 與 (M2)。設 $\alpha=-1$ ，由 (N2) 可得 $\Vert-(\mathbf{x}-\mathbf{y})\Vert=\Vert\mathbf{x}-\mathbf{y}\Vert$ ，滿足 (M3)。最後，由 (N3) 可得

$\displaystyle \Vert\mathbf{x}-\mathbf{y}\Vert=\Vert\mathbf{x}-\mathbf{z}+\mathbf{z}-\mathbf{y}\Vert\le\Vert\mathbf{x}-\mathbf{z}\Vert+\Vert\mathbf{z}-\mathbf{y}\Vert$ ，

此即 (M4) 的三角不等式。

如果一個賦範向量空間是完備度量空間，則稱之為巴拿赫 (Banach) 空間 (即完備賦範向量空間)。舉例來說，若 $\mathbf{x}=(x_1,\ldots,x_n)\in\mathbb{R}^n$ ，定義向量空間 $\mathbb{R}^n$ 的一個範數，稱為 $p$ ─範數，如下 (見“向量範數”)：

$\displaystyle \Vert\mathbf{x}\Vert_p=\left(\sum_{i=1}^n\vert x_i\vert^p\right)^{1/p}$ ，

其中 $1\le p<\infty$ ，且當 $p=\infty$ ，

$\displaystyle \Vert\mathbf{x}\Vert_\infty=\max_{1\le i\le n}\vert x_i\vert$ 。

對於 $1\le p\le\infty$ ， $(\mathbb{R}^n,\Vert\cdot\Vert_p)$ 是一個巴拿赫空間。如欲將有限維空間 $(\mathbb{R}^n,\Vert\cdot\Vert_p)$ 推廣至無限維空間，我們定義 $l^p$ 為包含所有的序列 $\mathbf{x}=\{x_1,x_2,\ldots\}$ 的集合，並滿足

$\displaystyle \sum_{i=1}^\infty\vert x_i\vert^p<\infty$ ，

其中 $1\le p<\infty$ 。對於 $\mathbf{x}=\{x_n\}\in l^p$ ， $p$ ─範數為

$\displaystyle \Vert\mathbf{x}\Vert_p=\left(\sum_{i=1}^\infty\vert x_i\vert^p\right)^{1/p}$ 。

我們可以證明 $l^p$ 是一個向量空間。因為 $l^p$ 是所有實序列的一個子空間，只要證明若 $\{x_n\},\{y_n\}\in l^p$ 且 $c\in\mathbb{R}$ ，則 $\{x_n+y_n\}\in l^p$ 且 $\{cx_n\}\in l^p$ 。使用 Minkowski 不等式 (見“向量範數”)，令 $n\to\infty$ ，

$\displaystyle \left(\sum_{i=1}^\infty\vert x_i+y_i\vert^p\right)^{1/p}\le \left(\sum_{i=1}^\infty\vert x_i\vert^p\right)^{1/p}+\left(\sum_{i=1}^\infty\vert y_i\vert^p\right)^{1/p}<\infty$ ，

以及

$\displaystyle \sum_{i=1}^\infty\vert cx_i\vert^p=\vert c\vert^p\sum_{i=1}^\infty\vert x_i\vert^p<\infty$ 。

在不造成混淆的前提下，我們經常以 $l^p$ 取代二元組 $(l^p,\Vert\cdot\Vert_p)$ 。當 $p=\infty$ ， $l^\infty$ 包含有界序列，範數為

$\displaystyle \Vert\mathbf{x}\Vert_\infty=\sup_{i}\vert x_i\vert$ ，

其中 $\sup$ 是最小上界 (supremum)。對於 $1\le p\le \infty$ ， $l^p$ 是一個巴拿赫空間。

內積空間

我們已經將歐氏幾何中兩點之間的距離、向量的線性組合，以及向量的長度等概念抽象化，最後剩下兩向量之間的夾角，與此相關的概念是內積 (inner product) 和正交 (orthogonality)。令 $\mathcal{V}$ 為複向量空間。內積是一個映射 $\mathcal{V}\times\mathcal{V}\to\mathbb{C}$ ，記為 $\left\langle\mathbf{x},\mathbf{y}\right\rangle$ ，其中 $\mathbf{x},\mathbf{y}\in\mathcal{V}$ ，並滿足下列公理 (見“內積的定義”)：

(I1) $\left\langle\mathbf{x},\mathbf{x}\right\rangle\ge 0$ ， $\left\langle\mathbf{x},\mathbf{x}\right\rangle=0\Leftrightarrow\mathbf{x}=\mathbf{0}$ (非負性)
(I2) $\left\langle\mathbf{x},\mathbf{y}+\mathbf{z}\right\rangle=\left\langle\mathbf{x},\mathbf{y}\right\rangle+\left\langle\mathbf{x},\mathbf{z}\right\rangle$ (可加性)
(I3) $\left\langle\mathbf{x},\alpha\mathbf{y}\right\rangle=\alpha\left\langle\mathbf{x},\mathbf{y}\right\rangle$ (均勻性)
(I4) $\left\langle\mathbf{x},\mathbf{y}\right\rangle=\overline{\left\langle\mathbf{y},\mathbf{x}\right\rangle}$ (共軛對稱性)

內積空間 (inner product space) 是一個二元組 $(\mathcal{V},\left\langle\cdot,\cdot\right\rangle)$ ，其中 $\mathcal{V}$ 是向量空間， $\left\langle\cdot,\cdot\right\rangle$ 是定義於 $\mathcal{V}$ 的內積。若 $\left\langle\mathbf{x},\mathbf{y}\right\rangle=0$ ，我們說向量 $\mathbf{x}$ 和 $\mathbf{y}$ 是正交的。正交是內積空間中最重要的一個概念，正交使得內積空間擁有完善的幾何性質，例如正交投影。內積空間 $(\mathcal{V},\left\langle\cdot,\cdot\right\rangle)$ 是一個賦範向量空間。我們可以證明

$\displaystyle \Vert\mathbf{x}\Vert=\left\langle\mathbf{x},\mathbf{x}\right\rangle^{1/2}$

是一個範數。不難證明 $\Vert\mathbf{x}\Vert$ 滿足 (N1) 和 (N2)。下面證明 (N3) 三角不等式成立。寫出

$\displaystyle\begin{aligned} \Vert\mathbf{x}+\mathbf{y}\Vert^2&=\left\langle\mathbf{x}+\mathbf{y},\mathbf{x}+\mathbf{y}\right\rangle=\Vert\mathbf{x}\Vert^2+\left\langle\mathbf{x},\mathbf{y}\right\rangle+\left\langle\mathbf{y},\mathbf{x}\right\rangle+\Vert\mathbf{y}\Vert^2\\ &=\Vert\mathbf{x}\Vert^2+2\hbox{Re}(\left\langle\mathbf{x},\mathbf{y}\right\rangle)+\Vert\mathbf{y}\Vert^2\le\Vert\mathbf{x}\Vert^2+2\vert\left\langle\mathbf{x},\mathbf{y}\right\rangle\vert+\Vert\mathbf{y}\Vert^2. \end{aligned}$

使用 Schwarz 不等式 $\vert\left\langle\mathbf{x},\mathbf{y}\right\rangle\vert\le\Vert\mathbf{x}\Vert\cdot\Vert\mathbf{y}\Vert$ (見“Schwarz 不等式”)，可得

$\displaystyle \Vert\mathbf{x}+\mathbf{y}\Vert^2\le\Vert\mathbf{x}\Vert^2+2\Vert\mathbf{x}\Vert\cdot\Vert\mathbf{y}\Vert+\Vert\mathbf{y}\Vert^2=(\Vert\mathbf{x}\Vert+\Vert\mathbf{y}\Vert)^2$ 。

如果一內積空間是完備度量空間，則稱之為希爾伯特空間 (即完備內積空間)。因此，希爾伯特空間是定義了內積的巴拿赫空間。歐氏空間 $\mathbb{R}^n$ 與空間 $l_2$ 都是希爾伯特空間。在歐氏空間 $\mathbb{R}^n$ ，向量 $\mathbf{x}=(x_1,\ldots,x_n)$ 和 $\mathbf{y}=(y_1,\ldots,y_n)$ 的內積定義如下：

$\displaystyle \left\langle\mathbf{x},\mathbf{y}\right\rangle=\sum_{i=1}^nx_iy_i$ 。

在 (實) 空間 $l_2$ ，向量 (序列) $\mathbf{x}=\{x_1,x_2,\ldots\}$ 和 $\mathbf{y}=\{y_1,y_2,\ldots\}$ 的內積為

$\displaystyle \left\langle\mathbf{x},\mathbf{y}\right\rangle=\sum_{i=1}^\infty x_iy_i$ 。

據此，我們可以將空間 $l_2$ 視為無限維歐氏空間，前提是每一 $\mathbf{x}=\{x_1,x_2,\ldots\}\in l_2$ 滿足 $\Vert\mathbf{x}\Vert_2^2=\sum_{i=1}^\infty \vert x_i\vert^2<\infty$ (見“從幾何向量空間到函數空間”)。

最後我用一張圖呈現歐氏空間 $\mathbb{R}^n$ 的數學結構階層關係，X空間 $\to$ Y空間表示X空間蘊含Y空間，各空間的核心概念總結於下：

度量空間：度量 (距離)
向量空間：線性組合
賦範向量空間：範數 (長度)
巴拿赫空間：範數與完備性
內積空間：內積 (角度)
希爾伯特空間：內積與完備性

歐幾里得空間的數學結構關係圖

This entry was posted in 希爾伯特空間 and tagged 賦範向量空間, lp空間, 內積空間, 向量空間, 完備性, 巴拿赫空間, 希爾伯特空間, 度量空間, 柯西序列. Bookmark the permalink.

19 Responses to 歐幾里得空間的數學結構

Li says:

02/29/2016 at 10:33 am

老師您好: 最近剛開始接觸數學上各式各樣的空間，感謝您的這篇網誌的詳細解釋。我有兩個問題想請教您，先謝謝您的回答。

1. 請問定義這些特殊結構(metric, norm, dot product)的目的為何? 他們的實用性在哪裡?
以賦範向量空間為例，我的理解是在這個空間的元素(vector)都要滿足(V1)-(V8)，然後對每個元素能夠計算其長度(norm)。所以其實就是原本向量空間多了長度的概念。但是我不清楚為這樣有什麼特別的好處?

2. 想要請教如何理解空間中”連續”的概念。我查了維基百科，但是還是不是很明白。裡面提到在拓樸空間可以定義連續的概念，而賦範向量空間同時是拓樸空間和向量空間。請問要怎麼理解賦範向量空間中的連續的概念? 能否想像是在集合中的某些元素距離非常近呢?

謝謝!

Reply
- ccjou says:
  
  02/29/2016 at 12:30 pm
  
  正巧我還在寫賦範向量空間的介紹，近期內會貼上來，這裡先簡單回覆：我們想將有限維向量空間(線性代數)推廣至無限維向量空間。但一般的無限維向量空間太大，我們所能處理的無限維向量空間叫Hilbert 空間(應用最廣的一種)，下文最末一段粗略地提到為什麼要度量範數：
  
  無限維向量空間的基底
  
  連續與收斂有關(如上文)，在無限維向量空間(或分析學)中收斂是一個很重要的概念，欲證明存在一個向量具有某些性質，我們常建立一個適當的向量序列收斂至一極限，而此極限可以被證明滿足該性質。
  
  Reply
- ccjou says:
  
  04/12/2016 at 12:20 pm
  
  針對你的提問寫了賦範向量空間的介紹，請參閱下文：
  
  賦範向量空間
  
  Reply
Noname says:

05/28/2016 at 6:24 am

請問一下，就我所知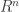 $R^n$ 好像是指純集合，應該不能稱為歐基里德空間？
另請問歐基里德空間的真正定義是什麼呢？

Reply
- ccjou says:
  
  05/28/2016 at 11:54 am
  
  https://en.m.wikipedia.org/wiki/Euclidean_space
  請參閱維基百科解釋
  
  Reply
  - Noname says:
    
    05/28/2016 at 12:48 pm
    
    謝謝回答，我有查過維基的解釋，但還是不甚清楚，所以才來這邊詢問。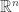
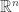    是說 $\mathbb{R}^n$ 上定義了inner product $latex $，就可以把 $(\mathbb{R}^n,)$ 稱為歐基里德空間嗎？還是不一定要在 $\mathbb{R}^n$ ，只要所有的inner product space都算是歐基里德空間?
    
    Reply
    - Noname says:
      
      05/28/2016 at 12:54 pm
      
      謝謝回答，我有查過維基的解釋，但還是不甚清楚，所以才來這邊詢問。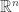
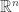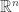      是說 $\mathbb{R}^n$ 上定義了inner product: ，就可以把( $\mathbb{R}^n$ , )稱為歐基里德空間嗎？那這樣要把distance, angle的定義都一併定義出來，才能算是歐基里德空間嗎？如果只單純註明說是( $\mathbb{R}^n$ , )？
      另外是否不一定要在 $\mathbb{R}^n$ ，只要所有的inner product space都算是歐基里德空間?
      這個wiki裡有Euclidean structure這個字，可是這個字好像很少人有用，因為我拿去google，貌似沒找到什麼資料
      
      Reply
      - Noname says:
        
        05/28/2016 at 12:54 pm
        
        內積定義的符號(大於小於)我打不出來
        
        Reply
      - ccjou says:
        
        05/28/2016 at 3:28 pm
        
        請參考下文
        http://www.euclideanspace.com/maths/geometry/space/euclidean/
        
        Reply
Pingback: 歐幾里得空間的數學結構 | 不分享空間
ROBOT1018 says:

04/12/2017 at 5:38 pm

老師我想請問一下對於巴拿赫空間、完備賦範向量空間的認知是否可以為如下：在賦範向量空間(V,norm)中，對於定義出的p norm存在1<=p<=inf，就可以說此賦範向量空間是完備的，即為巴拿赫空間(主要是p norm的定義範圍有關係嗎?因為內文是用p norm來舉例)

但是在度量空間中的完備性概念，是說若每一個柯西序列都是收斂序列、存在著極限，即可以說此度量空間是完備的。度量空間的完備性應該是和賦範向量空間中的完備性指的是同一個東西，不知道要怎麼跟上面提到的p norm觀念來做結合?

而對於賦範向量空間是否完備，將其向量空間從有限維空間推廣至無限維空間，並沒有關係(?)，因為在內文中介紹賦範向量空間提到巴拿赫空間時，是以x={x1,x2,…,xn}來舉例

Reply
- ccjou says:
  
  04/13/2017 at 9:09 am
  
  Click to access ch13.pdf
  
  請參考pp15, Thm13-55
  
  Reply
  - ROBOT1018 says:
    
    04/13/2017 at 10:51 am
    
    謝謝老師，這一章裡面寫得很清楚。不過有一個比較基本的問題想請問一下老師，應該不會跟我上一個人的提問重複到
    
    就是在歐氏空間數學結構圖中可以知道：最上方的R^n是歐式空間，蘊含著希伯爾特空間和巴拿赫空間…等等。但書中寫到說巴拿赫空間是(vector space R^n with lp norm)的二元組，R^n就變成指的是n維實向量空間，是屬於向量空間了。那這樣子跟歐氏空間R^n的概念是不是會有衝突?
    
    Reply
    - ccjou says:
      
      04/13/2017 at 11:10 am
      
      我用R^n表示歐氏空間，又用R^n表示實向量空間，確實會造成一些混淆。不過你應該可以從上下文判斷兩者之間的差異。
      
      Reply
      - ROBOT1018 says:
        
        04/13/2017 at 12:58 pm
        
        OK，謝謝老師的回答。因為學生不是數學本科系出生，很多基礎觀念不是很確定；目前準備攻讀機器人領域和控制理論相關的博班，正在自修重新打造線性代數的觀念。才發現有這麼好的一個地方有這麼多和線性代數相關的資源，而且老師您每天也都會回覆學生的問題，能夠在這裡學習、發問並解開心中的疑惑真的非常幸運!
        
        Reply
        
        ccjou says:
        
        04/13/2017 at 1:06 pm
        
        我也不是數學本科出身。數學其實很簡單，只是我們還沒學會。
Ju-Hsien Lai says:

04/14/2017 at 9:30 am

老師您好!剛剛拜讀完這篇，覺得獲益良多，但有個細節我不太理解想請教您
我理解到內積空間亦為某種度量空間，定義了角度的度量方法，回頭看度量空間公理M2，若度量為0則引出x=y(不可區分者的同一性)，但在內積方法裡則表示二向量是正交的，並非同一個向量，不曉得我的思考裡哪裡出了問題? 先謝謝老師了!

Reply
- ccjou says:
  
  04/14/2017 at 4:30 pm
  
  定義 $d(x,y)=\Vert x-y\Vert$ ，其中 $\Vert{z}\Vert=\left\langle z,z\right\rangle^{1/2}$ 。若 $d(x,y)=0$ ，則 $x-y=0$ ，即 $x=y$ 。
  
  Reply
Brian-Su says:

11/28/2020 at 3:19 pm

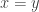要如何說明Rn is a Hilbert space with an inner product?

Reply

	jianglong on Strassen 演算法──分治矩陣乘法
	jianglong on Strassen 演算法──分治矩陣乘法
	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明