本文的閱讀等級:中級
在線性代數的發展過程中,設計效率高且穩定性佳的矩陣特徵值算法是一個非常重要的研究問題。給定一個 階方陣
,特徵值
和對應的特徵向量
,
,滿足
,或寫為
,因此推論
。表面上,欲決定矩陣
的特徵值
,只需要解出特徵多項式
的根即可。不幸的是,這個方法僅適用於小型矩陣,因為一般
次方程式並不存在公式解。針對高次多項式,雖然確實有可用的迭代 (iteration) 求根算法,然而,求多項式根在本質上是一個病態問題,也就是說,根的位置很容易受到多項式係數的微小擾動而發生劇烈改變。Wilkinson 多項式說明了這種情況,考慮
當 的係數從
減小為
,原本一根
改變為
,而
和
兩根則撞擊在一起成為重根
[1]。更有甚者,縱使原本是良置的特徵值問題也可能產生病態多項式,因為這個緣故,我們勢必要尋求其他數值計算方法。本文介紹一個簡易的特徵值算法,稱為 Power 迭代法,以及此法的一個改良版本。
假如方陣 絕對值最大的特徵值唯一存在,
,Power 迭代法的演算程序如下:
Power 迭代法
- 給定一初始向量
- 對於
,直至
收斂止,計算
-
-
Power 迭代法的計算原理建立在差分方程上。當 是可對角化時,存在一組完整的線性獨立特徵向量
對應特徵值
。若
是不可對角化矩陣,只要在
的各個元滲入相當捨入 (roundoff) 誤差的極小隨機擾動量,便能產生微小的特徵值變化,相同特徵值發生的機率也就幾近於零。因此就數值計算而言,所有的矩陣都是可對角化的。既然如此,初始向量可以唯一表示為
,差分方程
的解則為
若 ,亦即初始向量
包含某些成分的
(隨機選擇的
通常滿足上述條件),就有
對於 ,隨著
增大,
逐漸逼近零,得知
。在不失一般性的情況下,假設所有的
皆為單位向量 (unit vector),我們可以推斷以下結果:
數列 將會收斂至絕對值最大的特徵值
,而向量序列
則收斂至對應的特徵向量
。
Power 法的優點是每個計算步驟僅需使用一次矩陣—向量乘法 ;若將正規化特徵向量
的分母改為
,還可以進一步減少計算量。Power 法的收斂速度由比值
決定,如果
十分接近
,這將使得收斂緩慢。此外,Power 法最主要限制在於僅能算出最大特徵值和對應的特徵向量,若要得到其他特徵值和特徵向量,此法還必須加以修改。
Power 迭代法的改良版稱為逆迭代法 (inverse iteration method),或移動逆迭代法 (shift inverse method),它與 Power 法的主要不同處在於以 替換
,詳細演算程序如下:
Power 移動逆迭代法
- 給定一初始向量
- 對於
,直至
收斂止,計算
-
-
-
純量 稱為移動量 (shift),此值決定上述程序最後收斂至那一個特徵值。假設
和所有的特徵值都不相等,而且
與特徵值
的距離最近,可知
,
。由
可推得
,
為
的特徵值。因為
,
是可逆矩陣,故
有特徵值
,對應的特徵向量仍為
。根據 Power 法的結論,當
逐漸增大,
將收斂至絕對值最大的特徵值,亦即
,而
則收斂至特徵向量
。
我們可以由 Gershgorin 圓估計出的特徵值範圍設定鄰近 的一個固定
值 (見“估計特徵值範圍的 Gershgorin 圓”),另一個方法是令
也隨迭代程序靠近
,如下:
還有,計算 並不需要真的得到逆矩陣,解線性方程
即可:計算
的 LU 分解得到
,以正向替代解
,之後再以反向替代解
。
Power 法和逆迭代法的主要應用在於計算大型稀疏矩陣 (包含許多零元) 的特徵值和特徵向量。如果我們想要得到完整的特徵值和特徵向量,或矩陣僅含少數的零元,這時便不宜採用 Power 迭代法。在一般情況下,QR 演算法是目前最常被採用的特徵值算法,這將留待日後再詳細介紹。
引用來源:
[1] http://en.wikipedia.org/wiki/Wilkinson%27s_polynomial

What if the matrix A has several same eigenvalues (for example, A has a Jordan block of (\lambda, 1), (0, \lambda))? What will the convergence rate be?
Let and
and  , where
, where 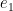 and
and 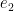 are standard unit vectors. If
are standard unit vectors. If  , the process converges immediately. Consider the case of
, the process converges immediately. Consider the case of  . Then,
. Then,

 ,
,  . The sequence converges sublinearly.
. The sequence converges sublinearly.
As
Note that the power method fails to converge if there are two different dominant eigenvalues with equal absolute value, for example, .
.