本文的閱讀等級:初級
公元1676年,萊布尼茲 (Gottfried Wilhelm Leibniz) 向牛頓 (Isaac Newton) 探詢廣義二項式定理的發現過程。6月13日,牛頓透過英國皇家學會 (The Royal Society) 秘書奧登堡 (Henry Oldenberg) 轉寄回函[1]。在這封信中,牛頓寫出下列無窮級數,並稱之為定理[2]:
牛頓解釋 是所考慮的二項式,
是第一項,
是剩餘項除以
;
可以是整數或分數,為正或負。他舉了一個例子,
對應
,
,
,
[3]。等式右邊的
代表第一項
,
代表第二項
,餘此類推。換句話說,
。從現代人的眼光來看,牛頓描述的公式顯得深奧晦澀。為甚麼
要出現兩次?何不將
寫成
?再來,為甚麼不展開等號右邊各項,列出
的顯式表達?原因無他,牛頓的用意在於簡化計算,稍後將說明。我們要討論的第一個問題,也就是萊布尼茲的疑問:牛頓是怎麼得到這條公式的?

Isaac Newton (1642-1727) From http://www.crystalinks.com/newton.jpg
萊布尼茲收到信之後表示希望瞭解更詳細的訊息,牛頓遂於同年10月24日寄出第二封信。他在信裡闡述自己如何受到沃利斯 (John Wallis) 的內插法啟發而推得適切的公式,甚至透露早在12年前,他身為劍橋大學的大學生即已獲知此法。引領牛頓發現二項式定理的前導問題是為了計算圓周率 。考慮單位圓
所在的第一象限面積,算式如下:
。
牛頓的難題是如何以無窮級數表示 ?跟隨沃利斯的腳步,他考察較為單純的
展開式。當
是正整數時,前面幾個式子為

Gottfried Wilhelm Leibniz (1646-1716) From http://upload.wikimedia.org/wikipedia/commons/6/6a/Gottfried_Wilhelm_von_Leibniz.jpg
作為一個物理學家,牛頓習慣採用實驗歸納法。憑藉直覺,他設想 必定介乎
和
之間,於是列了一張表,將上式的係數抄錄下來,期望通過內插法推得
該列的係數。
牛頓的「不可能的任務」要猜出上表遺漏的部分,這有點像「數獨」(Sudoku) 或「填字遊戲」。先看第一行[4],無疑地,全部常數項的數值應為 。第二行
項的係數呈現等差數列
,意味
中
項的係數應為
。再看第三行
項的係數
,牛頓知道這是三角形數
(見“等差級數和公式的無言證明”),如下圖所示:
第 個三角形數的公式是
,也就是說,
中
項的係數應為
。至此,牛頓沉靜地將數值填入表中:
像多數的數學家一樣,牛頓相信數學的基本形式無所不在。既然常數項是 ,
項的係數是
,
項的係數是
,那麼
項的係數應當為
。代入
,可得
,故
。類似的推論可以持續進行,
中
項的係數為
,
項的係數為
。牛頓將表格填滿,結果如下:
從上表可歸結出
若 為實數,
為整數,定義二項式係數
。
牛頓的二項式展開公式可以用二項式係數表示,今人稱之為廣義二項式定理:
一般所稱的二項式定理專指 為正整數的情況。
牛頓並沒有提出二項式定理的證明。按照歐幾里得的規範,牛頓的二項式定理不能算是一個「定理」,稱作「牛頓猜想」比較恰當。為了鞏固他的「定理」,牛頓舉例申明算式確實成立。譬如,以 取代
,可得
他將上式等號右邊平方,得到
牛頓另舉了其他例子,並宣稱乘開後確認無誤:
牛頓相信有限個項成立的公式可以自動延伸至無限的情況,不過今天的數學家不會認同牛頓處理無窮級數的實驗 (或經驗主義) 手法。即便牛頓論證的邏輯基礎並不穩固,但他的數學直覺與洞察力的確令人激賞。
推廣至一般的二項式 更讓我們見識到牛頓的功力。牛頓從
的展開式觀察出第
項可由第
項算得:
。
雖然牛頓沒有提出證明,但他明瞭 的絕對值應小於
以使無窮級數收斂。假設
,寫出
,並令
,
。在實際應用中,
通常為一分數,故令
。這麼一來,二項式定理可以表示為下列迭代公式:
其中 代表第一項
,
代表第二項
,餘此類推。
牛頓的二項式定理有甚麼實際用途呢?他在信中提及此定理可以簡化開方根的計算。舉例來說,考慮 。改寫為
,將
,
,
,
代入牛頓的定理,計算等號右邊的係數:
使用這四個數值項近似,可得
此近似值與 的誤差為
。相同的技巧可以應用於立方根,四次方根,甚至任何次方根的倒數 (
為負數)。考察上面的計算過程,我們不免感到震驚,原來牛頓的迭代公式的意圖在於套用前一個步驟的結果,故使所需的計算量減至最少。三百多年前,在計算機尚未誕生的時代,牛頓的二項式定理不啻是一個偉大的成就。
註解與來源:
[1] James R. Newman,The World of Mathematics,第一冊,1956,頁519-524。
[2] 牛頓寫出的公式為
其中 就是今日我們使用的
。
[3] 不知道甚麼原因,牛頓經常把平方項 寫成
,譬如
。
[4] 在台灣,橫向稱為列,縱向稱為行。在中國大陸,橫向稱為行,縱向稱為列。


「即便牛頓論證的邏輯基礎並不穩固,但他的數學直覺與洞察力的確令人激賞。」
這句話,很值得深思!
牛頓似乎還有其他「直覺」,在「哲學」領域。
古今中外,還沒得到科學嚴謹證明的某些想法,可能被歸類在「哲學」範疇。
已得到科學詳細證明的部分,很容易歸類在「科學」之中。
然而「科學」與「哲學」,也有共同的部分,能夠與「直覺」對應,也能嚴謹論證。
未來,或許陸續有人作一些聯想,與仔細研究,
循著古人的思考途徑,找尋科學發展的新方向。
牛頓經常把平方項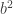 寫成
寫成  ,
,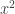 寫成
寫成  。
。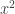 之型式,受到後人學習,
之型式,受到後人學習, ,雖然高斯的年代在歐拉之稍後,然而卻還沒受到歐拉使用符號之影響。
,雖然高斯的年代在歐拉之稍後,然而卻還沒受到歐拉使用符號之影響。
笛卡兒,也是像牛頓這樣寫。
到了歐拉(Euler),使用
大概因為Euler是個著名的人,影響力大,多個數學符號,是由Euler開始造成流行。
高斯也像牛頓那樣寫
(參考書目:《改變世界的17個方程式》第102頁,商周出版)
謝謝你提供的解釋。在牛頓給萊布尼茲的信中,他交互使用 和
和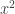 ,前者約占8~9成。我好奇
,前者約占8~9成。我好奇 是否有甚麼特殊的用意,或僅僅是一種習慣而已。
是否有甚麼特殊的用意,或僅僅是一種習慣而已。
Pingback: [生成函數]Formal power series的學習資源 – Catt筆記區
不好意思 這個方法可以推導至虛數的冪次方嗎?
Pingback: 輕鬆談如何教學二項式定理? | 斜槓教師的教育學習網
Pingback: 輕鬆談如何教學二項式定理? – 斜槓教師的教育學習網