本文的閱讀等級:中級
任一 階實矩陣
都可以被分解為
,
稱為極分解 (polar decomposition),其中 是實正交 (orthogonal) 矩陣,
是實對稱半正定 (positive semidefinite) 矩陣。若
是一個複矩陣,則
是么正 (unitary) 矩陣,
是 Hermitian (共軛對稱) 半正定矩陣。
極分解可由奇異值分解推導出 (見“奇異值分解 (SVD)”)。考慮實矩陣 的奇異值分解
。
因為 是一
階矩陣,
,
和
全部都是
階,其中
和
是正交矩陣,
是對角矩陣且主對角元皆不為負。將
插入 SVD,
。
令 且
,則
,其中
是正交矩陣,
是對稱半正定矩陣。直接計算檢查:
。
因為 是對稱半正定,對於任一
,就有
。
當 是可逆時,
的主對角元皆不為零,這時
是正定矩陣。
考慮極分解的行列式
,
其中 等於
或
,因為
。若
是複矩陣,將以上轉置運算
替換成共軛轉置
,則
是么正矩陣,滿足
,且
是 Hermitian 半正定矩陣 (見“從實數系到複數系”)。半正定矩陣
的特徵值不為負 (見“半正定矩陣的判別方法”),故其行列式也不為負 (行列式是特徵值之積),可設
。另外,么正矩陣
的特徵值之絕對值等於
(見“特殊矩陣 (3):么正矩陣 (酉矩陣)”),故可設
,其中
。所以,
。類似複數
的極座標表達式
,
極分解 的半正定矩陣
對應
的絕對值 (或模)
,么正矩陣
對應
的幅角 (或相位)
。
我們也可以寫出反方向的極分解,如下:
。
上式中, 仍為原來的正交 (或么正) 矩陣,利用
,可知
,
則 。
極分解的應用常見於連續介質力學 (continuum mechanics),它將「形變」 分解成「拉伸」和「旋轉」二部分,其中
表示拉伸,
表示旋轉。機器人學的運動學 (kinematics) 分析也使用極分解。令
表示機器手臂各軸微小轉動量所組成之軸座標空間向量,
表示手臂端點於卡氏空間的變動向量,Jacobian 為描述機器手臂各軸轉動率映射至手臂端點之卡氏空間速度的矩陣,此矩陣由軸位置決定故可表示為
,就有
。
考慮手臂端點的變動量
。
機器手臂的靈活度 (manipulability) 由矩陣 決定。對於單位軸變動量,
愈大表示愈靈活,因此有研究者將機器手臂的靈活度定義為 Jacobian 矩陣
的行列式絕對值。下式為
的極分解
:
。
由於 ,且
,所以
。靈活度其實就是
矩陣的特徵值乘積,也等於 Jacobian 矩陣
的奇異值乘積。對於二旋轉軸機器手臂,最大的靈活度發生於二臂夾角為
,這也是人類最常使用的手臂工作狀態 (如圖左)。另一方面,當二臂完全伸長,這時
是不可逆的,故靈活度為
(如圖右)。


老师你好,请问一下’請參見“從實數域到複數域”。’紧接着的下一句的公式是怎么得到的?是后面的那些解释吗?这里有些不明白。。
重讀此文發現確實有幾處推論含糊不清。你現在讀到的是修訂後的版本,如果仍有疑問歡迎再提出來。
周老师,第四行有个小错误,”其中 Q 是么正矩阵”,应该是 U 吧
謝謝指正,我將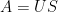 刪除了,這樣簡單些。
刪除了,這樣簡單些。
周老师,请问用newton迭代法如何计算polar decomposition呢?