矩陣與其轉置的相似性

本文的閱讀等級：中級

令 $A$ 為一個 $n\times n$ 階實或複矩陣。轉置矩陣 $A^T$ 與 $A$ 共享許多性質。因為任一 $m\times n$ 階矩陣的行秩等於列秩 (見“行秩=列秩”)，即行空間的維數等於列空間的維數，立知 $\mathrm{rank}A^T=\mathrm{rank}A$ 。再者， $A^T$ 與 $A$ 有相同的行列式值， $\det A^T=\det A$ (見“行列式的運算公式與性質”)。使用行列式性質， $A^T$ 與 $A$ 有相同特徵多項式， $\det(A^T-\lambda I)=\det(A-\lambda I)^T=\det(A-\lambda I)$ ，故 $A^T$ 與 $A$ 有相同的特徵值 (見“每週問題 July 6, 2009”)。

兩個相似矩陣有相同的特徵值 (見“如何檢查兩矩陣是否相似”)，既然 $A^T$ 和 $A$ 有相同的特徵值，我們不免懷疑 $A^T$ 相似於 $A$ ？換句話說，是否存在可逆矩陣 $S$ ，滿足 $A^T=SAS^{-1}$ ？這個問題給人的第一印象似乎並不十分困難，但讀者可能翻遍基礎線性代數課本都找不到答案，原因是證明方法需要引用 Jordan 形式，而 Jordan 形式未必納入基礎線代教材裡。

對於任一 $n\times n$ 階矩陣 $A$ ，存在一個可逆矩陣 $M$ 使得

$J=M^{-1}AM$ ，

其中 $J$ 稱為 Jordan 矩陣或 Jordan 典型形式，是由 Jordan 分塊構成的主對角分塊矩陣 (見“Jordan 典型形式淺說 (上)”)，Jordan 分塊如下：

$\begin{bmatrix} \lambda&1& ~&~\\ ~&\ddots&\ddots&~\\ ~&~&\ddots&1\\ ~&~&~&~\lambda\end{bmatrix}$ 。

例如，

$J=\begin{bmatrix} 8&1&0&0&0\\ 0&8&0&0&0\\ 0&0&3&1&0\\ 0&0&0&3&0\\ 0&0&0&0&3 \end{bmatrix}$

包含 3 個 Jordan 分塊：

$J_1=\begin{bmatrix} 8&1\\ 0&8 \end{bmatrix},~J_2=\begin{bmatrix} 3&1\\ 0&3 \end{bmatrix},~ J_3=\begin{bmatrix} 3\end{bmatrix}$ 。

我們的推理過程需要使用這個性質：任何一個 Jordan 分塊必定與其轉置相似。下面的 $3\times3$ 階矩陣乘法說明了只要將 Jordan 分塊的列與行逆向排序即可得到轉置分塊：

$\begin{bmatrix} 0&0&1\\ 0&1&0\\ 1&0&0 \end{bmatrix}\begin{bmatrix} \lambda&1&0\\ 0&\lambda&1\\ 0&0&\lambda \end{bmatrix}\begin{bmatrix} 0&0&1\\ 0&1&0\\ 1&0&0 \end{bmatrix}=\begin{bmatrix} \lambda&0&0\\ 1&\lambda&0\\ 0&1&\lambda \end{bmatrix}$ 。

對於前面給出的 $5\times 5$ 階 Jordan 矩陣 $J$ ，我們可以設計分塊排列矩陣 (permutation matrix) 實現分塊轉置：

$\begin{bmatrix} 0&1&0&0&0\\ 1&0&0&0&0\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1 \end{bmatrix}\begin{bmatrix} 8&1&0&0&0\\ 0&8&0&0&0\\ 0&0&3&1&0\\ 0&0&0&3&0\\ 0&0&0&0&3 \end{bmatrix}\begin{bmatrix} 0&1&0&0&0\\ 1&0&0&0&0\\ 0&0&0&1&0\\ 0&0&1&0&0\\ 0&0&0&0&1 \end{bmatrix}=\begin{bmatrix} 8&0&0&0&0\\ 1&8&0&0&0\\ 0&0&3&0&0\\ 0&0&1&3&0\\ 0&0&0&0&3 \end{bmatrix}$ ，

因此證明 Jordan 矩陣 $J$ 相似於其轉置 $J^T$ 。

剩下的推導步驟非常簡單。對於 $n\times n$ 階矩陣 $A$ ，若 $A=MJM^{-1}$ 為 Jordan 典型形式， $A$ 相似於 $J$ ，又知道 $J$ 相似於 $J^T$ 。再者，

$A^T=(MJM^{-1})^T=(M^T)^{-1}J^TM^T$ ，

可知 $J^T$ 相似於 $A^T$ 。相似是一種等價關係，故具備傳遞性，推論 $A$ 相似於 $A^T$ 。

反過來說，從 $A$ 與 $A^T$ 的相似關係也可以推論出文初提到的共同性質。因為 $A$ 相似於 $A^T$ ， $A$ 和 $A^T$ 有相同的特徵值， $A$ 和 $A^T$ 的行列式值也相等，因為行列式為特徵值的積。所有的相似變換矩陣都是可逆矩陣，所以 $\hbox{rank}A=\hbox{rank}A^T$ 。

最後我補充一個快捷證明：任一 $n\times n$ 階矩陣 $A$ 可表示為兩個對稱矩陣的積， $A=BC$ ，其中 $B$ 是可逆矩陣 (見“二對稱矩陣分解”)。寫出

$A^T=C^TB^T=CB=B^{-1}BCB=B^{-1}AB$ ，

故存在一個可逆對稱矩陣 $B$ 使得 $A^T=B^{-1}AB$ 。

13 Responses to 矩陣與其轉置的相似性

levinc says:

12/12/2010 at 4:04 am

老師有個小小笨問題請你提點(羞)…
在「對於前面給出的5×5階J，我們設計分塊排列矩陣來實現分塊轉置……」那邊
[0 1 0 0 0;
1 0 0 0 0;
0 0 0 1 0;
0 0 1 0 0;
0 0 0 0 1]
這個排列矩陣是怎麼”看”出來的？還是”算”出來的？還是”刻意選”出來的？　

ccjou says:

12/12/2010 at 6:00 pm

是用肉眼看出來的！

既然每一個 Jordan 分塊可以透過
$P=\begin{bmatrix} 0&\cdots&1\\ ~&\ddots&~\\ 1&\cdots&0 \end{bmatrix}$
排列相似於其轉置，把握「直和」這個結構特性，Jordan 形式
$J=J_1\oplus\cdots\oplus J_k$
也可以透過排列矩陣
$P=P_1\oplus\cdots\oplus P_k$
使得 $J^T=PJP^{-1}=PJP^T=PJP$

Junjie Luo says:

01/01/2015 at 5:36 pm

S存在性您已經證明了。但S的唯一性可以證明嗎？

- ccjou says:
  
  01/01/2015 at 10:14 pm
  
  相似變換矩陣S不具唯一性，譬如，B=SAS^{-1}=(2S)A(2S)^{-1}。
  
  - Junjie Luo says:
    
    01/03/2015 at 9:13 pm
    
    我今天也找到了一些反例，甚至不是這種倍數關係。
    
  - Junjie Luo says:
    
    01/03/2015 at 9:14 pm
    
    謝謝你的回覆。
    
Jafree says:

10/30/2016 at 4:49 am

有一个问题这几天困扰着我。向您请教一下，A的特征值、特征向量与A+A转置的特征值、特征向量的关系是怎么样的？尤其是特征向量，能数学表示出来吗？

- Jafree says:
  
  10/30/2016 at 4:50 am
  
  忘记补充一点：这里的矩阵A是行列都均一话的，即每一行的和为0，每一列的和也为0。多谢。
  
  - Jafree says:
    
    10/30/2016 at 4:51 am
    
    打错了，每一行的和为1，每一列的和也为1。。。。。
    
  - ccjou says:
    
    10/31/2016 at 8:55 am
    
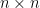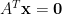    若 $n\times n$ 階矩陣 $A$ 的每一行和與列和都等於0，則 $A$ 與 $A^T$ 都有一個特徵值 0，對應特徵向量 $\mathbf{x}=(1,1,\ldots,1)$ ，即 $A\mathbf{x}=\mathbf{0}$ 且 $A^T\mathbf{x}=\mathbf{0}$ 。譬如，Laplace 矩陣，見
    https://ccjou.wordpress.com/2014/12/04/%E7%B7%9A%E6%80%A7%E4%BB%A3%E6%95%B8%E5%9C%A8%E5%9C%96%E8%AB%96%E7%9A%84%E6%87%89%E7%94%A8-%E4%B8%89%EF%BC%9A%E6%8B%89%E6%99%AE%E6%8B%89%E6%96%AF%E7%9F%A9%E9%99%A3/
    
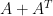    因此， $(A+A^T)\mathbf{x}=A\mathbf{x}+A^T\mathbf{x}=\mathbf{0}$ ， $A+A^T$ 也有一個特徵值 0，對應特徵向量 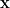$\mathbf{x}$ 。從已知的條件，我只能推得以上訊息。
    
陳威璉 says:

11/26/2016 at 10:34 pm

請問該如何證明矩陣A與其轉置矩陣具有同樣的特性根與特性向量?

- ccjou says:
  
  11/27/2016 at 9:06 am
  
  本文第一段末已證明 $A$ 與 $A^T$ 有相同的特徵多項式，因此有相同的特徵值。但特徵向量未必相同，隨便舉些例子計算即知。
  
shrine hand says:

12/20/2020 at 3:19 pm

老師好那請問一下 ATA 會與 AAT相似嗎
畢竟特徵根相同但又無法從At 相似於A這個定理推出

	Alexander Lin on 矩陣的四個基本子空間基底算法
	snowmanfat (@snowman… on 基底變換
	snowmanfat (@snowman… on 基底變換
	王偉 on Givens 旋轉於 QR 分解的應用
	猜猜看、 on 分塊矩陣的行列式
	牟家宏 on Gram-Schmidt 正交化與 QR 分解