本文的閱讀等級:初級
一個矩陣的行列式就是一個平行多面體的 (定向) 體積,這個多面體的邊對應矩陣的行。如果學生們得知了這個秘密 (在純粹代數式的教學中,這個秘密被小心地隱藏起來),那麼行列式的整個理論將成為多重線性形式理論的一部分。倘若用別的方式來定義行列式,任何敏感的人都將會永遠痛恨諸如行列式,Jacobian式,以及隱函數定理這些東西。───俄國數學家阿諾爾德 (Vladimir Arnold)〈論數學教育〉[1]
在線性代數發展歷史中,行列式和矩陣理論一直有著密切的關係。行列式概念最早出現於解線性方程組的過程中,十七世紀末,日本數學家關孝和與德國數學家萊布尼茨 (Gottfried Wilhelm Leibniz) 的著作就已使用行列式來確定線性方程組解的數目與形式[2]。十九世紀以後,矩陣的引入使得更多的行列式性質被發現,行列式的發展遂漸趨完善。今天多數線性代數教科書都會開闢一個專門討論行列式的章節,但主要的目的並非求解線性方程組,而是為了順利導入矩陣的特徵多項式。不過,美國數學教授阿斯勒 (Sheldon Axler) 卻抱持反對的態度,他認為行列式是線性代數核心原理的推導結果,而不是行列式推導出線性代數的核心原理。1994年,阿斯勒發表〈斷絕行列式〉 (Done with determinants!),該文嚴厲抨擊行列式目前於線性代數的「地位」,之後並獲得不少數學家的共鳴和迴響。阿斯勒反對行列式的理由在於行列式難以理解,不具直覺,而且常在缺乏明顯動機的情況下被引用。不僅如此,行列式與線性代數理論的基調不甚相合。行列式的計算公式與主要的矩陣運算無關,它像是從一堆矩陣元拼貼出來的蒙太奇,讓人困惑如此怪異的公式究竟是怎麼冒出來的。雖然我們無法改變或簡化行列式公式,但仍可嘗試編排出易於理解的推導過程。本文從計算平行四邊形的面積推導行列式的運算公式,這麼做雖有違行列式誕生的初衷,但此法能夠豐富行列式的幾何直覺解釋並顯現行列式的一些重要性質。
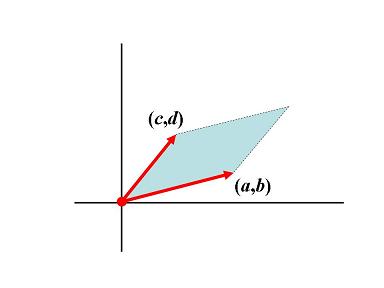
設 和
為平面上的兩個向量 (見圖一)。考慮矩陣
,我們定義函數
為
和
所張的平行四邊形面積。通常我們會揀選最便捷的解題途徑[3],不過在此我採用一種比較不尋常的作法:先找出此函數必須滿足的條件,等待條件充足後,再著手推導面積函數
的公式。
首先考慮最簡單情況:,
。兩個垂直的標準單位向量張開單位正方形,於是有下面的性質。
性質一:,其中
是單位矩陣。
再看另一個極端情況:,兩向量完全重合表示所張的平行四邊形面積等於零。
性質二:若 有相同的兩列 (row)[4],則
。
上述兩個性質仍不足以規範函數 ,我們需要更多有關平行四邊形的幾何性質,特別是所夾向量改變時,平行四邊形面積如何隨之變化。圖二顯示向量
的長度伸縮
倍,對應的平行四邊形面積亦等比例改變,因此
滿足下列關係:
。
從基礎幾何學可知 和
所張的平行四邊形面積恰為
和
所張的平行四邊形面積與
和
所張的平行四邊形面積之和 (見圖三),亦即
。
運用對稱原理,同樣也有
我們將上述線性關係合併為一個性質。
性質三:考慮 的任一列,當其他列都固定時,
為該列的線性函數。
這裡要特別強調 並非矩陣
的線性函數,也就是說,
和
不成立。對於
階矩陣
,性質三說明
推廣至 階矩陣
,則有
。
如果將 的兩列對調,
是否改變?交互使用性質二和性質三可以推出下面的結果:
性質四是性質二和性質三的必然結果。
性質四:交換 的兩列改變
的正負號。
性質四迫使函數 必須是有號 (signed) 或定向 (oriented) 面積。根據性質一,將右手拇指外的四根手指向手掌彎曲的方向視為由第一列至第二列的旋轉方向,則面積為正,反之,面積為負,此即右手定則。如果最初設定性質一為
,則按左手定則計算有號面積。另外,假如我們要求平行四邊形的面積必須為非負數,
,則性質三不復成立。我們寧可打破舊有的幾何概念接受有號面積,也不願放棄這個美好的性質:行列式是每一列的線性函數 (當固定其他列時)。
準備就緒,現在可以利用上述性質推導 函數。類似性質四的推演過程,先運用性質三來分解
,如下:
由性質二可知 ,
,再由性質四和性質一,
合併以上結果,我們導出 的計算公式:
。
這就是大家熟知的二階行列式公式。為方便辨識,我們改以 或
替代
:
。
推導行列式公式的過程雖然使用了性質四,但性質四也是由前面三個性質所導出,所以性質一、二與三唯一決定行列式的計算公式。沿用上述方法,通過推導空間中平行六面體的體積可得三階行列式公式 (見“內積與外積是怎麼來的?”)。稍後我們將以歸納法推演高階行列式的計算公式。
接著推演行列式的其他性質。不論前述的四個性質或下面介紹的性質,對任何 階方陣
都是成立的。
性質五:若 包含一個零列,則
。
以二階行列式為例,利用性質三,將純量 提出,就有
。
性質六:列取代運算,即任一列乘以常數 再加進另一列,不改變行列式。
以二階行列式為例,若第 列乘以
加進第
列,使用性質三和性質二,計算如下:
性質七:若 為三角矩陣,
等於主對角元乘積。
假設三角矩陣 的主對角元皆不含零,以列取代運算將
化簡為對角矩陣,
。
性質六指出列取代運算不改變行列式,因此 。利用性質三,逐次將
的主對角元提出,再使用性質一,可得
。
性質八:若 是一個可逆矩陣,則
;若
是不可逆的,則
。
對矩陣 執行基本列運算,將
化簡為上三角矩陣
,性質四指出列交換運算改變行列式正負號,性質六則說明列取代運算不改變行列式,因此
。再由性質七,
,推論當
是可逆時,所有
全不為零,故
;當
不可逆時,
必有一個零列,即至少有一
,則
。
性質九:
這可能是最困難證明的一個性質,下面分開兩個情況討論。若 不可逆,則
或
至少有一個是不可逆矩陣,性質八給出
。若
和
都是可逆矩陣,定義函數
。
函數 滿足上述性質一、二和三,因此
。證明如下:設
,
。
確定 滿足性質一。若
有相同兩列,則
也有相同兩列,所以
,也就有
,
滿足性質二。因為
的第
列等於
的第
列乘以
,對於
的任一列的線性組合,
的該列也有同形式的線性組合,故
和
同為該列的線性函數,因此滿足性質三。(其他證明方式請見“利用分塊矩陣證明 det(AB)=(detA)(detB)”,“矩陣乘積行列式公式的代數證法”。)
性質十:
如同性質九的證明,下面也分開兩個情況討論。若 不可逆,則
也不可逆,由性質八得知
。若
是可逆的,考慮
的 LU 分解 (見“LU 分解”),
,其中
是排列 (permutation) 矩陣 (見“特殊矩陣 (16):排列矩陣”),
和
分別為下三角和上三角矩陣,且
的主對角元全都是
。利用性質九,
。
對 取轉置,得到
,同樣根據性質九,
。
注意,三角矩陣 和
的轉置仍為三角矩陣。由性質七,得知
,且
。排列矩陣
為正交矩陣,滿足
,因此
。另外,
係由單位矩陣
持續交換列而得,可知
,故
與
必同為
或
。綜合以上結果即證得
。
另一個證法採用基本矩陣 (elementary matrix) 分解。任一可逆矩陣 可分解為
,其中
,
,是基本矩陣。引用此性質:基本矩陣的轉置不改變行列式值,即
(見“特殊矩陣 (10):基本矩陣”)。因為
,使用性質九,
我們繼續推導高階行列式的運算方法及一般公式。性質七暗示一個行列式計算方法。對方陣 執行基本列運算,僅使用列交換和列取代運算可將
化簡為上三角矩陣,因為列取代運算不改變行列式 (性質六),而列交換改變行列式的正負號 (性質四),根據性質七,即有下面的公式。
公式一:軸公式
設 為
階方陣,
為基本列運算 (僅使用列交換和列取代) 化簡
後得到的上三角矩陣,
代表所執行的列交換次數,
,
其中 的非零主對角元
即為軸元 (pivot)。
重複我們推導二階行列式的步驟可得三階行列式,總計分解為 個行列式之和,但其中僅有
個非零行列式,如下:
每個組合行列式對應一個排列矩陣 ,
代表元
出現於元位置
,
,
,排列方式計有
種:
。
對單位矩陣 執行一序列的列交換即可得到排列矩陣
,故
,
表示從
至
所執行的置換總數。所以,三階行列式公式為
下面是一般 階行列式公式。
公式二:排列公式 (或稱萊布尼茲公式)
,
其中 表示
的排列。
上述三階行列式的任一列皆可作為因數提出,繼續代入二階公式,可得到一個僅含 個行列式的表達形式,以第
列為例:
上式中,我們稱 為餘因子 (cofactor),定義如下:
,
其中 為移除
的第
列與第
行後得到的
階子陣,
稱為餘子式 (minor)。這個運算公式稱為餘因子展開或 Laplace 展開公式。
公式三:餘因子公式 (或稱 Laplace 公式)
設 為任一列指標,
。
行列式的性質同時適用於列與行 (column)。如果將 定義為行向量
和
所張的平行四邊形面積,只需要將以上討論的「列」改成「行」,並適當修改推導算式即可。另外,除了上述三個常見於教科書的行列式運算公式,還有兩個鮮為人知的運算法,有興趣進一步暸解的讀者請參閱“Chiò演算法──另類行列式計算法 ”和“Dodgson 縮合法──奇特的行列式運算法 ”。
註解
[1] On teaching mathematics,英譯文:“The determinant of a matrix is an (oriented) volume of the parallelepiped whose edges are its columns. If the students are told this secret (which is carefully hidden in the purified algebraic education), then the whole theory of determinants becomes a clear chapter of the theory of poly-linear forms. If determinants are defined otherwise, then any sensible person will forever hate all the determinants, Jacobians and the implicit function theorem.”
[2] 維基百科:行列式
[3] 設向量 且
,則
與
所張的平行四邊形的有號面積等於
(即底乘高),其中
是
與
的夾角,
。這裡要特別說明夾角
的正負號由
與
的相對位置決定。通用慣例採用右手座標系,也就是說,如果夾角
為
至
的逆時針旋轉,則
,否則
。考慮
逆時針旋轉
,設為
,則
與
的之間夾角等於
。平行四邊形的有號面積可用內積計算,如下:
。
[4] 在台灣,橫向稱為列,縱向稱為行。在中國大陸,橫向稱為行,縱向稱為列。



性質八後半句似乎有筆誤喔
謝謝你指出錯誤,已訂正。
請問
性質六適用3*3以上的行列式嗎?
因為我對5*5作列運算,結果行列式的值變了…
以上所有性質對任意nxn階矩陣皆成立,請檢查確認計算過程無誤。
大師好
有個矩陣假如2by3
1-2j 1+3j 2+j
2-3j 1-2j 2-5j
想要把1-2j 那項變1
是可以把矩陣全部項都除以1-2j嗎?
還是要怎麼做
1 0
2 3
2 4
和
1 0
2 3
1 2
兩個矩陣有一樣嗎
2 4可以直接化簡成1 2嗎
恕我無法回答,但你可以自創一套矩陣代數,放入自己喜歡的定義與公理。
他意思就是说你菜逼
不过这个人确实牛批👍🏻
是我想法有錯嗎?
建議你在提問前:
1) 先做好必要的功課;
2) 想清楚問題是甚麼再問。
否則別人會視你為民科或大濕:
https://zh.wikipedia.org/wiki/%E6%B0%91%E9%97%B4%E7%A7%91%E5%AD%A6%E5%AE%B6
你好
假如我在計算高階的行列式值比如說 4X4 5X5 甚至更多
假如不用降階的方法去計算
還有其他方法嗎
我記得3X3 可以在旁邊在加上原本矩陣的兩行去計算
不知道更高階是否也有這種規律或規則
謝謝
我所知道的方法即如上文所述以及文末的連結。
老師您好

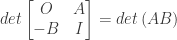
 ,
, 是一個m*m的單位矩陣。計算
是一個m*m的單位矩陣。計算

 , where A, B are matrices of dimension p*q and q*p, respectively.
, where A, B are matrices of dimension p*q and q*p, respectively.
我是資工系的學生
最近看到了幾個與行列式相關的題目,想請老師指點破題方向
或是提供資料我去閱讀
1.有四個n*n 的矩陣 A, B, C, D,且A矩陣可逆,要證明
接者我有看到其他類似的題目,想一起問老師如何用他真實的函義看待這種題目
2.若 A 是一個 m*n 的矩陣、B是一個 n*m 的矩陣,推出
3.令
4.Show that
5.Show that
老師我真的不懂的是為甚麼矩陣拚湊起來可以有這樣的性質,那這樣的性質代表了矩陣或向量有什麼關係。