LU 分解

本文的閱讀等級：初級

令 $A$ 為一個 $n\times n$ 階矩陣。LU 分解是指將 $A$ 表示為兩個 $n\times n$ 階三角矩陣的乘積

$A=LU$ ，

其中 $L$ 是下三角矩陣， $U$ 是上三角矩陣。見下例，

$\left[\!\!\begin{array}{rrc} 3&-1&2\\ 6&-1&5\\ -9&7&3 \end{array}\!\!\right]=\left[\!\!\begin{array}{rcc} 1&0&0\\ 2&1&0\\ -3&4&1 \end{array}\!\!\right]\left[\!\!\begin{array}{crc} 3&-1&2\\ 0&1&1\\ 0&0&5 \end{array}\!\!\right]$ 。

LU 分解的本質是高斯消去法的一種表達形式，矩陣 $L$ 記錄消去法化簡 $A$ 的過程，矩陣 $U$ 則儲存化簡結果 (見“高斯消去法”)。LU 分解的外表看似平淡無奇，但它可以用來解線性方程，逆矩陣與計算行列式，堪稱是最具實用價值的矩陣分解式之一。

高斯消去法

我用一個例子說明如何從高斯消去法推演 LU 分解。考慮底下的線性方程 $A\mathbf{x}=\mathbf{b}$ 求解問題：

$\left[\!\!\begin{array}{rrc} 3&-1&2\\ 6&-1&5\\ -9&7&3 \end{array}\!\!\right]\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}=\left[\!\!\begin{array}{r} 10\\ 22\\ -7 \end{array}\!\!\right]$ 。

高斯消去法應用於求解線性方程的基本想法十分簡單。在保證不破壞解集合的前提下，運用下述基本列運算 (elementary row operation) 將增廣矩陣 $\begin{bmatrix} A\vert\mathbf{b} \end{bmatrix}$ 化簡至三角矩陣 (在台灣，橫向稱為列，縱向稱為行。在中國大陸，橫向稱為行，縱向稱為列。)：

交換：將列 $i$ 與列 $j$ 對調，以符號表示為

$\mathrm{row}_i\leftrightarrow\mathrm{row}_j$ ；
伸縮：列 $i$ 通乘非零常數 $c$ ，

$\mathrm{row}_i\leftarrow c\times\mathrm{row}_i$ ；
取代：將列 $j$ 通乘非零常數 $l_{ij}$ 的結果加進列 $i$ ，

$\mathrm{row}_i\leftarrow\mathrm{row}_i-l_{ij}\times\mathrm{row}_j$ 。

取代是主要的化簡工具。列取代運算的目的在消去矩陣的 $(i,j)$ 元，因此乘數 $l_{ij}$ 必須滿足 $a_{ij}-l_{ij}a_{jj}=0$ ，如下所示：

$\begin{bmatrix} \ast&\cdots&\ast&\ast&\ast&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&\cdots&0&a_{jj}&\ast&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&\cdots&0&a_{ij}&\ast&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \end{bmatrix}\rightarrow\begin{bmatrix} \ast&\cdots&\ast&\ast&\ast&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&\cdots&0&a_{jj}&\ast&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&\cdots&0&a_{ij}-l_{ij}a_{jj}&\ast&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots \end{bmatrix}$ 。

若 $a_{jj}\neq 0$ ，我們稱 $a_{jj}$ 為軸元 (pivot)，乘數等於被消去元除以軸元， $l_{ij}=a_{ij}/a_{jj}$ 。下面僅寫出係數矩陣 $A$ 的消去過程：

$\left[\!\!\begin{array}{rrc} 3&-1&2\\ 6&-1&5\\ -9&7&3 \end{array}\!\!\right]\xrightarrow[]{l_{21}=2}\left[\!\!\begin{array}{rrc} 3&-1&2\\ 0&1&1\\ -9&7&3 \end{array}\!\!\right]\xrightarrow[]{l_{31}=-3}\left[\!\!\begin{array}{rrc} 3&-1&2\\ 0&1&1\\ 0&4&9 \end{array}\!\!\right]\xrightarrow[]{l_{32}=4}\left[\!\!\begin{array}{crc} 3&-1&2\\ 0&1&1\\ 0&0&5 \end{array}\!\!\right]$ 。

令 $U$ 為列運算最後得到的上三角矩陣， $U$ 的主對角元 $3$ ， $1$ ， $5$ 即為消去過程所使用的軸元。如果一個 $n$ 階方陣有完整的 $n$ 個軸元，亦即 $U$ 的主對角元皆不為零，則 $A$ 稱為非奇異 (nonsingular) 矩陣，即可逆 (invertible) 矩陣 (因為線性方程 $A\mathbf{x}=\mathbf{b}$ 恆有解)。

LU 分解

高斯消去法可以通過一連串的矩陣乘法來實現。每一個基本列運算等同於左乘一個基本矩陣 (見“特殊矩陣(10)：基本矩陣”)，而對應列取代的基本矩陣 $E_{ij}$ 的 $(i,j)$ 元即為 $-l_{ij}$ 。上例中，基本矩陣依序是

$E_{21}=\left[\!\!\begin{array}{rcc} 1&0&0\\ -2&1&0\\ 0&0&1 \end{array}\!\!\right],~E_{31}=\begin{bmatrix} 1&0&0\\ 0&1&0\\ 3&0&1 \end{bmatrix},~E_{32}=\left[\!\!\begin{array}{crc} 1&0&0\\ 0&1&0\\ 0&-4&1 \end{array}\!\!\right]$ 。

消去程序可用下列矩陣乘法表示：

$E_{32}E_{31}E_{21}A=U$ 。

基本矩陣 $E_{ij}$ 都是可逆的，且其逆矩陣也是基本矩陣，寫出

$A=E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}U=LU$ ，

其中 $L$ 是下三角矩陣，計算得到

$\begin{aligned} L&=E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}\\ &=\begin{bmatrix} 1&0&0\\ 2&1&0\\ 0&0&1 \end{bmatrix}\left[\!\!\begin{array}{rcc} 1&0&0\\ 0&1&0\\ -3&0&1 \end{array}\!\!\right]\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&4&1 \end{bmatrix}=\left[\!\!\begin{array}{rcc} 1&0&0\\ 2&1&0\\ -3&4&1 \end{array}\!\!\right].\end{aligned}$

仔細觀察 $L$ 矩陣可發現一個奇特的現象： $L$ 的主對角線下的三個元剛好等於列取代運算的乘數 $l_{ij}$ ， $i>j$ 。這不是巧合，而是必然成立。為了保有這個優美的性質，我們決定對 $L$ 矩陣加入一項新的限制： $L$ 的主對角元必須都是 $1$ ，稱為單位下三角矩陣 (unitriangular matrix)。利用基本矩陣性質，不難證明單位下三角矩陣的逆矩陣也是一個單位下三角矩陣，同理，單位上三角矩陣的逆矩陣也是一個單位上三角矩陣。

前例 LU 分解的主要結果整理於下。若 $A$ 是一個 $n\times n$ 階可逆矩陣且 $A=LU$ ，則單位下三角矩陣 $L$ 和上三角矩陣 $U$ 具有以下性質：

對於 $i=1,\ldots,n$ ， $l_{ii}=1$ 且 $u_{ii}\neq 0$ 。
$U$ 是對 $A$ 執行高斯消去法所得到的結果。
$L$ 的主對角線下各元 $l_{ij}$ ， $i>j$ ，記錄所執行的列取代運算的乘數。

下面證明性質 (3)。為方便說明，考慮三階矩陣的 LU 分解：

$LU=\begin{bmatrix} 1&0&0\\ l_{21}&1&0\\ l_{31}&l_{32}&1 \end{bmatrix}\begin{bmatrix} \mathrm{row}_1(U)\\ \mathrm{row}_2(U)\\ \mathrm{row}_3(U) \end{bmatrix}=\begin{bmatrix} \mathrm{row}_1(A)\\ \mathrm{row}_2(A)\\ \mathrm{row}_3(A) \end{bmatrix}=A$ 。

欲消去 $L$ 主對角線下方的三個元，同時對等號兩側執行列運算，依序是

$\begin{aligned} \mathrm{row}_2&\leftarrow\mathrm{row}_2-l_{21}\times\mathrm{row}_1\\ \mathrm{row}_3&\leftarrow\mathrm{row}_3-l_{31}\times\mathrm{row}_1\\ \mathrm{row}_3&\leftarrow\mathrm{row}_3-l_{32}\times\mathrm{row}_2.\end{aligned}$

如此便將 $L$ 化簡為單位矩陣 $I$ ，等號左邊於是等於 $IU$ 。又對等號右邊的 $A$ 矩陣進行同樣的列運算，這其實就是消去法的運算步驟，結果當然等於上三角矩陣 $U$ ，證得等號左邊 $LU$ 與右邊 $A$ 相等。

存在性

然而，並非任何可逆矩陣都具有 LU 分解形式，例如， $A=\begin{bmatrix} 0&2\\ 1&3 \end{bmatrix}$ 。假若 $A$ 可以寫為

$A=LU=\begin{bmatrix} 1&0\\ l_{21}&1 \end{bmatrix}\begin{bmatrix} u_{11}&u_{12}\\ 0&u_{22} \end{bmatrix}$ ，

則必有 $u_{11}=0$ ， $U$ 是不可逆的，這與 $LU=A$ 為可逆矩陣的事實相互矛盾。矩陣 $A$ 之所以不存在 $LU$ 分解的原因在於 $0$ 占據了 $(1,1)$ 元，但軸元必須不為零才能產生乘數。根據這項觀察，即知可逆矩陣 $A$ 的 LU 分解存在條件是：列運算過程中， $0$ 不得在軸元位置。萬一碰上零軸元的情況，還是有補救辦法，那就是使用列交換運算設法產生其他非零軸元，不過 LU 分解要修改成 $PA=LU$ ， $P$ 是排列矩陣。例如，

$\begin{aligned} PA&=\begin{bmatrix} 0&1\\ 1&0 \end{bmatrix}\begin{bmatrix} 0&2\\ 1&3 \end{bmatrix}=\begin{bmatrix} 1&3\\ 0&2 \end{bmatrix}\\ &=\begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}\begin{bmatrix} 1&3\\ 0&2 \end{bmatrix}=LU.\end{aligned}$

關於 $PA=LU$ 演算法介紹，請見“PA=LU 分解”。

在不執行消去法的前提下，底下介紹一個判斷可逆矩陣 $A$ 是否存在 LU 分解的方法。考慮命題：若 $n\times n$ 階可逆矩陣 $A$ 有 LU 分解，則 $A$ 的所有 $k\times k$ 階領先主子陣 (leading principal submatrix) $A_k$ 都是可逆的。將 LU 分解以分塊矩陣表示為

$A=LU=\begin{bmatrix} L_{11}&0\\ L_{21}&L_{22} \end{bmatrix}\begin{bmatrix} U_{11}&U_{12}\\ 0&U_{22} \end{bmatrix}=\begin{bmatrix} L_{11}U_{11}&L_{11}U_{12}\\ L_{21}U_{11}&L_{21}U_{12}+L_{22}U_{22} \end{bmatrix}$ ，

其中 $L_{11}$ 和 $U_{11}$ 是 $k\times k$ 階分塊。因為 $L_{11}$ 和 $U_{11}$ 同為三角矩陣且包含非零主對角元，兩者皆是可逆的，故 $A_k=L_{11}U_{11}$ 也是可逆的。上例中，方陣 $A$ 的領先主子陣

$A_1=\begin{bmatrix} 3 \end{bmatrix}=\begin{bmatrix} 1 \end{bmatrix}\begin{bmatrix} 3 \end{bmatrix},~~A_2=\begin{bmatrix} 3&-1\\ 6&-1 \end{bmatrix}=\begin{bmatrix} 1&0\\ 2&1 \end{bmatrix}\left[\!\!\begin{array}{cr} 3&-1\\ 0&1 \end{array}\!\!\right]$ ，

和 $A_3=A=LU$ 全都是可逆的。此性質的反向陳述可用來判定 $A$ 是否有 LU 分解：若 $A$ 的所有領先主子陣 $A_k$ 都是可逆的，則存在 LU 分解。證明採用歸納法。若 $k=1$ ，明顯地，若 $A_1=[a_{11}]$ 是可逆的， $a_{11}\neq 0$ ， $A_1=[1][a_{11}]$ 即為 LU 分解式。假設 $k\times k$ 階領先主子陣 $A_k$ 是可逆的並有 LU 分解 $A_k=L_kU_k$ ，將 $(k+1)\times(k+1)$ 階領先主子陣 $A_{k+1}$ 表示為 $A_{k+1}=\begin{bmatrix} A_k&\mathbf{b}\\ \mathbf{c}^T&d \end{bmatrix}$ ，其中 $\mathbf{b}$ 和 $\mathbf{c}$ 是 $k$ 維向量， $d$ 是純量。寫出

$A_{k+1}=\begin{bmatrix} A_k&\mathbf{b}\\ \mathbf{c}^T&d \end{bmatrix}=\begin{bmatrix} L_k&\mathbf{0}\\ \mathbf{x}^T&1 \end{bmatrix}\begin{bmatrix} U_k&\mathbf{y}\\ \mathbf{0}^T&z \end{bmatrix}$ ，

乘開右項，比較等號兩邊可得

$\mathbf{b}=L_k\mathbf{y},~~\mathbf{c}^T=\mathbf{x}^TU_k,~~d=\mathbf{x}^T\mathbf{y}+z$ 。

上式可解出 $\mathbf{y}=L_k^{-1}\mathbf{b}$ ， $\mathbf{x}^T=\mathbf{c}^TU_k^{-1}$ ， $z=d-\mathbf{x}^T\mathbf{y}=d-\mathbf{c}^TU_k^{-1}L_k^{-1}\mathbf{b}=d-\mathbf{c}^TA_k^{-1}\mathbf{b}$ ，就有 $A_{k+1}=L_{k+1}U_{k+1}$ ，其中

$L_{k+1}=\begin{bmatrix} L_k&\mathbf{0}\\ \mathbf{c}^TU_{k}^{-1}&1 \end{bmatrix},~U_{k+1}=\begin{bmatrix} U_k&L_k^{-1}\mathbf{b}\\ \mathbf{0}^T&d-\mathbf{c}^TA_{k}^{-1}\mathbf{b} \end{bmatrix}$ 。

因為 $A_{k+1}$ 與 $L_{k+1}$ 是可逆的，故知 $U_{k+1}=A^{-1}_{k+1}L_{k+1}$ 也是可逆的，推論 $d-\mathbf{c}^TA_k^{-1}\mathbf{b}\neq 0$ 。歸納得知 $A=A_n$ 有 LU 分解 $A=L_nU_n$ 。

唯一性

如果某甲和某乙各自算出滿足上述三個性質的 LU 分解，他們兩人會得到相同的 LU 分解嗎？也就是說，矩陣 $A$ 的 LU 分解是唯一的嗎？探索這個問題需要運用一些矩陣代數技巧。我們曉得 LU 分解的 $L$ 主對角元皆為 $1$ ，而 $U$ 則否，兩者呈現「非對稱性」。因為 $u_{ii}$ 不等於零， $U$ 可進一步分解為

$\begin{bmatrix} u_{11}&u_{12}&u_{13}\\ 0&u_{22}&u_{23}\\ 0&0&u_{33} \end{bmatrix}=\begin{bmatrix} u_{11}&0&0\\ 0&u_{22}&0\\ 0&0&u_{33} \end{bmatrix}\begin{bmatrix} 1&u_{12}/u_{11}&u_{13}/u_{11}\\ 0&1&u_{23}/u_{22}\\ 0&0&1 \end{bmatrix}$ 。

令 $D=\mathrm{diag}(u_{11},u_{22},u_{33})$ ，並重新定義上式最右側矩陣為 $U$ ，如此一來， $L$ 和 $U$ 的主對角元皆為 $1$ (即單位三角矩陣)， $A$ 也就可以表示為 $A=LDU$ ，稱作 LDU 分解，如下例，

$\begin{aligned} A&=\left[\!\!\begin{array}{rrc} 3&-1&2\\ 6&-1&5\\ -9&7&3 \end{array}\!\!\right]\\ &=\left[\!\!\begin{array}{rcc} 1&0&0\\ 2&1&0\\ -3&4&1 \end{array}\!\!\right]\begin{bmatrix} 3&0&0\\ 0&1&0\\ 0&0&5 \end{bmatrix}\left[\!\!\begin{array}{crr} 1&-1/3&2/3\\ 0&1&1\\ 0&0&1 \end{array}\!\!\right]\\ &=LDU.\end{aligned}$

利用 LDU 分解很容易證明 LU 分解的唯一性。假設 $A=L_1D_1U_1$ ， $A=L_2D_2U_2$ ，你只要證明 $L_1=L_2$ ， $D_1=D_2$ ， $U_1=U_2$ 即可。考慮關係式

$L_1D_1U_1=L_2D_2U_2$ 。

已知 $L_i$ 和 $U_i$ 都是可逆的，上式左乘 $L_1^{-1}$ ，右乘 $U_2^{-1}$ ，可得

$D_1U_1U_2^{-1}=L_1^{-1}L_2D_2$ 。

以三階矩陣為例，乘開得到下列矩陣型態：

$\begin{bmatrix} (D_1)_{11}&\ast&\ast\\ 0&(D_1)_{22}&\ast\\ 0&0&(D_1)_{33} \end{bmatrix}=\begin{bmatrix} (D_2)_{11}&0&0\\ \ast&(D_2)_{22}&0\\ \ast&\ast&(D_2)_{33} \end{bmatrix}$ 。

比較等號兩側的主對角元得知 $D_1=D_2$ ，再比較非主對角元，確認 $\ast=0$ ，因此斷定 $U_1U_2^{-1}=I$ ， $L_1^{-1}L_2=I$ ，證得 $U_1=U_2$ 且 $L_1=L_2$ 。

應用

最後討論 LU 分解的應用。LU 分解不僅僅只是記錄消去過程，它還有一個非常重要的實際用途：LU 分解具備快速求解線性方程 $A\mathbf{x}=\mathbf{b}$ 的良好結構。一旦得到了可逆矩陣 $A$ 的 LU 分解 $A=LU$ ，我們大可把 $A$ 拋棄，將 $A\mathbf{x}=\mathbf{b}$ 改為 $L(U\mathbf{x})=\mathbf{b}$ ，再令 $\mathbf{y}=U\mathbf{x}$ ，原線性方程等價於兩組三角形系統：

$\begin{aligned} L\mathbf{y}&=\mathbf{b}\\ U\mathbf{x}&=\mathbf{y}. \end{aligned}$

接著使用兩次迭代即可得到解。上例中，先以正向迭代解出 $\mathbf{y}$ ，

$\left[\!\!\begin{array}{rcc} 1&0&0\\ 2&1&0\\ -3&4&1 \end{array}\!\!\right]\begin{bmatrix} y_1\\ y_2\\ y_3 \end{bmatrix}=\left[\!\!\begin{array}{r} 10\\ 22\\ -7 \end{array}\!\!\right]\Rightarrow\begin{cases} y_1=10&\\ y_2=-2y_1+22=2&\\ y_3=3y_1-4y_2-7=15& \end{cases}$

再以反向迭代解出 $\mathbf{x}$ ，

$\left[\!\!\begin{array}{crc} 3&-1&2\\ 0&1&1\\ 0&0&5 \end{array}\!\!\right]\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}=\left[\!\!\begin{array}{r} 10\\ 2\\ 15 \end{array}\!\!\right]\Rightarrow\begin{cases} x_1=(x_2-2x_3+10)/3=1&\\ x_2=-x_3+2=-1&\\ x_3=15/5=3& \end{cases}$

對於 $n\times n$ 階矩陣 $A$ ，LU 分解耗費的乘法運算量大約是 $\frac{1}{3}n^3$ ^[1]，與高斯消去法相同。這個數字其實不算太糟，因為兩個 $n$ 階方陣相乘就使用了 $n^3$ 次運算。另外，正向迭代或反向迭代的運算量都只有 $\frac{1}{2}n^2$ ，遠比 LU 分解來的少。所以，如果只要解出單一線性系統 $A\mathbf{x}=\mathbf{b}$ ，直接用消去法化簡增廣矩陣 $\begin{bmatrix} A\vert\mathbf{b} \end{bmatrix}$ 和 LU 分解的兩段式解法兩者之間並沒有多大差別，但如果稍後還要解多個係數矩陣相同但常數向量改變的系統 $A\mathbf{x}=\mathbf{b}^{\prime}$ ，LU 分解便能夠派上用場。舉例來說，LU 分解可以用來計算逆矩陣 $A^{-1}$ 。將矩陣方程 $AX=A\begin{bmatrix} \mathbf{x}_1&\mathbf{x}_2&\mathbf{x}_3 \end{bmatrix}=I$ 看成三個線性方程：

$A\mathbf{x}_1=\begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix},~ A\mathbf{x}_2=\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix},~ A\mathbf{x}_3=\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}$ ，

解出的未知向量 $\mathbf{x}_1$ ， $\mathbf{x}_2$ ， $\mathbf{x}_3$ 就是逆矩陣 $A^{-1}$ 的三個行向量。

LU 分解還可以用來計算 $n\times n$ 階行列式。根據矩陣乘積的行列式可乘公式

$\det A=\det(LU)=(\det L)(\det U)$ ，

三角矩陣的行列式等於主對角元乘積，因此 $\mathrm{det}L=1$ ，推論

$\det A=\det U=\displaystyle\prod_{i=1}^nu_{ii}$ 。

方陣 $A$ 的行列式即為消去法所得到的上三角矩陣 $U$ 主對角元之積 (關於其他行列式計算方法的介紹，請見“Chiò 演算法──另類行列式計算法”)。

註解
[1] 引用來源 Gilbert Strang, Introduction to Linear Algebra, fourth edition, Wellesley Cambridge Press, pp 99, 2009.

16 Responses to LU 分解

levinc417 says:

01/31/2012 at 11:39 am

請問老師，有其他比較快判斷是否可以LU分解的方法嗎？還是只有軸元為零時不可LU分解？
因為在LU解線性方程那邊，有個有趣的事情: “A要能LU分解”! 為了判斷能不能分解，做完啦啦喳喳運算確認後再來解線性方程AX=b，那直接解線性方程不是比較快？而且有點多此一舉的感覺欸~

- ccjou says:
  
  01/31/2012 at 11:59 am
  
  答案在第一段末：
  
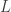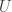  LU 分解的本質是高斯消去法的一種表達形式， $L$ 矩陣記錄消去法化簡 $A$ 矩陣的過程，而 $U$ 矩陣則儲存化簡結果。
  
  而高斯消去法的目的即在解線性方程，那些啦啦喳喳運算是免不掉的。
  
Pan Myautsai says:

04/30/2013 at 11:04 am

很精彩的解析，非常感謝！
另外好像有幾處筆誤：
比如：「交換：將列 i 和列 j 對調，以符號表示為」
應該是：
「交換：將行 i 和行 j 對調，以符號表示為」

- ccjou says:
  
  04/30/2013 at 1:24 pm
  
  謝謝。你說的筆誤是個誤會。在台灣，column稱為行，row稱為列。大陸的用法恰巧相反，見
  
  兩岸線性代數用詞參照
  
  - Pan Myautsai says:
    
    04/30/2013 at 1:26 pm
    
    原來是這樣子！又科普了，再次感謝！
    
DJ says:

04/12/2015 at 7:35 pm

我媽問我說為什麼跪著看電腦真的太神了
快速又不太會發生計算錯誤,謝謝老師~~

小马_xiaoLV5 says:

06/26/2015 at 5:22 pm

HAHA, 我看这个 “行“”列”有些不对劲，原来是大陆和台湾的习惯问题

Zuowen says:

12/19/2016 at 10:49 pm

老师您好，您的文章非常简明扼要，易读，我看了以后马上就明白了。就是有一个地方，因为我是学计算机的所以知道，很乐意和您分享，两个矩阵相乘是可以做到比n^3更低的复杂度的，比如施特拉森演算法 https://zh.wikipedia.org/wiki/%E6%96%BD%E7%89%B9%E6%8B%89%E6%A3%AE%E6%BC%94%E7%AE%97%E6%B3%95
祝您工作愉快。

- ccjou says:
  
  12/19/2016 at 11:08 pm
  
  謝謝分享。我也是學了線性代數多年以後才知這個算法，：
  
  Strassen 演算法──分治矩陣乘法
  
Hunts says:

01/17/2017 at 7:04 pm

教授您好，存在性證明的倒數第五行是否漏掉了”d-“？

- ccjou says:
  
  01/17/2017 at 7:43 pm
  
  謝謝指正。
  
  - Hunts says:
    
    01/18/2017 at 10:20 am
    
    另有一處不太能理解，存在性證明的倒數第八行，不就在還沒證明出來的情況下就假設存在LU分解了嗎？因為老師直接寫出了LU分解式。謝謝老師！
    
    - ccjou says:
      
      01/18/2017 at 10:27 am
      
      這是數學歸納法。假定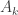 $A_k$ 有LU分解，然後證明 $A_{k+1}$ 有LU分解。
      
Tianyu says:

10/25/2017 at 11:56 pm

老师您好：

首先非常感谢您花费时间心血建立的这样一个博客，实在获益良多。

然后在读到这一章的时候，对LU分解的存在性有一点疑问：在维基百科中，其对存在性条件的表述为“实际上，如果一个秩为k的矩阵的前k个顺序主子式不为零，那么它就可以进行LU分解，但反之则不然。”

似乎这个条件并一定要求A为可逆矩阵（而在您的文章中，存在性的证明是对于“下面補充一個在不執行消去法的前提下，可逆矩陣 A 是否存在 LU 分解的判斷方法。”）。

于是想请问一下到底A是否要为可逆矩阵呢？

谢谢！

- nekomoon404 says:
  
  12/15/2019 at 4:01 pm
  
  我觉得A不需要是可逆矩阵，LU分解的条件是A若为n阶矩阵，A的1,2，…，n-1阶顺序主子式不为0。如果这样的矩阵A的n阶主子式，即行列式为0，那么它是不可逆的，但是可以LU分解。不知道这样理解对不对
  
loren Liu says:

06/08/2018 at 3:15 pm

十分感謝教授耐心細緻的講解；
也給出了一些暖心的細節；
謝謝教授

	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明
	悟 on 條件機率與貝氏定理
	jeremy on 內積與外積是怎麼來的？

LU 分解

16 Responses to LU 分解

Leave a comment Cancel reply

搜尋(繁體中文或英文)

訊息看板

近期文章

線性代數專欄

其他主題專欄

每週問題

數據充分性問題

其他分類

Recent Comments

近期最多人點閱

分類

Archives

標籤雲

線代線上影音課程

線代學習網站

線代電子書

矩陣計算器

LaTeX

Blogroll

訂閱

閱讀導引

學習資源

專題探究

急救查詢

其他分頁

Meta

網路狀態

Blog Stats

LU 分解

Share this:

16 Responses to LU 分解

Leave a comment Cancel reply

搜尋(繁體中文或英文)

訊息看板

近期文章

線性代數專欄

其他主題專欄

每週問題

數據充分性問題

其他分類

Recent Comments

近期最多人點閱

分類

Archives

標籤雲

線代線上影音課程

線代學習網站

線代電子書

矩陣計算器

LaTeX

Blogroll

訂閱