本文的閱讀等級:中級
令 是一個
階可逆矩陣。LU 分解
是高斯消去法的一種表達形式,下三角矩陣
記錄消元過程使用的乘數,上三角矩陣
儲存約化結果,其中
和
的主對角元分別滿足
和
(見“LU 分解”)。不過,並非每一可逆矩陣都存在 LU 分解。在執行高斯消去法的化簡程序中,若
出現在軸元 (pivot) 位置,即
元,列取代運算便無法消去軸元底下各元,這時標準 LU 分解不復存在。可逆矩陣
的軸元總數 (即
) 等於
,透過列交換運算必能獲得一個 (非零) 軸元,所以仍可繼續下一階段的化簡步驟。從實際面來看,縱使未發生「零軸元」的情況 (軸元所在位置為零),為了避免因不當使用消去法而引發災難,部分軸元法 (partial pivoting) 也會適時地交換列 (見“特殊矩陣 (12):對角佔優矩陣”)。見下例 (取自[1]):
。
從 同時包含數值很小和很大的主對角元可知
不具數值穩定性,也就是說,標準 LU 分解將原本是良置的 (well-conditioned)
分解出病態的 (ill-conditioned)
[2]。問題發生的根源在於軸元的數值太小,交換
的列以取得數值較大的軸元是最簡單的解決方法。所謂部分軸元法是指在每一次消元步驟進行之前,先搜尋軸元所在位置及其底下的所有元,從其中選出數值 (絕對值) 最大的元,並交換兩列將最大元置於軸元位置。回到前例,令
,
的 LU 分解可有效改善數值穩定性,結果如下:
。
我們可能認為在計算 LU 分解之前,必須先確定 的列排序,即排列矩陣
。這是錯覺,其實無此必要。但如果化簡
的過程中混合了列交換與消元運算,還能保證可逆矩陣
必可化約成
形式嗎?答案是肯定的,本文將探討這個問題,並給出一個實用的演算法。
在高斯消去法將 約化成上三角矩陣
的過程中,如欲消去
元,
,令列
減去列
通乘一乘數
,此運算可表示為消元基本矩陣
(見“特殊矩陣 (10):基本矩陣”)。如欲交換列
和列
,則使用排列基本矩陣
。例如,
。
下面我們用一個例子來說明容許列交換運算的高斯消去法。為便利說明,我們不使用部分軸元法,僅在遇見「零軸元」時才執行列交換;同時為容易辨識,在消元產生的零元下加註一底線。過程如下:
其中 是不需要執行的虛擬運算。將以上化簡過程表示成矩陣乘積:
。
想像吾人有未卜先知能力,在消元步驟前提早將 的各列排序妥當,即得
。不過如此一來,基本矩陣
勢必跟著改變,設為
,就有
。
令 ,
,上式即可表示為
。
接下來只要確定 也是消元基本矩陣,
即符合要求:
且
,
。因為
,可得
其中
這裡有兩件事必須注意。第一,上例中 ,
,皆為消元基本矩陣。一般情況也成立,理由如下:列交換運算總是在消去軸元
底下各元後啟動,令
,
,則
,可知
也是一個消元基本矩陣。第二, 所含的乘數
隨列交換運算
移動位置。若
,則
;若
,則
;若
,
,則
。
根據以上討論結果,我們可以設計一個演算法來記錄高斯消去法的執行過程與結果,包括下三角矩陣 所儲存的乘數
,
,排列矩陣
的列排序,以及上三角矩陣
,
。實際作法是引進一個增廣矩陣,在給定矩陣
的最右側加入一行代表列排序,設初始值為
,並於消元過程產生的零元位置 (即上例加註底線者) 填入所使用的乘數,同樣也加註一底線以利辨識。請特別注意:執行消元運算時,我們不計算代表列排序的最右行與儲存的乘數,但列交換運算則不受此限。完整過程如下:
從最後得到的增廣矩陣即可寫出 分解。最末行顯示列排序為
,對應排列矩陣
,
下三角矩陣 和上三角矩陣
則分別為
。
註解:
[1] Gene H. Golub and Charles F. Van Loan, Matrix Computations, 2nd edition, 1989.
[2] 條件數 (condition number) 是一個判斷矩陣是否為良置或病態的標準方法 (詳見“條件數)。對於一個 階可逆矩陣
,令
為最大奇異值,
為最小奇異值。矩陣
的條件數定義為
。若
接近
,則
是良置系統;若
很大,則
是病態系統。上例中,
的條件數為
,可知
是良置的;
的條件數為
,可知
是病態的。

請問周老師:
為什麼
等於
, 而
的意思嗎?
比較易懂,有橫式表達法嗎?
看到
同理
如果沒有特別指明,線性代數社群習慣使用行向量 (column),故

此運算稱為outer product,但稱「外積」容易與cross product混淆。維基百科介紹:
http://en.wikipedia.org/wiki/Outer_product
謝謝 ,原來是外積, 。之前一直以為是內積。
。之前一直以為是內積。
參考,“特殊矩陣 (10):基本矩陣” ,所以 排列矩陣是
排列矩陣是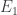 型。
型。
基本矩陣
有幫助!謝謝!!!
教授您好,請教您,若是不藉由擴充矩陣的演算法,而是依循您演算法之前的說明來拆解基本矩陣乘積,卻無法求出正確分解,不知何處犯錯呢? 如下:
按照上述變換過程後,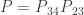 ,
,

似乎應該
但代入驗算後卻明顯有誤???
懇請教授賜教,謝謝
你最後得到的
謝謝教授指導,我明白哪邊有誤了
Thanks a lot for your explanation. It helps a lot!
However, I am still wondering the solution of Permutation matrix.
Especially the algorithm for calculating P. Looking forward to your reply.
Apropo, I’m from mainland. Therefore, I am really grateful if your answer is in traditional Chinese.
Cuz I could only read them rather than type and write.
Thanks!