特殊矩陣 (14)：Gramian 矩陣

本文的閱讀等級：中級

設 $A$ 為一個 $m\times n$ 階實矩陣， $n$ 階方陣 $G=[g_{ij}]=A^TA$ 稱為 Gramian 或 Gram 矩陣，也有人稱之為交互乘積 (cross-product) 矩陣。考慮 $A$ 的行向量表達式 $A=\begin{bmatrix} \mathbf{a}_1&\mathbf{a}_2&\cdots&\mathbf{a}_n \end{bmatrix}$ ， $\mathbf{a}_i\in\mathbb{R}^m$ ，則

$G=A^TA=\begin{bmatrix} \mathbf{a}_1^T\\ \mathbf{a}_2^T\\ \vdots\\ \mathbf{a}_n^T \end{bmatrix}\begin{bmatrix} \mathbf{a}_1&\mathbf{a}_2&\cdots&\mathbf{a}_n \end{bmatrix}=\begin{bmatrix} \mathbf{a}_1^T\mathbf{a}_1&\mathbf{a}_1^T\mathbf{a}_2&\cdots&\mathbf{a}_1^T\mathbf{a}_n\\ \mathbf{a}_2^T\mathbf{a}_1&\mathbf{a}_2^T\mathbf{a}_2&\cdots&\mathbf{a}_2^T\mathbf{a}_n\\ ~&~&~&~\\ \mathbf{a}_n^T\mathbf{a}_1&\mathbf{a}_n^T\mathbf{a}_2&\cdots&\mathbf{a}_n^T\mathbf{a}_n \end{bmatrix}$ ，

這指出 $g_{ij}=\mathbf{a}_i^T\mathbf{a}_j$ 。推廣至一般情況，設向量集 $\mathbf{v}_1,\mathbf{v}_2,\ldots,\mathbf{v}_n$ 屬於內積空間 $\mathcal{V}$ ， $n\times n$ 階 Gramian 矩陣 $G$ 的 $(i,j)$ 元定義為 $\mathbf{v}_i$ 和 $\mathbf{v}_j$ 的內積，以 $g_{ij}=\left\langle\mathbf{v}_i,\mathbf{v}_j\right\rangle$ 表示 (見“內積的定義”)。

Jørgen Pedersen Gram (1850-1916) From http://upload.wikimedia.org/wikipedia/commons/a/ab/Jorgen_Gram.jpg

本文僅討論廣泛應用於統計學與控制系統的實 Gramian 矩陣，以下列舉幾個實 Gramian 矩陣 $G=A^TA$ 的基本性質。

(1) $A^TA$ 是對稱矩陣。

明顯地， $g_{ij}=\mathbf{a}_i^T\mathbf{a}_j=\mathbf{a}_j^T\mathbf{a}_i=g_{ji}$ 。

(2) 對任一實矩陣 $A$ ， $\mathrm{rank}(A^TA)=\mathrm{rank}A$ 。

證明請見“每週問題 October 19, 2009”。

(3) 若 $A^TA=0$ ，則 $A=0$ 。

性質 (3) 是性質 (2) 的必然結果。若 $A^TA=0$ ，則 $\mathrm{rank}A=\mathrm{rank}A^TA=\mathrm{rank}0=0$ ，惟有零矩陣其矩陣秩為零，推得 $A=0$ 。

Gramian 矩陣和正定矩陣有密切的關係 (見“特殊矩陣(6)：正定矩陣”)，歸結為以下三個性質。

(4) 對任一實矩陣 $A$ ， $A^TA$ 是半正定矩陣。

設 $\mathbf{x}\in\mathbb{R}^n$ 且 $\mathbf{x}\neq\mathbf{0}$ ，則

$\mathbf{x}^TA^TA\mathbf{x}=(A\mathbf{x})^T(A\mathbf{x})=\Vert A\mathbf{x}\Vert^2\ge 0$ 。

(5) 任一實對稱半正定矩陣 $M$ 皆可表示為 Grammin 矩陣，亦即存在一矩陣 $A$ 使得 $M=A^TA$ 。

實對稱矩陣 $M$ 可正交對角化為 $M=Q\Lambda Q^{T}$ (見“實對稱矩陣可正交對角化的證明”)，其中 $Q^TQ=I$ ， $\Lambda=\mathrm{diag}(\lambda_1,\ldots,\lambda_n)$ 。又 $M$ 為半正定，這意味對所有 $i$ ， $\lambda_i\ge 0$ ，故可令 $\Lambda^{1/2}=\mathrm{diag}(\sqrt{\lambda_1},\ldots,\sqrt{\lambda_n})$ 且 $A=\Lambda^{1/2}Q^T$ ，立得

$M=Q\Lambda Q^{T}=(Q\Lambda^{1/2})(\Lambda^{1/2}Q^T)=(\Lambda^{1/2}Q^T)^T(\Lambda^{1/2}Q^T)=A^TA$ 。

(6) 唯當 $A$ 的行向量 $\mathbf{a}_1,\ldots,\mathbf{a}_n$ 是線性獨立時， $A^TA$ 可逆，故為正定矩陣。

因為 $A$ 有線性獨立的行向量意味 $\mathrm{rank}A=n$ ，由性質 (2) 可知 $\mathrm{rank}(A^TA)=n$ ，反向陳述顯然成立。另外也可以考慮 $A\mathbf{x}=\mathbf{0}$ ，當 $A$ 有線性獨立行向量時，零空間 $N(A)=\{\mathbf{0}\}$ ，性質 (4) 的等號僅發生於 $\mathbf{x}=\mathbf{0}$ ，故 $A$ 為正定矩陣。

下面介紹 Gramian 矩陣的兩個化約形式。

(7) 任一 Gramian 矩陣 $G=A^TA$ 可表示為 $G=R^TR$ ，其中 $R$ 為上三角矩陣。

對於任意 $m\times n$ 階矩陣 $A$ ，求出 QR 分解 $A=QR$ ，其中 $m\times n$ 階 $Q$ 包含單範正交 (orthonormal) 行向量， $R$ 為 $n\times n$ 階上三角矩陣，將分解式代入計算可得

$G=A^TA=(QR)^T(QR)=R^TQ^TQR=R^TI_nR=R^TR$ 。

(8) 若 $A$ 有奇異值分解 $A=U\Sigma V^T$ ，Gramian 矩陣 $G=A^TA$ 可正交對角化為 $G=V\Lambda V^{-1}$ ，其中 $\Lambda=\Sigma^T\Sigma$ 。

利用奇異值分解性質 $U^{-1}=U^T$ ， $V^{-1}=V^T$ ，

$G=A^TA=(U\Sigma V^T)^T(U\Sigma V^T)=V\Sigma^TU^TU\Sigma V^T=V\Sigma^T\Sigma V^T$ 。

因為 $\Sigma$ 是奇異值 $\sigma_i$ 所構成的 $m\times n$ 階對角矩陣，且對於 $i=1,\ldots,r=\mathrm{rank}A$ ， $\sigma_i>0$ ，便有 $\Sigma^T\Sigma=\mathrm{diag}(\sigma_1^2,\ldots,\sigma_r^2,0,\ldots,0)$ 。

Gramian 矩陣還有下面這個有趣的性質。

(9) 假設對於任意同尺寸矩陣 $B$ ， $C$ ，下式皆可乘，則

$BA^TA=CA^TA~~~\Leftrightarrow ~~~BA^T=CA^T$ ，

$A^TAB=A^TAC~~~\Leftrightarrow ~~~A^TB=A^TC$ 。

考慮第一式，從右推至左陳述很容易， $BA^T=CA^T$ 同時右乘 $A$ 即可。從左推至右陳述需要運用一些代數技巧，寫出等式

$(BA^TA-CA^TA)(B^T-C^T)=(BA^T-CA^T)(BA^T-CA^T)^T$ ，

若上式等號左邊為零，由性質 (3) 可推論 $BA^T-CA^T=0$ 。使用相同方式亦可證得第二式，這留給讀者自行練習。

最後我們說明 Gramian 矩陣的行列式意義，詳細討論與證明請參閱“行列式的幾何意義”。

(10) 設 $A$ 為 $m\times n$ 實矩陣，Gramian 矩陣 $G=A^TA$ 的行列式等於 $A$ 的 $n$ 個行向量於幾何空間 $\mathbb{R}^m$ 所張開的平行多面體體積平方。

繼續閱讀：

利用 Gramian 矩陣證明行秩等於列秩

12 Responses to 特殊矩陣 (14)：Gramian 矩陣

levinc says:

03/27/2011 at 4:47 pm

這個form很常見，性質也常用，但我第一次知道原來它有個名字阿~~

ccjou says:

03/28/2011 at 9:41 am

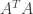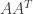是啊，多數教科書直接稱 $A^TA$ 和 $AA^T$ 為 cross-product matrix，大概不想再增加讀者的記憶負擔吧。

張盛東 says:

10/10/2014 at 6:36 am

周老師，請教一個問題。在Support Vector Machine中，為什麼一個valid的kernel function其Gramian Matrix必須是半正定矩陣呢？

- ccjou says:
  
  10/10/2014 at 8:31 am
  
  Mercer’s Theorem 可以回答你的問題，請見下文(1.2)：
  
  Click to access lecture7_notes.pdf
  
  - 張盛東 says:
    
    10/11/2014 at 9:06 am
    
    謝謝老師回答。
    
erofish says:

11/10/2015 at 5:41 pm

老师您好！非常喜欢您在博客上讲述的与线代有关的知识。最近学习数值分析的课程遇到了Gram矩阵，书上仅仅从内积空间的4个性质(正定，齐次，分配，交换)就证明了Gram矩阵行列式不为0的充要条件是v1,v2,…vn线性无关。我自己做推导却怎么也推不出来。不知道您能否在这篇博文里面讲的更加详细一点，谢谢！

- ccjou says:
  
  11/10/2015 at 7:15 pm
  
  近日我再另文回覆。
  
  (已回覆：
  
  答erofish──關於 Gramian 行列式不為零的充要條件
  
三石 says:

06/20/2017 at 12:21 am

老师您好，感谢您的这个网站。帮助非常大。学习了很多没注意到和不了解的线性代数知识。
这里请教下，这个gram矩阵有什么意义么？就是说在应用中或者机器学习控制论等等方面，运用gram矩阵的什么性质的到什么有用的结论呢？

问的比较宽泛，望您不吝赐教。
谢谢

- ccjou says:
  
  06/21/2017 at 10:58 am
  
  Gramian matrix應用廣泛，請參考維基百科
  https://en.wikipedia.org/wiki/Gramian_matrix#Applications
  或使用上文末的Gramian 矩陣標籤查詢本站貼文
  
  - 三石 says:
    
    06/29/2017 at 8:34 pm
    
    非常感谢老师
    
Gary Won says:

01/06/2019 at 1:50 am

老師您好，謝謝您寫出這麽好的頁面。
我這裏有一些小細節沒有處理好，請問在證明（9）的第二個式子的時候，我處理時左右乘（B^T-C^T),得到的結論是AB=AC,怎樣處理才能得到(A^T)B=(A^T)C呢

Pingback: Gram矩阵-数据谷

	jianglong on Strassen 演算法──分治矩陣乘法
	jianglong on Strassen 演算法──分治矩陣乘法
	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明