本文的閱讀等級:初級
矩陣之所以成為研究線性變換的一個有效工具乃基於兩個事實:線性變換完全由基底的映射行為所決定,以及線性複合變換可表示為矩陣乘積 (見“線性代數的第一堂課──矩陣乘法的定義”)。本文運用這兩個性質來設計二維歐幾里得空間裡常用的一些幾何變換矩陣。
線性變換是一種數學函數,特別的是它具有移動向量空間的功能。不過線性變換有別於一般的函數,下面的定理清楚地呈現了線性變換特殊之處,雖然此定理是如此的基本,但卻常被學者忽略。
唯一基底映射定理:令 為一個定義於
的有限維向量空間,
為
的一組基底,又令
為定義於
的另一個向量空間,
是
中任何向量。存在唯一一個從
映至
的線性變換
使得
。
證明包含三個部份:首先從給定的條件定義出變換 ,接著證明
確實是一個線性變換,最後推論它是唯一的。欲證明存在一個線性變換
滿足
,考慮向量空間
中的任何一個向量
,存在唯一數組
使得
,
接著定義
。
按此方式, 中的每一個成員
必對應
中的
,代入
,由此定義可知
,
。欲證明
是一個線性變換,令
,
為任一純量,則
根據定義可得
並且有
因此, 確實是一個線性變換。最後證明唯一性。若
為
映至
的一個線性變換,並滿足
,
,對於任何向量
,就有
這指出 其實就是上面所定義的
,故證明存在唯一的線性變換
滿足
,
。
上述定理告訴我們線性變換 被任一組基底的像 (image) 唯一決定。考慮線性變換
。令
為
的標準基底向量 (
的第
元為
,其餘元為
),且
,
。對於
中任何向量
,若
,
本身即為參考標準基底的座標向量
,線性變換
可用矩陣乘法表達如下:
。
上式中 的每一個行向量 (column vector)
即為標準基底向量
的像
,我們稱
為線性變換
參考標準基底的表示矩陣:
。
下面我們利用這個基本性質來設計一些常見的 幾何變換矩陣:旋轉、鏡射 (reflection)、伸縮與切變 (shearing)。
旋轉
考慮以原點為中心的逆時針旋轉 (見圖一),設 為旋轉角度,單位向量
,
經旋轉成為
,
,故旋轉矩陣為
。
鏡射
令 為穿越原點的任意直線,其中
,見圖二。
令 ,則
和
正交,故
為
的一組基底。令線性變換
代表對直線
的鏡射,且滿足
,
。欲解出
和
,設
將上面兩式合併為矩陣形式
,
亦即
。
解出組合係數,
。
代入以上結果即得
對於直線 的鏡射矩陣即為
。
這個結果還可以加以化簡,
令 ,上式可寫為
,又稱作 Householder 矩陣,
為鏡射軸的單位法向量 (見“特殊矩陣(4):Householder 矩陣”)。
鏡射變換矩陣還存在另一種表達式。在不失一般性原則下,設 ,即
,推知
,故令
,
,其中
是
和
軸的夾角。利用二倍角公式,
鏡射變換矩陣亦可寫為
。
伸縮
伸縮可分別應用於 軸和
軸。若
軸伸縮
倍,
軸伸縮
倍,即
,
,伸縮矩陣即為對角矩陣
。
切變
切變有兩種可能的形式 (見圖三),平行於 軸的切變滿足
,
,切變矩陣為
,
平行於 軸的切變滿足
,
,切變矩陣為
。
較為複雜的變換可透過複合變換來實現,下面舉一例說明設計過程。考慮沿著穿越原點直線 方向伸縮
倍的線性變換
。令
,先執行旋轉
使
與
軸重合,沿著
軸伸縮
倍,最後再經過
把
轉回原方向,矩陣表達式如下:
然而,不論我們如何組合上述變換矩陣,都無法設計出「以平面上任意點 (非原點) 為中心的逆時針旋轉」或「對不穿越原點的直線鏡射」,其中原因在於這兩種變換都必須使用平移。考慮 任意向量
的平移運動
,因為
,故平移並非線性變換,也就是說,平移不能以矩陣來表示。為了克服這個問題,於是有齊次座標 (homogeneous coordinates) 和仿射 (affine) 變換的誕生,詳細討論見“仿射變換”。




周老师,您好!向您请教一个问题:
我们知道:1. 线性变换可以表示为矩阵的乘积;2. 矩阵的转置是一个线性函数;3. 不存在一个矩阵 ,使得对于任意一个矩阵
,使得对于任意一个矩阵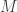 ,都有
,都有 ;
;
但若给定一个矩阵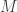 ,我们是否总能找到一个矩阵
,我们是否总能找到一个矩阵 ,使其满足
,使其满足 ?
?
而显然答案是否定的。考虑 ,满足该等式的
,满足该等式的 并不存在。
并不存在。
所以,我的疑问是既然矩阵转置是线性函数,而线性函数又可以表示为矩阵的乘积,但针对上述的特例,这样的矩阵却有可能不存在。“可以表示”和“有可能不存在”这两者是否互为矛盾,或者这二者之间存在怎样的一种联系?
注:示例等号右端的显示不正确,应为左侧矩阵 的转置
的转置
所以,是否可以说:“线性变换并不总是能表示为矩阵的乘积,因为这样的矩阵可能并不存在”
我要想一想這個問題,他日另文回覆。
LaTeX語法已訂正,現可正確顯示。
已回覆: