本文的閱讀等級:中級
上文“傅立葉級數 (上)”介紹了 -週期實函數
的傅立葉級數
為餘弦和正弦函數組成的無窮級數:
,
其中傅立葉係數 和
的計算公式如下:
若 是一奇函數,則
,故
,
。另一方面,若
是一偶函數,則
,故
,
。
-週期函數的傅立葉級數
考慮一週期等於 ,定義於區間
的週期函數
。利用變數變換
可使區間
變換至
,將
代入
,即得到
的傅立葉級數:
,
將 代入
的傅立葉係數的積分公式,可得
對於 -週期函數
,任何區間
皆可使用,如何選擇
值取決於便利性和個人偏好,常見的設定有
或
。
指數傅立葉級數
傅立葉級數包含餘弦和正弦兩種函數。利用歐拉公式 ,其中
,我們可以寫出更為精簡的傅立葉級數表達式。首先察覺
和
可用
表示成
,
再將傅立葉級數 中
和
的線性組合式改寫如下:
上式令 和
的係數分別為
。
若 ,就有
。將以上結果代回
-週期函數
的傅立葉級數即得指數傅立葉級數:
。
因為實函數 的傅立葉係數
和
都是實數,可知
,故對於每一
,複傅立葉係數
有相同的計算公式:
。
類似地,-週期函數
的指數傅立葉級數如下:
,
複傅立葉係數則為
。
如果打從一開始考慮指數函數集 ,運用上文所述傅立葉級數推導程序也可以導出
-週期實函數
的指數傅立葉級數。基本想法是將
正交投影至集合
擴張出的子空間上,但
是複指數,因此實函數的內積定義必須修改為複函數內積。對於區間
的兩複函數
和
,我們定義其內積如下 (內積必須滿足的條件請見“內積的定義”):
,
可知 的「長度」或範數 (norm) 為
複函數內積引入常數 的用意在使
成為一個單範正交 (orthonormal) 函數集。將上文得到的積分結果整理出來:
其中 是 Kronecker 函數:
若
,
若
。利用上述性質立得
因此證明 是一個單範正交集。函數
的指數傅立葉級數即為
至
擴張成的子空間的正交投影:
,
正交分解所含的係數就是複傅立葉係數:
。
上面的推導過程並未假設 是實函數,事實上,指數傅立葉級數同樣適用於
-週期的複函數。但是當
是複函數時,不能保證
和
是共軛複數,這是唯一要注意的差別。
Parseval 定理
若 為一有限維向量空間,
是
的一組單範正交基底,則
中任一向量
的長度與其正交分解展開式
的係數
之間具有以下簡單關係:
複傅立葉係數 與其所描述的
-週期函數
之間也有類似關係,稱為 Parseval 定理:
。
當 ,
,且
,故複傅立葉係數平方和亦可寫為
。
下面證明 Parseval 定理。上文曾經指出整個傅立葉級數 收斂至
,即
,也就有
,由此可導出
最後舉一個 Parseval 定理的應用例子:計算無窮級數 。考慮定義於區間
的函數
,因為
是偶函數,
,故僅須計算
,結果如下:
且 ,則
的傅立葉級數為
。
計算 Parseval 定理等號左邊:
,
再計算 Parseval 定理等號右邊:
,
比較等號兩邊即得
。
傅立葉級數成功地將週期函數分解為無窮多個餘弦和正弦函數的線性組合,如欲將傅立葉級數推廣至非週期函數,最直接的方法是將所處理的函數定義於無限大區間 (且無任何特殊週期),如此得到的分解表達式稱為傅立葉轉換 (Fourier transform),這是下一回我們要討論的主題。

原来引入欧拉公式表示复数域最终剩下的依然只有实数域,只是一些表达上的tricks。
老師您好! 最近在複習傅立葉級數,覺得受益良多! 用Parseval定理
用Parseval定理
關於最後在算
為什麼會知道要用這個方法呢?
因為看完算式過程,腦中第一個想法是:天阿怎麼想到的
會有一種是”湊”出來的感覺,不過有可能是小弟資質不足QQ
另外函數f(t)=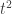 跟對應區間,如果換成不同函數或是不同區間
跟對應區間,如果換成不同函數或是不同區間
還能這樣算嗎?
應該說我真正好奇的是這題目如何被設計出來的…
不好意思還不太會用這語言..