本文的閱讀等級:初級
公元1990年德國 Springer Verlag 出版公司發行的 The Mathematical Intelligencer 期刊公布一項票選結果:歐拉恆等式 (Euler’s identity) 獲選為「最優美的數學定理」(the most beautiful theorem in mathematics)[1]。下面抄錄維基大典的歐拉生平介紹[2]:
歐拉 (Leonhard Euler),瑞士巴塞爾人也,一七零七年四月十五日生。一七二六年得博士銜。翌年,教俄羅斯科學院,俄與數學競賽,論船桅之構作,僅敗於布給。布給者,泰西航海學之父也。越四年,除教授。復越兩年,拜數學系主任。翌年,罹患,右目眇。一七四一年,俄國亂,遂遷柏林,教柏林科學院。一七六六年,返俄羅斯科學院。一七八三年九月十八日卒,年七十七。法蘭西哲人孔多塞曰:「至此,歐拉不復算數,亦無復生也。」歐氏執十八世紀數學牛耳,論文近千,惟二十世紀保羅•艾狄胥可匹敵之。究分析,創函數,混一歐洲大陸及英國之微積分;解七條橋問題,開圖論及拓撲之先;論複數,究歐拉數,得歐拉恆等式,譽最優美恆等式;論凸多面體,證歐拉等式,後人推而廣之,得流形之歐拉特徵值;究歐拉函數,得歐拉定理,為費馬小定理之推廣。

Leonhard Euler (1707-1783) From http://plus.maths.org/issue42/features/wilson/Euler_1_web.jpg
這是著名的歐拉恆等式:
,
其中 是自然對數的底數,亦稱歐拉數,
是虛數單位,滿足
(或寫成
),
是圓周率。歐拉恆等式出現三個基本算術運算:加法、乘法與指數,聯繫了五個基本數學常數:
。歐拉恆等式是歐拉公式 (Euler formula) 的一個必然結果,它說:
,
其中 為任意實數。根據歐拉公式,指數函數
的實數部分等於餘弦函數
,虛數部分等於正弦函數
。在複數平面上,
位於單位圓周,
即為從
至
的 (有號) 弧長 (見圖一)。當
,即得歐拉恆等式。
美國麻省理工學院 (Massachusetts Institute of Technology,簡稱 MIT) 斯傳 (Gilbert Strang) 教授在他的線性代數教科書裡講述了一個關於歐拉公式證明的故事[3]:
我還記得 MIT 收到一名紐約囚犯來信的那一天,他詢問歐拉公式是否為真。當你一想到這個公式優美地將三個基礎數學函數聯繫在一起時,不免感到驚訝。我們的最佳解答是檢視冪級數
,
其中實數部分
是餘弦,虛數部分
是正弦。這個公式是正確的,我希望當時我們寄了一個更優美的證明。
除了 MIT 寄出的泰勒展開式 (Taylor expansion) 證法,我們也可以用極限定義和微分學來證明[4]。指數函數 定義如下:
。
代入 ,並考慮數列
當 ,
趨於
。見圖二,當
,
的角度和長度分別為
,
,
其中 表示誤差。所以,
從
啟始,角度旋轉了
,長度伸縮了
。當
,利用上面兩式,可得
,
,
也就證明當 ,
趨於
。
下面說明歐拉公式的微分學證法。寫出 的極座標表達式
,
其中 與
為實數。求等號兩邊導數,可得
。
將 代回等號左邊
並整理等號右邊,
。
比較等號兩邊實部和虛部,可得 和
。當
,
,可知
和
有初始值
和
,合併以上結果可推論
且
,故證得所求。
德國數學家高斯 (Carl Friedrich Gauss) 曾說[1]:「如果一個學生在被告知歐拉公式時未能立刻視之為明顯的事實,這個學生將來絕不會是一流的數學家。」讀了 MIT 提供的證明後,那名囚犯是否因此相信歐拉公式是真確的?會不會如小說或電影情節那樣,囚犯日後成為一位一流的數學家?斯傳沒有透露後續故事。那麼聽聞歐拉公式後,一般菁英學者又有什麼反應呢?從十九世紀美國哈佛大學數學教授皮爾斯 (Benjamin Peirce) 在講堂證畢歐拉恆等式之後所說的這段話,不難想像當第一次面對史上最優美的數學定理時,多數的學生是何等茫然與困惑[5]:
各位先生,它一定是真實的,它絕對是詭奇的。我們不了解它,我們也不明白它的含意。但我們已經證明了這個公式,所以我們知道它必定是正確的。
註解
[1] http://en.wikipedia.org/wiki/Euler’s_identity
[2] 維基大典的歐拉生平介紹
[3] Gilbert Strang, Linear Algebra and its Applications, third edition, Harcourt Brace Jovanovich, pp 185, 1988. 原文如下:“I remember the day when a letter came to MIT from a prisoner in New York, asking if Euler’s formula was true. It is really astonishing, when you think of it, that three of the key functions of mathematics should come together in such a graceful way. Our best answer was to look at the power series . The real part
is the cosine. The imaginary part
is the sine. The formula is correct, and I wish we had sent a more beautiful proof.”
[4] http://en.wikipedia.org/wiki/Euler%27s_formula
[5] 原文是 “Gentlemen, that is surely true, it is absolutely paradoxical; we cannot understand it, and we don’t know what it means. But we have proved it, and therefore we know it must be the truth.”



以前在一本書上,看到簡潔之證明:





在書上, 以高斯平面坐標繪圖表示,而前面的微分方程,推演出圓周旋轉的
以高斯平面坐標繪圖表示,而前面的微分方程,推演出圓周旋轉的 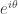
這種證明過程,也是很有趣!
書上說一開始 和
和 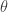 的關係為何?是不是
的關係為何?是不是  ?假設是這樣,就有
?假設是這樣,就有  ,最後一個步驟取自然指數得到
,最後一個步驟取自然指數得到  ,接著必須證明
,接著必須證明 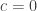 。有人可能以為令
。有人可能以為令 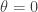 ,
, ,故
,故 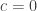 。但這離結果還有一段距離,因為
。但這離結果還有一段距離,因為  是複數,
是複數, 並不僅有唯一解
並不僅有唯一解 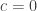 。事實上,歐拉公式告訴我們
。事實上,歐拉公式告訴我們  的解包括
的解包括  ,
, 。歐拉公式的證明重點在於釐清 exp, sin, cos 的定義,特別是在複數域的定義。
。歐拉公式的證明重點在於釐清 exp, sin, cos 的定義,特別是在複數域的定義。
說到微分方程,還有一個快捷證法。考慮 ,
,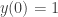 。不難確認
。不難確認 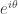 和
和  都為其解,唯一定理說明兩者相等。
都為其解,唯一定理說明兩者相等。
大約民國77年,我在台北重慶南路逛書店,無意中翻閱一本書,看到歐拉公式以解微分方程,得到證明。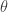 的關係為何?我不記得。
的關係為何?我不記得。 。」
。」
那本書我沒買,經過二十多年,腦子裡還有一些印象。
而書中一開始z和
—————————————————————————
歐拉公式,真的讓我感覺很有趣,曾經用很多時間,想要探求其中奧妙,但我不是唸理工科系,所以只有學到一小部分。
最初是在民國73年,我高中一年級,因為參加電腦研習社,而認識高二學長王才沛,有一天他說:「世界上最優美的數學式就是
我未能立刻視之為明顯事實,思索好幾個月,皆不懂這條數學式。
等我升上高二,由cos及sin的泰勒展開式,聯想、推敲,得到歐拉公式的證明,心裡很高興。
高三微積分課程,老師有教cos及sin的泰勒展開式,我高二是在電腦程式設計的書看到泰勒展開式。
高中畢業,去台北補習,準備重考大學,星期日沒課,逛書店看到不同方式證明歐拉公式,真的印象深刻!
印象中,那本書上,以圖形表示,畫個圓,圓上有一小段弧,弧之切線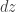 :
:
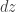 的長度,是半徑
的長度,是半徑  乘以
乘以  ,
,
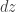 的方向,是由
的方向,是由  左旋90度,所以要乘上
左旋90度,所以要乘上  。
。
因此
真佩服你的記憶力!說來慚愧,我完全想不起來第一次聽聞歐拉公式是甚麼時候,大一微積分?大二複變?這說明當時我對這個史上最優美的數學定理……無感。
高斯的評論是精準的。
雖然 Euler 是偉大的數學家 但面對有關”人”方面的問題就束手無策,只能興嘆”人比數學更複雜”!
一直覺得尤拉公式的證明有一個很神奇的地方
在我們還不知道複數的極限,微分,積分,泰勒展開是否完全遵照實數規則走的時候
我們就把它套用上去了
甚至我們是用這條公式去對虛數指數函數進行定義
學習複變函數的時候,也是直接用尤拉公式往下推演
這也許是我讀的是工程數學的複變函數而並非是數學系正統複變函數論的原因
所以我一直在懷疑這最基本的基石究竟合不合理?
我在處理這些部分的時候,是直接將尤拉公式當成定理用背的
latex \sum \limits{a + b + c = n} \frac{n!}{a! b! c!} x^a y^b z^c$
i是常数,但不属于R,因此,对等号两边使用全微分公式(人类在未发明i时,该公式对实数成立)时,di如何处理,它一定=0?
Pingback: 傅立葉分析及應用 Fourier Analysis and Applications | 個人認為好的個人認為好的
Pingback: EulerAngle – 專題、人際、生活、文字語言