本文的閱讀等級:中級
在統計學中,我們感興趣的全部個體或項目所成的集合稱為母體 (population),譬如,某農場的羊群,某國家的人民。母體的一個未知或已知數值稱為參數 (parameter),通常用來定義統計模型,譬如,某農場羊寄生蟲的發病率,某國家人均所得變異數。為了估計母體的參數,我們從母體選出一組個體或項目稱為樣本 (sample)。只要不含未知參數,任何一個由樣本數據構成的函數都稱為統計量 (statistic)。所以參數用於母體,統計量則用於樣本。本文介紹線性代數觀點下的三個統計量:樣本平均數 (sample mean),樣本變異數 (sample variance) 和樣本共變異數 (sample covariance)。
假設我們從調查或實驗中獲得一組樣本數據 ,一般人最先想到的統計量是集中趨勢測度,也就是這組數據的中心值或典型值,設為
。我們用一個誤差函數來測量單一數值
代表整組數據
的適合性。在統計學與工程應用中,均方誤差 (mean squared error) 是最常被採用的誤差函數,如下:
其中 是樣本數據構成的實向量,
。樣本數據
是從母體抽取的
個觀測值,或視為
空間的一個點,從這個幾何觀點得以切進線性代數。理想的中心值
應該具有最小的均方誤差,而此最小均方誤差值可用來表示樣本的離散 (偏離中心值) 趨勢。稍後我會解釋為何均方誤差不除以樣本數
,而是除以
,但不論除以哪個 (非零) 常數都不會改變使誤差函數最小化的中心值。至少有三個方法可解出使
最小化的
值:根據基礎微分學,最小均方誤差發生於
[1];從幾何直覺下手,正交原則給出最小均方誤差的一個充要條件;在幾何座標空間
中,當
等於
在直線
的正交投影時,
有最小值 (見圖一)。
令 表示滿足最小化均方誤差的
值。投影後的殘餘量
與直線
的指向向量
正交,即
,
因此可得
,
稱為樣本平均數。另外,僅使用代數亦可證明 最小化
[2]。投影殘餘量
的第
元,
,表示數據點
相對平均數
的偏離量,稱為離差 (deviation)。最小均方誤差即為均方離差,可用來測量整組數據相對平均數的離散程度,稱為樣本變異數,表示如下:
。
離差向量 屬於子空間
的正交補餘 (orthogonal complement),標記為
,即所有與
正交的向量所形成的集合 (見“正交補餘與投影定理”)。因為
是
的一個超平面 (hyperplane,見“超平面”),
,可知
只能在
維的子空間內「活動」。統計學的說法是離差集合
有
個自由度 (degrees of freedom)。
為甚麼樣本變異數要除以自由度 ,而非樣本數
?令
為子空間
的一組單範正交基底 (orthonormal basis),意思是每一
是單位向量,且任意
和
,
,彼此垂直 (正交)。離差向量
可唯一表示成
的線性組合:
。
因為 若
,且
若
,就有
樣本變異數可改寫為
,
其中 是任意的
個數,由此可知均方離差 (即樣本變異數) 除以自由度
不僅合理而且公允。
接下來討論包含兩個變數的樣本數據 。針對變數
和
,樣本平均數為
,
樣本變異數為
。
為了測量變數 和
的關連性,我們可以仿造樣本變異數的形式定義樣本共變異數,如下:
,
上式中 等於平面上兩對角端點
和
構成的長方形 (有號) 面積:若
在第一或第三象限,面積為正;若
在第二或第四象限,面積為負。圖二中,座標原點為
,藍色長方形面積為正,紅色長方形面積為負,所有面積的平均數 (除以
) 即為樣本共變異數。
共變異數和變異數同樣除以自由度 ,而非樣本數
,理由如下。令
和
。樣本共變異數可表示為
。
將 和
寫成
的線性組合:
計算內積可得
可知共變異數即為 的平均數,因此除以自由度
至為明顯。
從定義上看,共變異數 是離差乘積
的均值,這代表什麼意義?類似平均數的推演過程,考慮以直線
近似
,則有下列均方誤差:
。
使 最小化的係數
必須滿足正規方程 (見“曲線配適”),即
。
運用代數技巧化簡係數矩陣,設 ,並將誤差函數改為
,
其正規方程如下:
。
上式等號兩邊同除以 ,並代入已知關係,就有
,
解出 ,即得
,最佳配適直線為
。
接著算出對應的最小均方誤差:
其中
稱為相關係數 (correlation coefficient)。因此,最佳配適直線亦可表示為
。
不難驗證相關係數 即為
和
夾角
的餘弦 (見“相關係數”)
,
因此 。若
,我們說
和
無相關,變數
不具備預測
的能力,這時
的均方誤差等於其樣本變異數
。若
,藉由最佳配適直線
,
的均方誤差減少了
。由於
的加入,
決定
的均方誤差減少的比例,故
也稱為決定係數 (coefficient of determination)。
本文從線性代數觀點推導樣本平均數、變異數與共變異數。從統計學觀點,由多變量常態分布的最大似然估計 (maximum likelihood estimation) 亦可推得同樣結果 (樣本變異數與共變異數的最大似然估計可調整為無偏估計),詳見“多變量常態分布的最大似然估計”。
註解
[1] 令 表示使得均方誤差
最小化的
值。對均方誤差
求導,
令上式為零,即解出 。
[2] 令 。寫出
根據 的定義,上式最末一項為零,即知
。
這表明 ,等號於
時成立,故得證。



看完這篇,有種萬物同源的感覺.
或者這麼說:線性代數已佔據應用數學的中心地帶。
正在修數理統計。這篇佳作 comes just in time.
(1) 自由度 n-1 有沒有更 intuitive 的解釋?
(2) 有沒有類似文章的參考?
(1) 就我個人而言,線性代數觀點(或者說幾何觀點)是最具直覺的解釋。一般統計學常見的說法是這樣: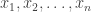 共有
共有  個自由度,扣除樣本平均數
個自由度,扣除樣本平均數  此一個限制後,剩下
此一個限制後,剩下 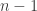 個自由度。或者說,你可以隨意選擇
個自由度。或者說,你可以隨意選擇  ,但是最後
,但是最後 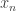 僅有唯一選擇,因為要符合平均數是
僅有唯一選擇,因為要符合平均數是  此一限制。
此一限制。
(2) http://www.math.uah.edu/stat/index.html
請見 5. Random samples
25年前,我在高中時期,也曾經思考「自由度」為何是 n-1 ?
假如 n 很大, n 與 n-1的差別不顯著。
若 n=3,舉個例子:7, 8, 9三個數字,平均值為8,
7與8差1,
9與8也是差1,
直覺看來,標準差是1。
上例當中,7, 8, 9三個數字,使用計算標準差的公式,除以 (n-1) ,恰好得到與直覺相同的答案。
當年,聽高中老師講「自由度」,實際上,我沒聽懂,也不敢在課堂上發問,只好自己擬個「直覺」方法。不知其他同學的看法如何?高中課程,進度很趕,學生能夠記住公式,就很好了!大概沒有多餘的時間去探究「為什麼?」
現在看到大俠解說,心裡多年的疑問,算是得到釋懷。
David Salsburg 寫了一本科普著作:The lady tasting tea: how statistics revolutionized science in the 20th century,中譯《統計改變了世界》,2001,天下文化出版,其中67頁說道:「自由度的新觀念」是費雪(英國統計學家)發現的,這與他特有的幾何洞察力,以及他把數學問題轉化成多維空間幾何的能力有直接關係。
我猜費雪所稱的自由度應該源於線性代數的子空間維度。或許目前修我的研究所課程的學生中也有些人仍不明白自由度是甚麼意思。
老师,关于除以(n-1)的部分,我有一点不明白,希望您能帮我解答一下。您给出的(n-1)个自由度的解释,是不是说,其实这个变异数是在(n-1)个方向上的平均值? ,变异数为
,变异数为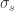 ,对
,对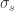 求期望,如果用
求期望,如果用 来统计的话,那么
来统计的话,那么 是不等于
是不等于  ,也就是实际数据的分布的,所以才要除以(n-1),对于这种解释,老师您怎么看?
,也就是实际数据的分布的,所以才要除以(n-1),对于这种解释,老师您怎么看?
另外,我之前也因为这个问题纠结了很久,之前查资料的到的结果是,对于采样数据对数据整体进行估计的话,记样本均值为
我参考的资料来自:
Click to access Proof%20that%20Sample%20Variance%20is%20Unbiased.pdf
我將你的迴響編輯過以正確顯示LaTeX,方式是在LaTex語言,如 \mu,之前加入符號$latex並填入一空格,之後再以符號$結束,即呈現 。
。
從幾何角度來看,除以(n-1)的原因是離差位於一個維度等於(n-1)的子空間(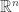 的超平面),所以真實的自由度(無限制的變數數目)僅有(n-1)。這就是你說的(n-1)個方向,只是線性代數稱為維度等於(n-1)的子空間,或者由(n-1)個基底向量擴張的子空間。
的超平面),所以真實的自由度(無限制的變數數目)僅有(n-1)。這就是你說的(n-1)個方向,只是線性代數稱為維度等於(n-1)的子空間,或者由(n-1)個基底向量擴張的子空間。
一般統計學的解釋這樣的:你已經知道平均數 ,你可以任意選擇
,你可以任意選擇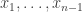 ,但
,但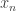 必定等於
必定等於 ,所以你擁有的自由度是(n-1)。
,所以你擁有的自由度是(n-1)。
從參數估計來看,如果樣本變異數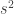 (它隨著樣本改變,故可視為一個隨機變數)的期望值
(它隨著樣本改變,故可視為一個隨機變數)的期望值![E[s^2]](https://s0.wp.com/latex.php?latex=E%5Bs%5E2%5D&bg=ffffff&fg=333333&s=0&c=20201002) 等於母體參數,即變異數
等於母體參數,即變異數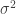 ,則該估計稱為無偏估計(unbiased estimator),否則稱為有偏估計。最大可能性(maximum likelihood)給出的變異數估計是
,則該估計稱為無偏估計(unbiased estimator),否則稱為有偏估計。最大可能性(maximum likelihood)給出的變異數估計是 ,但它是一個有偏估計,因為
,但它是一個有偏估計,因為![E[\hat{\sigma}^2]=\frac{n-1}{n}\sigma^2](https://s0.wp.com/latex.php?latex=E%5B%5Chat%7B%5Csigma%7D%5E2%5D%3D%5Cfrac%7Bn-1%7D%7Bn%7D%5Csigma%5E2&bg=ffffff&fg=333333&s=0&c=20201002) 。所以如果我們希望的是無偏估計,那麼要選擇
。所以如果我們希望的是無偏估計,那麼要選擇 。證明如下:
。證明如下:
![E[s^2]=\frac{1}{n-1}E[\sum_{i}x_i^2-nm^2]=\frac{1}{n-1}(\sum_iE[x_i^2]-nE[m^2])=\frac{1}{n-1}(\sum_i(\sigma^2+\mu^2)-n(\sigma^2/n+\mu^2))=\sigma^2](https://s0.wp.com/latex.php?latex=E%5Bs%5E2%5D%3D%5Cfrac%7B1%7D%7Bn-1%7DE%5B%5Csum_%7Bi%7Dx_i%5E2-nm%5E2%5D%3D%5Cfrac%7B1%7D%7Bn-1%7D%28%5Csum_iE%5Bx_i%5E2%5D-nE%5Bm%5E2%5D%29%3D%5Cfrac%7B1%7D%7Bn-1%7D%28%5Csum_i%28%5Csigma%5E2%2B%5Cmu%5E2%29-n%28%5Csigma%5E2%2Fn%2B%5Cmu%5E2%29%29%3D%5Csigma%5E2&bg=ffffff&fg=333333&s=0&c=20201002)
有空時我再另外寫些關於最大可能性估計的介紹。
谢谢回复
您的意思是不是说这两种做法是同一个问题的两种角度,而他们的结论是一致的?
是的。這麼說吧,有些事情因為講者與聽者不屬於同一社群(因此沒有共同的認知與信仰),講者只好發明多種支持其信念的論述。「平均量」意味等分配給群體中的所有個體,所以先要確定群體中的個體總數。但甚麼才是真實的個體總數呢?英國統計學家費雪說:自由度,即可以任意改變的變數總數,就是線性代數說的子空間維度。他們聲稱:樣本變異數必須除以(n-1)。另外一批人認為無偏估計才是理想的估計方法,剛巧他們發現 是變異數的無偏估計,故認可除以(n-1)是正確的。於是,這倆批人擁抱在一起──取暖也。此後世人漸漸接受了這個論點,有人索性將這些說法寫入課本,很久以後,大家便習以為常視之為真理,除非有一天發生科學革命。大致上,這就是孔恩(Thomas Samuel Kuhn)的看法。
是變異數的無偏估計,故認可除以(n-1)是正確的。於是,這倆批人擁抱在一起──取暖也。此後世人漸漸接受了這個論點,有人索性將這些說法寫入課本,很久以後,大家便習以為常視之為真理,除非有一天發生科學革命。大致上,這就是孔恩(Thomas Samuel Kuhn)的看法。
我明白了! 谢谢您的耐心回复!从来没有得到这么详细而且生动的解释,再次感谢~
晚上多喝了幾杯啤酒,扯遠了。昨天紐約時報有篇報導:「啤酒有利於共建『文明社會』」
http://cn.nytimes.com/article/life-fashion/2013/04/16/c16beer/zh-hk/
裡面說:「有了這種全新的精神藥理學飲品,人類就可以壓制自己違背群體本能的焦慮。」起初(很久很久以前)我對於除以(n-1)這件事也很感冒(違背統計學家群體的焦慮),漸漸也就習以為常,不以為意。所以說,革命是年輕人的事。
哈哈哈,啤酒是好东西啊~黄汤下肚,烦恼全无啊。。。我喜欢开心的时候喝酒,不爽的时候反倒忍住不喝了,譬如前几天被女朋友甩了,哈哈哈,反倒觉得心情不好喝酒倒像是逃避了~其实有很多细枝末节的小问题,小学初中高中这么一路背下来了,到了研究生这会才算是真正搞清楚,哈哈,比起许多从小打好基础的人来说,我也已经老了。曾经也想就这么一直糊涂下去算了,但是后来想想,如果真要搞研究的话,遇到每一个问题都要搞清楚~革命不容易啊~不过看到有像老师这样不辞辛苦,写博客普及纯粹的数学知识的人,我心里才是真的佩服呢~
謝謝,佩服不敢當。不過老實說,眾多讀者的鼓勵才是我持續寫下去的最大動力。先這樣了,老婆喊我去洗碗(還有收酒瓶)。
這篇文章寫的好讚啊
當mu =(x1+x2+…+xn)/n 確定後,x1, x2, …x n就只能有(n-1)個可變,當然就只有(n-1)個維度。
說明是(n-1)個維度之後,then so what