線性變換與矩陣的用語比較

本文的閱讀等級：初級

在線性代數中，線性變換 (或稱線性映射) 是矩陣的一種抽象描述，矩陣則為線性變換的具體實現。令 $T:\mathcal{V}\to\mathcal{W}$ 是一個從向量空間 $\mathcal{V}$ 映至向量空間 $\mathcal{W}$ 的變換，其中 $\mathcal{V}$ 稱為定義域 (domain)， $\mathcal{W}$ 稱為到達域 (codomain)。每一個向量 $\mathbf{x}\in\mathcal{V}$ 經由 $T$ 映至到達域 $\mathcal{W}$ 的一個向量 $T(\mathbf{x})$ ，稱為 $\mathbf{x}$ 的像 (image)。對於任何 $\mathbf{x},\mathbf{y}\in\mathcal{V}$ 與純量 $c$ ^[1]，如果 $T$ 滿足兩個條件

$\begin{aligned} T(\mathbf{x}+\mathbf{y})&=T(\mathbf{x})+T(\mathbf{y})\\ T(c\mathbf{x})&=cT(\mathbf{x}),\end{aligned}$

則 $T$ 稱為一個線性變換。若 $\mathcal{V}=\mathcal{W}$ ， $T:\mathcal{V}\to\mathcal{V}$ 也稱為線性算子 (linear operator)。假設 $\mathcal{V}$ 和 $\mathcal{W}$ 是有限維向量空間， $\dim\mathcal{V} = n$ 且 $\dim\mathcal{W}=m$ 。令 $\boldsymbol{\beta}$ 和 $\boldsymbol{\gamma}$ 分別為向量空間 $\mathcal{V}$ 和 $\mathcal{W}$ 的基底。任一線性變換 $T:\mathcal{V}\to\mathcal{W}$ 可用矩陣乘法表示如下 (見“線性變換表示矩陣”)：

$\begin{bmatrix} T(\mathbf{x}) \end{bmatrix}_{ \boldsymbol{\gamma}}=\begin{bmatrix} T(\boldsymbol{\beta}) \end{bmatrix}_{\boldsymbol{\gamma}}\begin{bmatrix} \mathbf{x} \end{bmatrix}_{\boldsymbol{\beta}}$ ，

其中 $\begin{bmatrix} \mathbf{x} \end{bmatrix}_{\boldsymbol{\beta}}$ 是向量 $\mathbf{x}\in\mathcal{V}$ 參考 $\boldsymbol{\beta}$ 的 $n$ 維座標向量， $\begin{bmatrix} T(\mathbf{x}) \end{bmatrix}_{\boldsymbol{\gamma}}$ 是像 $T(\mathbf{x})\in\mathcal{W}$ 參考 $\boldsymbol{\gamma}$ 的 $m$ 維座標向量， $\begin{bmatrix} T(\boldsymbol{\beta}) \end{bmatrix}_{\boldsymbol{\gamma}}$ 稱為線性變換 $T$ 參考基底 $\boldsymbol{\beta}-\boldsymbol{\gamma}$ 的 $m\times n$ 階表示矩陣。反過來說，給定 $m\times n$ 階複矩陣 $A$ ， $T(\mathbf{x})=A\mathbf{x}$ 是一個從 $\mathcal{V}=\mathbb{C}^n$ 映至 $\mathcal{W}=\mathbb{C}^m$ 的線性變換，因為對於 $\mathbf{x},\mathbf{y}\in\mathbb{C}^n$ 與 $c\in\mathbb{C}$ ，

$\begin{aligned} A(\mathbf{x}+\mathbf{y})&=A\mathbf{x}+A\mathbf{y}\\ A(c\mathbf{x})&=cA\mathbf{x}.\end{aligned}$

因此，矩陣與定義於有限維向量空間的線性變換可謂一體兩面。儘管線性變換和矩陣講述的是同一件事 (精確的說法是同構，見“同構的向量空間”)，但它們卻有各自的專用術語，下面分別就子空間、維數和映射性質加以說明比較。

線性變換

線性變換 $T:\mathcal{V}\to\mathcal{W}$ 有兩個重要的子空間：值域 (range) 與核 (kernel)。值域 $R(T)$ ，或記為 $\text{ran}(T)$ 或 $\text{im}(T)$ ，是 $T$ 的所有像所形成的集合，

$R(T)=\{T(\mathbf{x})\vert\mathbf{x}\in\mathcal{V}\}$ ；

而核 $\mathrm{ker}(T)$ 是 $T$ 所消滅的向量所形成的集合，

$\mathrm{ker}(T)=\{\mathbf{x}\in\mathcal{V}\vert T(\mathbf{x})=\mathbf{0}\}$ 。

不難證明 $R(T)$ 是到達域 $\mathcal{W}$ 的一個子空間， $\mathrm{ker}(T)$ 是定義域 $\mathcal{V}$ 的一個子空間，兩者的維數具有下列關係 (見下圖)：

$\dim\mathcal{V}=\dim\mathrm{ker}(T)+\dim R(T)$ ，

其中 $\mathrm{rank}T=\dim R(T)$ 稱為 $T$ 的秩 (rank)， $\mathrm{nullity}T=\dim\mathrm{ker}(T)$ 稱為 $T$ 的零度 (nullity)，故上式也稱為秩—零度定理 (見“線性代數基本定理 (一)”)。

值域、核與秩─零度定理

我們可以根據子空間的映射界定線性變換的一些性質：

若 $R(T)=\mathcal{W}$ ，即 $\mathrm{rank}T=\dim\mathcal{W}$ ，值域充滿整個到達域， $T$ 稱為滿射 (onto 或 surjective)。
若對於任意 $\mathbf{x}\neq\mathbf{y}$ ，恆有 $T(\mathbf{x})\neq T(\mathbf{y})$ ，或者說 $T(\mathbf{x})=T(\mathbf{y})$ 蘊含 $\mathbf{x}=\mathbf{y}$ ，則 $T$ 稱為一對一 (one-to-one) 或單射 (injective)。下面是我們經常使用的一對一界定性質：若 $\mathrm{ker}(T)=\{\mathbf{0}\}$ ，則 $T$ 是一對一，反之亦然。理由如下：設 $\mathrm{ker}(T)=\{\mathbf{0}\}$ 。若 $T(\mathbf{x})=T(\mathbf{y})=\mathbf{b}$ ，則 $T(\mathbf{x}-\mathbf{y})=T(\mathbf{x})-T(\mathbf{y})=\mathbf{b}-\mathbf{b}=\mathbf{0}$ ，故 $\mathbf{x}=\mathbf{y}$ ，證得 $T$ 是一對一。反之，設 $T$ 是一對一。因為已經有 $T(\mathbf{0})=T(\mathbf{x}-\mathbf{x})=T(\mathbf{x})-T(\mathbf{x})=\mathbf{0}$ ，由 $T(\mathbf{x})=\mathbf{0}$ 可推論 $\mathbf{x}=\mathbf{0}$ ，即知 $\mathrm{ker}(T)=\{\mathbf{0}\}$ 。據此，若 $T$ 是一對一，則 $\dim\mathrm{ker}(T)=0$ ，由秩─零度定理可知 $\mathrm{rank}T=\dim\mathcal{V}$ 。
若 $T$ 同時是滿射和一對一，則 $\mathrm{rank}T=\dim\mathcal{W}=\dim\mathcal{V}$ ，稱為同構 (isomorphism)。在此情況下，逆變換 $T^{-1}$ 是唯一存在的。

矩陣

以下令 $T(\mathbf{x})=A\mathbf{x}$ ，或記為 $A:\mathbb{C}^n\to\mathbb{C}^m$ ，其中 $A$ 是一個 $m\times n$ 階矩陣， $\mathbb{C}^n$ 是定義域， $\mathbb{C}^m$ 是到達域。用矩陣語言來說，值域 $R(T)$ 即為 $A$ 的行空間 (column space)^[2]，

$C(A)=\{A\mathbf{x}\vert\mathbf{x}\in\mathbb{C}^n\}$ ，

核 $\mathrm{ker}(T)$ 即為 $A$ 的零空間 (nullspace)，

$N(A)=\{\mathbf{x}\in\mathbb{C}^n\vert A\mathbf{x}=\mathbf{0}\}$ 。

行空間 $C(A)$ 是到達域 $\mathbb{C}^m$ 的一個子空間，零空間 $N(A)$ 是定義域 $\mathbb{C}^n$ 的一個子空間。矩陣版的秩─零度定理如下：

$n=\dim N(A)+\dim C(A)$ ，

其中 $\mathrm{rank}A=\dim C(A)$ 稱為 $A$ 的秩， $\mathrm{nullity}A=\dim N(A)$ 稱為 $A$ 的零度。

類似線性變換，矩陣的子空間映射性質如下：

若 $A$ 是滿射，則 $C(A)=\mathbb{C}^m$ ，就有 $\mathrm{rank}A=m$ ，這時 $A$ 的線性獨立列向量總數等於列數 $m$ ，稱為滿列秩 (full row rank)。
若 $A$ 是一對一，則 $N(A)=\{\mathbf{0}\}$ ，秩─零度定理表明 $\mathrm{rank}A=n$ ，這時 $C(A^T)=\mathbb{C}^n$ (因為 $\dim C(A^T)=\dim C(A)=\mathrm{rank}A$ ，見“行秩=列秩”)， $A$ 的線性獨立行向量總數等於行數 $n$ ，稱為滿行秩 (full column rank)。
若 $A$ 同時是滿列秩和滿行秩，則 $\mathrm{rank}A=m=n$ ，稱為滿秩，換句話說， $A$ 是一個可逆矩陣。

用語比較

本文介紹的線性變換與矩陣的對應用語整理於下。

$T:\mathcal{V}\to\mathcal{W}$ 是一個線性變換。

值域： $R(T)=\{T(\mathbf{x})\vert\mathbf{x}\in\mathcal{V}\}\subseteq\mathcal{W}$
核： $\mathrm{ker}(T)=\{\mathbf{x}\in\mathcal{V}\vert T(\mathbf{x})=\mathbf{0}\}\subseteq\mathcal{V}$
秩： $\mathrm{rank}T=\dim R(T)$
零度： $\mathrm{nullity}T=\dim \mathrm{ker}(T)$
滿射： $R(T)=\mathcal{W}$ ，即 $\mathrm{rank}T=\dim\mathcal{W}$
一對一 (單射)： $\mathrm{ker}(T)=\{\mathbf{0}\}$ ，即 $\mathrm{rank}T=\dim\mathcal{V}$
同構： $\mathrm{rank}T=\dim\mathcal{W}=\dim\mathcal{V}$

$A$ 是一個 $m\times n$ 階矩陣，即 $A:\mathbb{C}^n\to\mathbb{C}^m$ 。

行空間： $C(A)=\{A\mathbf{x}\vert\mathbf{x}\in\mathbb{C}^n\}\subseteq\mathbb{C}^m$
零空間： $N(A)=\{\mathbf{x}\in\mathbb{C}^n\vert A\mathbf{x}=\mathbf{0}\}\subseteq\mathbb{C}^n$
秩： $\mathrm{rank}A=\dim C(A)$
零度： $\mathrm{nullity}A=\dim N(A)$
滿列秩： $C(A)=\mathbb{C}^m$ ，即 $\mathrm{rank}A=m$
滿行秩： $N(A)=\{\mathbf{0}\}$ ，即 $\mathrm{rank}A=n$
滿秩： $\mathrm{rank}A=m=n$

註解
[1] 如果向量空間 $\mathcal{V}$ 與 $\mathcal{W}$ 佈於一個體 (field) $\mathcal{F}$ ，譬如，實數系或複數系，則純量 $c\in\mathcal{F}$ 。
[2] 在台灣，橫向稱為列，縱向稱為行。在中國大陸，橫向稱為行，縱向稱為列。

8 Responses to 線性變換與矩陣的用語比較

Watt Lin says:

11/12/2012 at 4:27 pm

感謝老師詳細的闡述，幫助我建立觀念。
想請教老師，這次的主題，與傅立葉變換，有沒有關聯？
若有關聯，能否舉例說明？

- ccjou says:
  
  11/12/2012 at 6:25 pm
  
  傅立葉轉換可以當作本文的例子。傅立葉轉換是定義於無窮維空間的線性變換，離散傅立葉轉換則是定義於有限維空間 (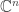 $\mathbb{C}^n$ ) 的線性變換，因此離散傅立葉轉換可表示成矩陣運算形式，變換矩陣稱為傅立葉矩陣。
  
  離散傅立葉轉換
  
  現實上，我們採用離散傅立葉轉換的原因在於電腦僅能處理有限維的矩陣運算。
  
  - Watt Lin says:
    
    11/12/2012 at 7:25 pm
    
    感謝老師的回答。
    
tsao says:

07/10/2019 at 5:25 pm

老師在矩陣的子空間映射性質中第一點:
若 A 是滿射，則 C(A)={C}^m，就有 {rank}A=m，這時 A 的線性獨立列向量總數等於列數 m，稱為滿列秩 (full row rank)。
這邊是否打錯了，我的理解應該是A的線性獨立行向量總數等於列數 m才對。
如果我的理解不對請老師糾正~

- CunZhang says:
  
  07/02/2021 at 9:01 pm
  
  這邊周老師打的沒錯呀，滿射（onto）表示T(v)這個值一定找到v是的映射成立，也就是對於Ax=b而言，任意b都能找到解，A是mxn那麼C(A)就會佈滿整個F^m空間，此時rank(A)=r=m叫full row rank。你的理解也沒錯，A的秩可以是獨立行向量個數同時也是獨立列向量個數，還記得做高斯消去法的時候，pivot對應到的行數與列數都一樣嗎。
  
Marvin Fan says:

07/07/2021 at 5:53 pm

老師您好，請教一下，以下這段是不是有筆誤？

行空間 C(A) 是定義域 \mathbb{C}^m 的一個子空間，零空間 N(A) 是到達域 \mathbb{C}^n 的一個子空間。

行空間是不是應該是到達域的一個子空間，零空間是定義域的一個子空間才對？
總覺得這樣好像合理些。

- zachary says:
  
  06/12/2023 at 7:23 am
  
  我也是覺得這段有筆誤
  
  - ccjou says:
    
    06/12/2023 at 10:24 pm
    
    已訂正, 謝謝。

	jianglong on Strassen 演算法──分治矩陣乘法
	jianglong on Strassen 演算法──分治矩陣乘法
	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明