本文的閱讀等級:中級
矩陣的對角化 (diagonalization) 是特徵分析在簡化矩陣運算上的一個重要應用 (見“矩陣函數 (上)”)。令 為一個
階矩陣。若存在一個
階可逆矩陣
使得
,其中
是對角矩陣,則稱
是可對角化矩陣 (diagonalizable matrix),且
是
的對角化矩陣 (diagonalizing matrix)。如果不存在滿足上述條件的
,則稱
是不可對角化矩陣。本文介紹可對角化矩陣的判定方法,通過探討此主題讀者可以深入理解矩陣特徵分析的概念與操作。
我們從矩陣特徵分析開始。令 為
的一個特徵值,對應的特徵向量
滿足特徵方程
。注意,雖然
滿足上式,但為了使事情有趣,我們不允許特徵向量為零向量。將特徵方程改寫為
,其中
是單位矩陣,由此展開一連串關於特徵值和特徵向量性質與計算方法的推理:
-
對於特徵值
,
的零空間 (nullspace) 必定包含非零向量 (否則便不存在非零特徵向量),以
表示,說明
是一個不可逆矩陣。行列式給出一個簡單的檢查公式
,於是我們定義
階方陣
的特徵多項式 (characteristic polynomial) 為
,
特徵值
即為
的根。將此
階行列式展開,可確認
為
次多項式。根據代數基本定理,
次多項式
恰有
個根,也就是說,包含重根在內,
有
個特徵值。
- 針對一個特徵值
,不論是單根或重根,對應的特徵向量必屬於
,我們稱它為對應
的特徵空間 (eigenspace)。所以,特徵向量與特徵空間彼此關係的精確描述是:特徵空間中的非零向量都是特徵向量。
令 為
階矩陣
的一個特徵值 (包含相重特徵值),對應的特徵向量為
,
。寫出
個特徵方程,
。
將上面的方程組合併為矩陣形式,如下:
設 階特徵向量矩陣
,且
為特徵值構成的對角矩陣。特徵方程的矩陣表達式即為
。若
有
個線性獨立的特徵向量,則
是可逆的,
可分解為
,或者說
對角化
,
;反之,如果
不擁有
個完整的線性獨立的特徵向量,則
是不可逆的,故無法對角化
。從
的特徵值是否足以判定它具有完整的線性獨立特徵向量呢?這個問題僅存在部分答案,下面分開兩種情況討論:(1)
的特徵值兩兩相異,(2)
有相重的特徵值。
定理 1. 若 的特徵值兩兩相異,則
有完整的線性獨立特徵向量。
我們用歸納法證明此定理 (其他證法請見“相異特徵值對應線性獨立的特徵向量之簡易證明”)。對於 ,
,考慮線性組合式
。
上式通乘 ,並代入特徵方程:
。
上式減去線性組合式與 的乘積,可得
。
因為 且
,推知
。將前述步驟的乘數
替換為
,以同樣方法可證得
。這說明了對應兩相異特徵值的兩個特徵向量必為線性獨立的。接下來,對於相異
,假設
,考慮包含三個向量的線性組合式
。
重複前述推導步驟,將上式通乘 並代入特徵方程,化簡可得
。
上式減去線性組合式與 的乘積,如下:
。
利用前述結果,對應兩相異特徵值的特徵向量是線性獨立的,推論 。又因
兩兩相異, 可知
。重複同樣過程也可以證明
,因此
,
和
是線性獨立。推廣至
個相異特徵值,你可以歸納出所有
個特徵向量形成一個線性獨立集。
第二種情況比較複雜,當 有相重特徵值時,
可能是可對角化的,也可能是不可對角化的。見下例,考慮
。
三角矩陣的特徵值即為其主對角元,所以 和
的特徵值同為
。對於
,
有特徵向量
,對於
,
有兩個獨立的特徵向量
和
,所以
是可對角化的,如下:
。
對於 ,
有特徵向量
,對於
,
僅有一個特徵向量
,
,總計
只有兩個獨立特徵向量,因此不存在可逆對角化矩陣
,
是不可對角化的。
上面這個例子很自然地引伸出一些有用的概念。對於 階方陣,特徵值
為特徵多項式
的根,我們稱重根數為代數重數 (algebraic multiplicity)。對應特徵值
的特徵空間維數,
,亦即所能找到最大線性獨立向量個數,則稱為
的幾何重數 (geometric multiplicity)。代數重數和幾何重數有兩個極具意義的性質:(1) 因為特徵多項式
共有
個根,所有相異特徵值的代數重數之和也等於
;(2) 對於任一特徵值
,幾何重數必定不大於其代數重數。由於證明較為冗長,我們留待本文最末再詳細解說。如果某一個特徵值的幾何重數小於其代數重數,我們稱此方陣為缺陷 (defective) 矩陣。上例中,
不是缺陷矩陣,但
是缺陷矩陣。
定理 2. 方陣 是可對角化的一個充要條件為對於每一個特徵值
,代數重數等於幾何重數,換句話說,不可對角化矩陣同義於缺陷矩陣。
證明於下。假設 階方陣
是可對角化的,則
有
個線性獨立的特徵向量。設特徵值
的代數重數為
,一定存在可逆矩陣
可將
對角化為
,
且 不為
階對角矩陣
的特徵值,故
是可逆矩陣。考慮
。
因為可逆矩陣乘法不改變矩陣秩,就有
。
利用秩—零度定理,
。
特徵值 的幾何重數
確實等於代數重數
。再來證明相反方向陳述。假設
階方陣
有
個相異特徵值
,
,其幾何重數都等於代數重數,以
表示。顯然,特徵向量總數為
,剩下來只要證明所有這
個特徵向量是線性獨立的。主要的理由有二:(1) 對應特徵值
的
個特徵向量是線性獨立的,因為這
個特徵向量為特徵空間
的基底向量;(2) 對應兩相異特徵值
的特徵空間不交集,
,這指出對應
的特徵向量 (屬於
) 和對應
的特徵向量 (屬於
) 是線性獨立的。所以
有完整的
個線性獨立特徵向量。
最後補充說明對於每一個特徵值 ,它的幾何重數必不大於代數重數。例如,
階方陣
有兩組重數為
的特徵值
,不可能發生以下狀況:
,而
,亦即有一個獨立特徵向量對應特徵值
,但有三個獨立特徵向量對應特徵值
。基礎線性代數教科書常視此性質為理所當然,下面提供一個嚴格的證明[1]。設
階方陣
的特徵值
其幾何重數為
,亦即特徵空間
包含
個線性獨立向量
滿足
,
。將此向量集擴充為
(或
) 的一組基底
(詳細演算法請見“每週問題 April 26, 2010”),並建立可逆矩陣
。計算
上式中 。令
。
方陣 相似於
,兩矩陣有相同的特徵多項式 (見“相似變換下的不變性質”)。方陣
的特徵多項式為
分塊上三角矩陣的行列式為主對角分塊行列式的乘積 (參閱“利用分塊矩陣證明 det(AB)=(det A)(det B)”),所以
上式指出 的特徵多項式有至少
次重根
,故
的幾何重數必不大於代數重數。(另一個採用 Schur 定理的證明見“幾何重數不大於代數重數的證明”,或直接用定義來證明,見“特徵值的代數重數與幾何重數”。)
參考來源:
[1] Thomas S. Shores, Applied Linear Algebra and Matrix Analysis, 2007.

周老师,您好,有几个问题确实想不明白了,向您请教一下,其中第一和第二个问题,我想到了答案,但不知对否?剩下的两个就全然不知该怎么弄了。
1、如何手工构造一个非缺陷矩阵A,要求A具有n个相异特征值?只要找一组基S,再指定n个彼此不同的特征值组成一个对角阵W,S*W*(S逆)即为所求的非缺陷矩阵A。
2、如何手工构造一个非缺陷矩阵A,要求A的某个特征值的代数重数是3,且它对应的特征空间的维数也是3?这个也比较容易,在问题1的基础上,只要把某个特征值重复3次就可以了。
3、如何构造一个缺陷矩阵B,要求B的某个特征值的代数重数是4,但它所对应特征空间的维数只有2?
4、我知道,矩阵分病态矩阵和良态矩阵,但不是绝对的只有两类,就像音量从大到小是连续的一样,矩阵的态性从良态到病态通过“条件数”这个参数也可以连续变化。不恰当地类推一下,缺陷矩阵和非缺陷矩阵之间是否也可以连续过渡?
怎么过渡?
問題1,2可藉由對角化解決,這是對的。
問題3,4涉及Jordan form,我再另文解說。這裡先簡單回答。問題3,下為二例, ,
, 。
。
問題4,缺陷矩陣和非缺陷矩陣不存在連續過渡,因為特徵空間維數(即幾何重數)並非矩陣各元的連續函數。例如,若 ,
, 僅有一個特徵向量
僅有一個特徵向量  。當
。當  ,
, 的特徵向量為
的特徵向量為  和
和  。
。
非常感谢周老师如此神速的解答!
关于第3个问题,是跟Jordan块的个数有关?
关于第4个问题,我没有说清楚,我真正想说的是,类似连续的那种效果,可能说离散更贴切些,比如修改对角阵上的某个数,那么第1个问题里面的矩阵即可变成第2个问题里面的矩阵,接着再怎么修改一个数或者少数几个数可以变成第三个问题里面的病态矩阵呢?这种该法是否存在?
問題3,Jordan 分塊數即為幾何重數,見下文:
問題4,當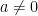 ,則
,則 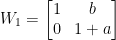 ,
, 屬於第1個問題的矩陣。若
屬於第1個問題的矩陣。若  ,則
,則 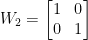 ,此時
,此時  屬於第2個問題的矩陣。若
屬於第2個問題的矩陣。若 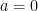 但
但  ,則
,則  ,
, 屬於第3個問題的矩陣。
屬於第3個問題的矩陣。
上述現象的理論是 並非
並非  的連續函數,請見下文最末一段:
的連續函數,請見下文最末一段:
如果仍有疑問,可以再提出來討論。
老师您好,我认为 要证明不同特征值的特征向量放在一起得到的n个向量仍然相互独立,仅仅论证“任意两个特征子空间之间无交集”从逻辑上是不够的。顺着这个逻辑需要证明的,应该是,任何一个特征子空间和“其他所有特征子空间的并集”无交集