本文的閱讀等級:中級
考慮一有限維內積空間 ,且
。任意
的內積記為
。令
為
的一組基底。向量空間
中任一向量
可唯一表示成
的線性組合:
。
收集所有係數 即構成向量
參考基底
的座標向量
,兩者之間具有一對一的映射關係:
,
我們稱 所屬的向量空間
與
所屬的幾何向量空間
是同構的 (isomorphic,見“同構的向量空間”)。欲得到
的座標向量
必須解開一
階線性方程組,這不是我們樂見的事。但如果
是一組單範正交基底 (orthonormal basis),也就是說
若
,
若
,則完全不需要經過解方程式過程即可求得
。利用內積的半雙線性性質 (見“內積的定義”),可得
故 有下列正交分解展開式:
,
其中 即為
至「直線」
的正交投影分量。見下例,
中任意兩向量
和
的內積定義為
。考慮單範正交基底
,其中
。
給定 ,其座標向量為
,正交分解式如下:
。

Joseph Fourier (1768-1830) From http://www-history.mcs.st-and.ac.uk/BigPictures/Fourier.jpeg
公元1822年,法國數學家、物理學家傅立葉 (Joseph Fourier) 將他在熱傳的研究成果出版成書 Théorie analytique de la chaleur (英譯 The analytic theory of heat),其中最重大的數學貢獻是他提出了一個獨特的正交分解展開式[1]。傅立葉考慮單變量週期函數形成的向量空間,並以無限多個餘弦和正弦函數構成單範正交集,因此設計出無窮級數形式的展開式,後人稱為傅立葉級數 (Fourier series)[2]。傅立葉宣稱任何週期函數──不論連續與否──皆可用傅立葉級數表示。這個結果並不正確,德國數學家狄利克雷 (Johann Peter Gustav Lejeune Dirichlet) 率先給出一週期函數 可展開成傅立葉級數的條件[3]:
- 此函數必須是有界的 (bounded),即對於任意
,
,
是一正實數;
- 在任意區間內,除了有限個不連續點,
必須是連續函數;
- 在任意區間內,
必須僅包含有限個極值;
- 在一週期內,
的積分必須收斂。
儘管適用性限定於滿足 Dirichlet 條件的函數,傅立葉級數現今已然是應用數學的基本工具,在訊號處理、影像處理、計量經濟、震動分析、聲學、光學等領域都有廣泛的應用。下面我們介紹線性代數觀點下的傅立葉級數。
傅立葉的研究對象是單變量週期函數 ,設週期為
(稍後我們會解除這個限制)。對於任意整數
,
,因此僅須考慮一週期內的
。令
是由定義於區間
(亦可選擇
) 的實函數所成的內積空間,請注意,函數空間
是一無限維空間 (見“從幾何向量空間到函數空間”)。對於
中兩實函數
和
,其內積定義如下 (有些學者採用不含
的內積定義,如此一來,
則乘入餘弦和正弦函數):
,
則 的「長度」或範數 (norm) 為
。
既然傅立葉面對的是週期函數,不難想像他會設法將 中任一函數分解為吾人熟悉的週期函數的線性組合,而非多項式 (如“Legendre 多項式”) 的線性組合。我們知道傅立葉最終選擇了餘弦和正弦函數,可能原因有二:第一,餘弦和正弦函數有非常簡單的微分與積分公式;第二點尤其重要,餘弦和正弦函數可建構出單範正交集。但為什麼傅立葉要同時使用餘弦和正弦函數?因為餘弦是偶函數,
,正弦是奇函數,
,而任何函數
都可分解成偶函數與奇函數的和:
。
考慮無窮函數集合
,
但請注意我們不確知 是否為無限維空間
的一組基底。令
和
為非負整數。運用積化和差公式[4]可算得
且
因此確定 中所有函數的「長度」都等於1,任兩相異函數彼此正交,故
是一個單範正交集。令
代表
的領先
個函數所成的集合,明顯地,
也是一個單範正交集。令
代表單範正交集
擴張成的子空間,
是無限維向量空間
的一個子空間,且
。對於任一
,
至子空間
的正交投影可由各個投影分量組成:
,
其中 和
稱為傅立葉係數,分別如下:
我們令 首項為
使得
計算公式同時適用
和
。在子空間
中,就給出的內積定義而言,正交投影
是
的最小平方近似 (見“正交補餘與投影定理”)。令
,無窮級數
即為
的傅立葉級數。無限維向量空間與一般有限維向量空間的主要不同之處在於我們未能認定傅立葉挑選的單範正交集
的確是
的一組基底,也因此不能保證每一
都有
。事實上,若
是一個非週期函數,則
根本不可能等於
,因為
是週期函數的線性組合。縱使
是一個週期函數並滿足 Dirichlet 條件,亦不能保證
逐點收斂至
,只能夠說「整個傅立葉級數
收斂至
」,嚴謹的數學陳述是
。譬如,若
在
不連續,但左右可微分,可以證明
收斂至
,其中
,
。
下面我們用一個例子來說明。考慮週期等於 的方波:
在 ,
的值未定義。縱使我們不知道
仍可計算傅立葉係數,結果如下:
,
,且
若
是偶數,
若
是奇數,於是得到
的傅立葉級數:
。
除了 ,對於每一
,都有
。當
,
。下圖顯示隨著
增大,
逼近方波
的情況 (設
,此圖區間即為
)。

Fourier Series: Square Wave From http://mathworld.wolfram.com/images/eps-gif/FourierSeriesSquareWave_800.gif
下文將繼續探討如何推廣傅立葉級數於任意週期的情況,推導傅立葉級數的指數表達式,並說明傅立葉係數與其所描述的函數之間的關係。
參考文獻:
[1] 維基百科:傅立葉
[2] 維基百科:傅立葉級數
[3] 維基百科:Dirichlet conditions
[4] 維基百科:積化和差公式

當傅立葉級數的首項寫成 時,
時, 已不再是標準(單範)正交集。
已不再是標準(單範)正交集。
沒錯,若要維持 是標準正交集,則傅立葉級數應寫成
是標準正交集,則傅立葉級數應寫成

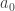 則應改為
則應改為

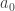 積分式中的
積分式中的 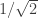 提出來,傅立葉級數的首項因此變成
提出來,傅立葉級數的首項因此變成  。
。
而
這麼寫大概會讓很多人頭疼。絕大多數的教科書都將
在工程領域中,多數人不是從線性代數認識傅立葉級數(或分析),而是從訊號處理課程學會的。或許編寫教科書的人也不認為傅立葉分析的線性代數觀點有多麼重要吧。
我將原文的f(t)全改為f(x),以便保留f(t)給定義於區間[0,T]的週期函數。
請問老師
我是工科學生,從學習傅立葉分析到快速傅立葉轉換必須要具備哪些基礎?
剛接觸傅立葉級數到傅立葉轉換,本來以為這樣就夠了。但是看了老師的文章,才發現缺少了很多觀念(如正交、函數內積)。工程數學課本內容都簡單帶過…想了解的更透徹一點(如:複數平面為什麼可以用類似向量方式去計算?)
希望出社會前的短短幾年,可以把這個大空缺補上。
感謝老師!
線性代數的內積空間是最重要的基礎。你可以依序閱讀「傅立葉分析專題」文章,如果碰到不清楚的概念或方法,此即需要進一歩補強的地方,這時可以從「閱讀導引」查找相關的討論文章。我建議你不必急著解答心裡的疑問,不妨如讀小說一般大量地閱讀本站文章,過一陣子答案自然會揭示開來。
好的。
請問傅立葉轉換和內積空間的物理意義為何?
內積空間是數學概念和理論,本身沒有什麼物理意義。傅立葉轉換如果應用於信號處理,即是將時域表達的信號轉換為頻域表示,根據它在各頻率的分配比較容易分析處理。這裡面的內容含蓋一大部分的電機領域,很難三言兩語道盡。
謝謝您的解說,讓我了解原來物理意義指的是信號轉換。這兩者我已經讀過信號與系統與線性代數,個別的定義與應用略有了解,不過請問您這兩者間有沒有關聯?謝謝您。
既然你這麼問就表示你們的「信號與系統」沒有採用線性代數符號或觀點來解釋。事實上,只要是線性系統就必定與線性代數有關,你學過的所有變換,Fourier transform,Laplace transform,z-transform全部都是定義在無限維空間上的線性變換。
難怪我會有這個疑惑,原來是我的課本沒有採用線性代數的符號或觀點解釋,謝謝您。相信我把您的網站裡的資料讀熟後會更加了解。
「信號與系統」沒有採用線性代數符號或觀點來解釋。
這句話,我想到以下:
教科書的編寫,若有考慮學生要學習很多科目,適當引入某些符號,而且符號統一,學生的學習,會比較順利。
或許一個學期能教的課程有限,時間不夠,老師把自己份內的課講完,已經很不容易,無暇顧及學生在以往聽過哪些課程。
如果有老師,擅長啟發思考,讓學生把所學的多項科目,作系統式連結,學生的頭腦裡,會得到清晰的觀念。
這在課程上,幾乎很難完成。
學生可能在學期結束後,沒有考試壓力,才有時間去深思。
甚至,畢業後的好幾年,漸漸得到領悟。
我經常到《線代啟示錄》網站,得到不少重要觀念的澄清,很感謝老師您的啟發。
你講出了高等教育(或公司組織)長久以來的一個問題:刻意無視(wilful blindness),人們不願意說出真相,也不想認清真相。
目前的高等教育分科很細,每一門科目交由一位老師專門講授,這種方式對老師們來說可謂輕鬆愉快。另一方面,教科書的編寫者也希望他的課本需要的預備知識越少越好,最好只有加減乘除,這樣容易取得市場佔有率,同時也不會阻撓基礎科目沒學好的學生前進。拿「信號與系統」來說,多數課本不會高調地討論內積空間和線性變換(頂多偶爾使用幾個矩陣乘法運算),它們假裝信號是信號,向量是向量,兩者無關。所以學生們知道如何計算各種轉換,甚至設計濾波器,但他們(多數)不曉得原來這些變換是同構的,也就是將某一個向量空間的向量(信號)以一對一的方式映射至另一個向量空間的向量(變換)。如你說的,等到他們畢業多年後,某一天(不知甚麼原因)才突然領悟原來當初所學的東西竟然同源同種。這就是我自己的親身經歷。
請看這個關於刻意無視的影片:
「刻意無視」的影片,講出很重要的觀念。
另外,我想補充發表一些看法。
民國73年,我進入高中,當年國立編譯館推出各科新教材。
國文、英文、歷史、地理、數學、物理、化學,皆用新版本。
高一的課程,我適應良好。
高二及高三期間,發現物理課本,
好像由不同小組的專家編寫,小組的溝通討論,可能忽略某些細節。
光學的部分歸光學,似乎不必講求某些符號的習慣,儘量與力學的習慣相似。
數學教材有的方法、符號,例如三維向量: i, j, k 單位向量,
在物理課本卻沒看到,等老師補充,我才敢把數學課本的符號,用於物理。
微分、積分,新教材數學課本已經有,物理課本卻避開微積分符號。
我高中畢業時,大學沒考好,去補習一年,
自己買大學物理學教材,又向學長借舊版的國立編譯館物理課本,
總共對照三個物理學版本,自己建立一些比較清晰的觀念。
在網頁看到:「信號與系統」沒有採用線性代數符號或觀點來解釋。
我聯想許多事,整個科學教育,
有沒有人提倡:
由小學、國中、高中、大學,重新檢視教材編排模式,
未來的教材,要使學習連貫,而且講究符號一致。
這可能是件浩大工程,如果有人提倡,也許未來能夠實現。
可能是我讀的課本比較舊的關係吧,Signals and Systems (2nd Edition)Alan V. Oppenheim (Author), Alan S. Willsky (Author), with S. Hamid (Author),1996年出版的出了書。
我將你的兩個迴響合併在一起,讀起來還是怪怪的。這是我很久以前教「信號與系統」時的課本:Signals, Systems, and Transforms [Leland B. Jackson] , 1991年。有一次我問一位同事(她是信號處理的專家,也在本校教線性代數),為甚麼數位信號處理的教科書(幾乎)都不使用矩陣和向量?她也沒有答案。
請問 “任何函數 f(x) 都可分解成偶函數與奇函數的和:”的下一個式子, 有點看不懂, 因為等號左邊是f(x), 但是等號右邊加完後卻是2f(x)??! Thank you. -Chun-Yao
你的螢幕顯示可能出問題,請刷新頁面再看一次公式是