利用行列式計算多邊形面積

本文的閱讀等級：初級

考慮平面上的一個 $n$ 邊形，令 $(x_0,y_0),(x_1,y_1),\ldots,(x_{n-1},y_{n-1})$ 表示逆時針方向排序的 $n$ 個端點座標 (參見下圖)。這個 $n$ 邊形面積記為 $a$ ，可由 $n$ 個二階行列式之和算出：

$\displaystyle a=\frac{1}{2}\left(\begin{vmatrix} x_0&x_1\\ y_0&y_1 \end{vmatrix}+\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}+\cdots+\begin{vmatrix} x_{n-2}&x_{n-1}\\ y_{n-2}&y_{n-1} \end{vmatrix}+\begin{vmatrix} x_{n-1}&x_0\\ y_{n-1}&y_0 \end{vmatrix}\right)$ ，

稱為測量員 (surveyor) 公式。有人將此公式簡明地表示為^[1]：

$\displaystyle a=\frac{1}{2}\begin{vmatrix} x_0&x_1&x_2&\cdots&x_{n-2}&x_{n-1}&x_0\\ y_0&y_1&y_2&\cdots&y_{n-2}&y_{n-1}&y_0 \end{vmatrix}$ 。

測量員公式的計算方式形如

$\begin{matrix} x_0 & ~ & x_1 & ~ & x_2 & \cdots & x_{n-1} & & x_{0} \\ ~ & \times & & \times & & & & \times & ~ \\ y_0 & ~ & y_1 & ~ & y_2 & \cdots & y_{n-1} & & y_{0} \end{matrix}$

所以又稱為鞋帶 (shoelace) 公式。我們知道二階行列式 $\det A$ 等於 $A$ 的兩個列向量 (row vector) 所張開的平行四邊形的有號面積 (見“行列式的運算公式與性質”)。等式 $\det A^T=\det A$ 說明列向量張開的平行四邊形有號面積等於行向量 (column vector) 張開的平行四邊形有號面積。根據右手定則，若右手拇指外的四根手指的彎曲方向 (即逆時針方向) 視為由第一列向量至第二列向量的旋轉方向，則面積為正，反之，面積為負。下面我們利用行列式的幾何意義與基本性質證明測量員公式。

首先推導三角形面積公式。若 $n=3$ ，令三角形的兩個邊向量為

$\mathbf{u}=\begin{bmatrix} x_1-x_0\\ y_1-y_0 \end{bmatrix},~\mathbf{v}=\begin{bmatrix} x_2-x_0\\ y_2-y_0 \end{bmatrix}$ 。

向量 $\mathbf{u}$ 和 $\mathbf{v}$ 所張的平行四邊形面積為

$\displaystyle \det\begin{bmatrix} \mathbf{u}&\mathbf{v} \end{bmatrix}=\begin{vmatrix} x_1-x_0&x_2-x_0\\ y_1-y_0&y_2-y_0 \end{vmatrix}$ ，

可知端點為 $(x_0,y_0), (x_1,y_1), (x_2,y_2)$ 的三角形面積等於

$\displaystyle a=\frac{1}{2}\begin{vmatrix} x_1-x_0&x_2-x_0\\ y_1-y_0&y_2-y_0 \end{vmatrix}$ 。

利用行列式基本性質：(1) 行列式對於任一行都是線性函數，(2) 交換兩行改變正負號，(3) 兩行相同則行列式為零，可得

$\begin{aligned} \begin{vmatrix} x_1-x_0&x_2-x_0\\ y_1-y_0&y_2-y_0 \end{vmatrix}&=\begin{vmatrix} x_1&x_2-x_0\\ y_1&y_2-y_0 \end{vmatrix}+\begin{vmatrix} -x_0&x_2-x_0\\ -y_0&y_2-y_0 \end{vmatrix}\\ &=\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}+\begin{vmatrix} x_1&-x_0\\ y_1&-y_0 \end{vmatrix}+\begin{vmatrix} -x_0&x_2\\ -y_0&y_2 \end{vmatrix}+\begin{vmatrix} -x_0&-x_0\\ -y_0&-y_0 \end{vmatrix}\\ &=\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}-\begin{vmatrix} x_1&x_0\\ y_1&y_0 \end{vmatrix}-\begin{vmatrix} x_0&x_2\\ y_0&y_2 \end{vmatrix}+\begin{vmatrix} x_0&x_0\\ y_0&y_0 \end{vmatrix}\\ &=\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}+\begin{vmatrix} x_0&x_1\\ y_0&y_1 \end{vmatrix}+\begin{vmatrix} x_2&x_0\\ y_2&y_0 \end{vmatrix},\end{aligned}$

故三角形面積為^[2]

$\displaystyle a=\frac{1}{2}\left(\begin{vmatrix} x_0&x_1\\ y_0&y_1 \end{vmatrix}+\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}+\begin{vmatrix} x_2&x_0\\ y_2&y_0 \end{vmatrix}\right)$ 。

請你自行舉些例子驗證這個公式。

接著考慮 $n$ 邊形， $n>3$ 。為了使用三角形面積公式，將 $n$ 邊形切割成 $n-2$ 個三角形。我們看 $n=5$ 的情況。見下圖，五邊形被分割成 3 個三角形，按逆時針方向端點標號，分別表示為 $\triangle(0,1,2),\triangle(2,3,4),\triangle(4,0,2)$ 。

五邊形切割成3個三角形

五邊形面積等於3個三角形面積之和，即

$\displaystyle \begin{aligned} a&=\frac{1}{2}\left(\begin{vmatrix} x_0&x_1\\ y_0&y_1 \end{vmatrix}+\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}+\begin{vmatrix} x_2&x_0\\ y_2&y_0 \end{vmatrix}\right)\\ &+\frac{1}{2}\left(\begin{vmatrix} x_2&x_3\\ y_2&y_3 \end{vmatrix}+\begin{vmatrix} x_3&x_4\\ y_3&y_4 \end{vmatrix}+\begin{vmatrix} x_4&x_2\\ y_4&y_2 \end{vmatrix}\right)\\ &+\frac{1}{2}\left(\begin{vmatrix} x_4&x_0\\ y_4&y_0 \end{vmatrix}+\begin{vmatrix} x_0&x_2\\ y_0&y_2 \end{vmatrix}+\begin{vmatrix} x_2&x_4\\ y_2&y_4 \end{vmatrix}\right),\end{aligned}$

其中三角形 $\triangle(4,0,2)$ 分別與 $\triangle(0,1,2)$ 和 $\triangle(2,3,4)$ 擁有共邊 $(0,2)$ 和 $(2,4)$ 。在計算相鄰三角形面積時，因為共邊兩端點的排序相反，就有 $\begin{vmatrix} x_0&x_2\\ y_0&y_2 \end{vmatrix}+\begin{vmatrix} x_2&x_0\\ y_2&y_0 \end{vmatrix}=0$ 和 $\begin{vmatrix} x_2&x_4\\ y_2&y_4 \end{vmatrix}+\begin{vmatrix} x_4&x_2\\ y_4&y_2 \end{vmatrix}=0$ ，故五邊形面積公式為

$\displaystyle a=\frac{1}{2}\left(\begin{vmatrix} x_0&x_1\\ y_0&y_1 \end{vmatrix}+\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}+\begin{vmatrix} x_2&x_3\\ y_2&y_3 \end{vmatrix}+\begin{vmatrix} x_3&x_4\\ y_3&y_4 \end{vmatrix}+\begin{vmatrix} x_4&x_0\\ y_4&y_0 \end{vmatrix}\right)$ 。

運用同樣方法可歸納證明一般多邊形的測量員面積公式。

註解
[1] 行列式僅定義於方陣，何不也定義非方陣的行列式？譬如，根據測量員公式，為何不將 $2\times 3$ 階矩陣的行列式定義為

$\begin{vmatrix} x_0&x_1&x_2\\ y_0&y_1&y_2 \end{vmatrix}=\begin{vmatrix} x_0&x_1\\ y_0&y_1 \end{vmatrix}+\begin{vmatrix} x_1&x_2\\ y_1&y_2 \end{vmatrix}+\begin{vmatrix} x_2&x_0\\ y_2&y_0 \end{vmatrix}$ ？

我們可以任意定義 $2\times 3$ 階矩陣的函數，但不能稱之為行列式。對於一個 $m\times n$ 階矩陣 $A$ ，假設函數 $d(A)$ 傳回一純量。若 $m=n$ ，則 $d(A)=\det(A)$ 。我們要求函數 $d$ 必須滿足行列式的基本性質，譬如，行列式可乘公式： $\det(AB)=(\det A)(\det B)$ ，其中 $A$ 和 $B$ 是同階方陣。具體地說，若 $A$ 是 $m\times n$ 階矩陣且 $B$ 是 $n\times p$ 階矩陣，則 $d(AB)=d(A)d(B)$ 。設 $A=\begin{bmatrix} 1&0\\ 0&1\\ 0&0 \end{bmatrix}$ ，則 $AA^T=\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&0 \end{bmatrix}$ 且 $A^TA=\begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}$ 。然而，

$\begin{aligned} 1&=\begin{vmatrix} 1&0\\ 0&1 \end{vmatrix}=\det(A^TA)=d(A^TA)=d(A^T)d(A)\\ &=d(A)d(A^T)=d(AA^T)=\det(AA^T)=\begin{vmatrix} 1&0&0\\ 0&1&0\\ 0&0&0 \end{vmatrix}=0. \end{aligned}$

這個矛盾說明非方陣不存在具有與行列式相同性質的函數。

[2] 利用餘因子 (cofactor) 展開，三角形面積亦可表示為

$\displaystyle a=\frac{1}{2}\begin{vmatrix} x_0&x_1&x_2\\ y_0&y_1&y_2\\ 1&1&1 \end{vmatrix}=\frac{1}{2}\begin{vmatrix} 1&1&1\\ x_0&x_1&x_2\\ y_0&y_1&y_2 \end{vmatrix}$ 。

5 Responses to 利用行列式計算多邊形面積

馬鑑一 says:

10/07/2014 at 11:46 am

用三階行列式推導鞋帶公式
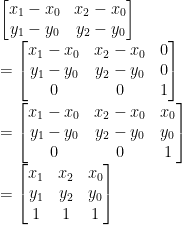
$\begin{bmatrix} x_1-x_0&x_2-x_0\\ y_1-y_0&y_2-y_0\\ \end{bmatrix}\\ = \begin{bmatrix} x_1-x_0&x_2-x_0&0\\ y_1-y_0&y_2-y_0&0 \\ 0&0&1\\ \end{bmatrix}\\ = \begin{bmatrix} x_1-x_0&x_2-x_0&x_0\\ y_1-y_0&y_2-y_0&y_0 \\ 0&0&1\\ \end{bmatrix}\\ = \begin{bmatrix} x_1&x_2&x_0\\ y_1&y_2&y_0 \\ 1&1&1\\ \end{bmatrix}$

- ccjou says:
  
  10/07/2014 at 12:17 pm
  
  謝謝補充。
  
ianre657 says:

12/06/2014 at 3:47 pm

看這篇文章發現一個小錯誤
一開始推導三角形面積的
det[u v]=[ ]
左下角應該是y1-y0

- ccjou says:
  
  12/06/2014 at 11:28 pm
  
  謝謝指出錯誤，已更正。
  
Yu Xue says:

09/02/2019 at 4:59 am

很有意思，这个surveyor公式其实可以用微积分中的Green’s theorem来证明。（那天复习微积分看到的）。

	陳倍恩 on 線性代數的第一堂課──矩陣乘法的定義
	輕鬆談如何教學二項式定理？… on 牛頓的二項式定理 (上)
	madhouse on 高斯消去法
	WishMobile on 翻轉 LU 分解
	周子傑 on Karush-Kuhn-Tucker (KKT) 條件
	Cloud Huang on 線性泛函與伴隨