本文的閱讀等級:初級
令 和
為
階矩陣。矩陣乘積
的行列式定理說:
的行列式等於
的行列式與
的行列式之積,即
。
下面我們僅考慮 和
皆為可逆矩陣的情況。若
或
是不可逆的,則
也是不可逆的,就有
。
一般教科書裡採用的「典型」證明先引入三種基本矩陣 的行列式 (見“特殊矩陣 (10):基本矩陣”),並以矩陣乘積
表示基本列運算執行後的結果,詳述於下:
- 取代:基本矩陣
將矩陣
第
列取代為非零常數
和第
列的乘積,此運算不改變行列式,故
。
- 交換:基本矩陣
將
的第
列與第
列交換位置,這使得行列式改變符號,故
。
- 伸縮:基本矩陣
將
的第
列通乘非零常數
,行列式變為
倍,故
。
以上每一個基本列運算步驟產生 ,並滿足
。
接下來只要將矩陣 分解為基本矩陣乘積,
,然後重複使用上述關係便可歸納證出原命題:
上述證法可以簡述如下:利用高斯─約當法 (見“高斯-約當法”) 以基本列運算將分塊矩陣 化約為
,左邊分塊
的行列式乘以因子
(因為
),右邊分塊
的行列式同樣也乘以因子
,推得
。
下面我介紹一個採用分塊矩陣的「非典型」證明方法,主要的想法是以分塊矩陣乘法聯繫矩陣乘積 。首先我們要知道這個性質:分塊三角矩陣的行列式等於其主對角分塊行列式的乘積,即
,
其中 代表行列式運算,
與
是分塊方陣 (但尺寸可以不同)。上述性質來自行列式的一個運算公式,稱為餘因子公式 (或稱 Laplace 展開公式,見“行列式的運算公式與性質”)。使用數學歸納法證明。考慮
階
,其中
是
階。用第一行展開:
其中 表示刪除
的第
列與第
行而得的子陣,第 1 與 5 個等號來自餘因子公式,第 3 個等號係應用歸納假設於
階分塊子陣。
現在我們可以開始證明,這個證明的過程很類似「填字遊戲」和「數獨」,一邊猜測再一邊確認。考慮分塊三角矩陣 ,其中各分塊皆為
階方陣。對此分塊矩陣執行取代運算以消去分塊
,可得
。
注意,乘積 很巧妙地被引出來。取代運算不改變行列式,故
。
利用前述分塊三角矩陣的行列式性質,等號左邊為
。
再對等號右邊矩陣執行 次行交換以產生分塊三角矩陣,但每次交換行改變行列式的正負號,所以
。
最後將負號提出來,因為 是
階方陣,就有
,將此結果代回上式即得證。

我有一些疑問
您用分塊矩陣和取代運算證明
det |B I|=|B I|
|0 A| |-AB 0|
但是以取代運算來說
0應該是被B-A取代而不是-AB
而這邊我想不到原因
如果不解決這問題
那上式成立的條件就是det(XY)=det(X)det(Y)
(這是我們要證明的)
因為您是用兩分塊矩陣相乘
所以我倍感困惑
希望獲得您的解答
謝謝
因為排版的問題 所以這部分我得重新以底線代替空白輸入
det |B I|=|B __I|
____|0 A|_|-AB 0|
列 左乘
左乘  的實際操作是
的實際操作是



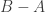 。
。
並不會產生
想請問老師, 若A,B不為square, 是否這個定理也可以用. 可否說因為若 A或 B不可逆,則 AB 也不可逆, 但等號依然成立, 所以看到Det(AB) 雖然AB不可逆, 依然可以拆解成Det(A)*Det(B)
自問自答, 根據定義算Det,只適用於square matrix. 故相關的性質都會特別強調是nxn 的square matrix
請參閱下文註解1:
A=B-1 都為n*n矩陣
det (A-1)=det(B)
不是應該為
A=B-1 ,A-1=B
det (A+1)=det(B)
A=B-1 都為n*n矩陣
det (A-1)=det(B)
不是應該為
A=B-1 ,A+1=B <===修改
det (A+1)=det(B)
Reblogged this on NewsXeon新氙事.