本文的閱讀等級:高級
定義於向量空間 的任一線性變換可以用一個
階複矩陣表示 (參考某基底)。除了少數特殊矩陣,如對角矩陣、投影矩陣、旋轉矩陣,和鏡射矩陣等,學者經常無法清楚地掌握矩陣變換的確實行為,主要原因是人們很難想像高維 (
) 向量空間,遑論向量在這些空間中的變換。欲洞察任意方陣的映射行為雖非易事,但也不是全然無跡可循,本文介紹一個認識矩陣作為的方法──透過矩陣與複數的類比來區分界定重要的特殊方陣。對複矩陣陌生的讀者,請先閱讀背景文章 “從實數系到複數系”。
複數系 和複向量空間
擁有許多相同的代數性質,例如,二者都有加法、乘法,運算規則,以及定義良好的加法單位元素
和乘法單位元素
(
空間則為零矩陣
和單位矩陣
),還有一項稱為共軛轉置。設
,
為
階複方陣,
和
滿足下面這個性質:
和
,其中
,也就是
。以複矩陣的共軛轉置 (
) 與複數的共軛 (
) 類比,可以很容易明瞭複方陣及其代表的線性變換具有何種作為與性質。(注意,純量的轉置即為其自身,
。) 複數平面上最重要的幾個子集合包括:實數集、純虛數集、正實數集,和絕對值為
的複數所形成的集合,我們將分別討論對應這四個子集合的矩陣型態。
複數 必須滿足什麼條件方為實數?答案是
。仿照這個概念可以定義「若
,則方陣
是實的 (real)。」不過沒有人會說「方陣是實的」,數學家稱它為「自伴 (self-adjoint)」。自伴一詞不常出現在基礎線性代數教科書裡;對於實矩陣,自伴其實就是我們熟悉的對稱 (symmetric),複矩陣則叫做 Hermitian。以下我們提到 Hermitian,讀者就應將它與實數聯想在一起,這能幫助我們記得 Hermitian 矩陣的一些性質。譬如,若
和
是 Hermitian 矩陣,則
也是 Hermitian;若
是 Hermitian,則
也是Hermitian,但條件是純量
為實數;若可逆矩陣
是 Hermitian,
也是 Hermitian。那麼兩 Hermitian 矩陣的乘積是否仍為 Hermitian?不對。矩陣乘法是延伸代數法則時最常出錯的地方,正確的敘述應為:
若 和
是 Hermitian,則
或
為 Hermitian 的充要條件是
和
是可交換矩陣,即
。
證明如下:若 ,則
。若
,則
。
複數 為純虛數的條件為何?答案是
。當然我們可以設想矩陣也有類似的陳述:「若
,則方陣
是純虛的 (imaginary)。」數學家稱此性質為 skew,意思是「偏斜」,實矩陣和複矩陣的對應名稱分別是斜對稱 (或反對稱,anti-symmetric) 和 skew-Hermitian。既然任意複數
可表示為
,其中
,
為實數,很自然地,我們不免好奇:任意方陣是否可分解為
,其中
是 Hermitian,
,而
是 skew-Hermitian,
?或分解為
,其中
和
都是 Hermitian 矩陣?考慮
則 且
。令
,則
。這說明任意方陣都可以分解為 Hermitian 矩陣 (對應複數的實部) 與 skew-Hermitian 矩陣 (對應複數的虛部) 之和,稱為 Hermitian 分解或卡氏 (Cartesian) 分解。
複數 為正實數的條件是什麼?
的條件是
可以表示為
,
為非零實數,或
可表為
,
為非零複數。“特殊矩陣 (9):Hermitian 矩陣”曾經介紹:若
是 Hermitian,對於任意向量
,
是實數。利用此性質再加上前述兩個複數為正實數的條件,我們也可以想像「方陣
是正的 (positive)」,如果以下任一條件成立:
(1) ,
為可逆 Hermitian 矩陣。
(2) ,
為可逆矩陣。
(3) 為 Hermitian,且對於任意非零向量
,
。
數學家最後選擇了條件 (3) 當作定義並稱它為正定 (positive definite)。正定矩陣的詳細討論請見“正定矩陣的性質與判別方法”。事實上,上述三個條件是等價的,下面證明 (1)→(2)→(3)→(1)。若 且
,則
。若
,則
,且
,因
可逆且
。若 (3) 成立,
的零空間僅有
,故
是可逆矩陣。設
的奇異值分解為
,其中
,
,
和
,則
。因為
,可以證明
(見附註[1])。令
。所以,
明顯地, 是 Hermitian。
複數 的長度為
的條件是什麼?答案是
。同樣地,如果方陣
滿足
,也就有
,此式可以解讀為「長度等於
的矩陣」。若
為實矩陣,稱為正交 (orthogonal) 矩陣;若
為複矩陣,則稱為么正矩陣或酉矩陣 (unitary)。類似絕對值為1的複數,
,么正矩陣也有三個等價的性質 (見“特殊矩陣(3):么正矩陣(酉矩陣)”):
(1)
(2) 對於任意 和
,
。
(3) 對於任意 ,
。
也就是說,么正矩陣所執行的線性變換不改變兩向量間的夾角,也不會改變向量長度。兩么正矩陣乘積亦為么正矩陣,么正矩陣的逆矩陣也為么正矩陣,這與複數性質相同。設 ,
,則
,
。
最後一個問題:複數可以用極座標表示為 ,
,
,那麼複矩陣是否也有對應的形式呢?有的,它稱為極分解 (polar decomposition),形式如
(詳見“極分解”),
是半正定矩陣,
是么正矩陣;
對應複數的長度
,
對應單位圓上的旋轉量
。極分解可由奇異值分解推導而得。設
的奇異值分解為
,對角矩陣
的主對角元皆不小於零,故
為半正定,且
,
,所以
其中 是 Hermitian 半正定,因
,而
亦為么正矩陣。另外,極分解也可表示為
,不難驗證
。
在複數平面上,與複數 相乘的意義是將長度拉伸
倍並旋轉
弧度。在向量空間
中,極分解
將線性變換
分解成拉伸
和旋轉
二部分。反過來說,從極分解也能推演出前述各個集合,作法仍是將極分解與複數極座標聯想在一起。
(1) 為實數的條件是
。若
,
是 Hermitian,因為
也是 Hermitian,前面曾經說明
要成立必須滿足乘法交換律
。
(2) 是純虛數的條件是
。若
,
是 skew-Hermitian,因為
是 Hermitian,
,故
的條件還要加上
。
(3) 為正實數的條件是
,即
。類比陳述
為半正定的條件是
,故
,所以得到
,我們說
是可么正對角化(unitarily diagonalizable),主對角奇異值矩陣
包含大於或等於零的主對角元。
(4) 的絕對值為1的條件是
,因此
為么正矩陣的條件是
,或
,這說明了
的所有奇異值為
(但
的特徵值未必為
)。
不止矩陣可以和複數類比,矩陣的特徵值根本就與所類比的複數擁有相同的性質。Hermitian 矩陣的特徵值為實數 (“特殊矩陣 (9):Hermitian 矩陣”),skew-Hermitian 矩陣的特徵值為純虛數 (“特殊矩陣 (2):正規矩陣”),正定矩陣的特徵值為正實數 (“特殊矩陣 (6):正定矩陣”),么正矩陣的特徵值其絕對值為 (“特殊矩陣 (3):么正矩陣(酉矩陣)”)。
最後我將矩陣與複數的類比整理如下 (見下表):
- Hermitian 矩陣
對應實數
;
- Skew-Hermitian 矩陣
對應純虛數
;
- 正定矩陣對應正實數
;
- 么正矩陣
對應長度為
的複數
;
- 極分解
對應複數的極座標表示
,半正定矩陣
對應長度
,么正矩陣
對應旋轉
。
附註:
[1] 因為 ,可得
。若
,則每一
使得
。下面證明
具有唯一性。假設
使得
,其中
。將
改寫為
,其中
滿足
。比較上式等號兩邊的
元,
,也就有
,或
。所以,


老師:
建議您把最後一段 “矩陣與複數的類比” 整理
改用 “表格” 方式來呈現,
可以讓讀者觀念更清晰。
謝謝!
謝謝建議,已放上類比整理表,只是解析度不佳。
建議老師把表格 Transpose
複數、矩陣:在第一列
實數、Hermitian:第二列
純虛數、skew-Hermitian:第三列
正實數、正定:第四列
單位長、酉unitary:第五列
表格只有兩欄,字級可加大,會看得更清楚!
老師你好,因為我明年就要考試了,所以想找一些清大 交大用的現性代數的原文書,能不能請老師跟我說一下書名呢??
謝謝!!!!
今天上午,用辦公室的電腦 (螢幕解析度800 x 600 ,也有切換到 1024 x 768測試), Windows環境 以 Microsoft IE 6.0 瀏覽,表格很奇怪,而且等號看起來變成減號,中文字不清楚。
回家用自己的Mac瀏覽,使用FireFox 3.6,表格看起來正常,等號及中文字也很清楚。
老師若考慮在不同作業系統、不同瀏覽軟體皆能良好呈現表格,
大概需要事先把表格的size縮小,這樣才不會在低解析度環境下,圖形被自動再縮小一次而影響解析度。
今天上午建議表格Transpose是一種方法,也許老師會有更好的方法來呈現。
To Kevin,
以下是目前各學校使用的教科書,各班可能採用不同教科書。
Gilbert Strang, Introduction to linear algebra, 4th ed., Wellesley-Cambridge Press, 2009.(交大電機,清大電機)
Howard Anton, Elementary Linear Algebra, 9th ed., John Wiley & Sons, Inc, 2005.(交大電機)
Spence, Insel, and Friedberg, Elementary Linear Algebra, 2nd ed., Pearson Education, 2008. (交大電機資訊學士班,台大電機系)
Friedberg, Insel, and Spence, Linear Algebra, 4th Ed, Prentice Hall, 2003.(清大電機系)
我在 Windows 環境以三種瀏覽器開啟本頁,結果是
google 及 ie8 —> 很清楚
firebox —> 不佳,字體破碎
你建議的方法我會再試試,謝謝。
我在Windows環境又測試,FireFox顯示正常,不會破碎。
但是ie6會有字體破碎之現象,等號變成減號。
我採用了Watt Lin 的建議:從小畫家讀入原圖PDF檔,長寬縮小後另存圖檔,再將此圖貼上(不再縮小),結果如上。從我的電腦看起來還算清晰,如果讀者仍看見破碎字體請留言告訴我。
現在用ie6來看,可以正常顯示了!
謝謝老師!效率真好。
昨日突然發覺竟然忘記將矩陣最重要的性質「特徵值」放上來比較。
我將各類型矩陣的特徵值性質補充於後,並加註引用來源,之前做好的表也跟著修改了。
「特徵值」放進來,
這樣,愈看愈有趣了!
complex number 可同构为2dimensional Conformal linear transformation
complex number 可同构为2dimensional Conformal linear transformation
是的。詳見’解讀複數特徵值’
講這個的話應該可以提一下數值域(numerical range),就可以完整的對到複數
有個地方有一點疑問,3推1的時候A做了svd分解,為什麼A=A*可以得到U=V? 個人在證3到1時是使用A is self adj ,則存在一組. Orthon eingenbase(unitary equav to diag matrix)在利用其eingenvalue大於0之後就跟老師一樣了
若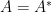 ,則
,則  可正交對角化為
可正交對角化為  ,其中
,其中 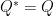 ,
,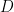 是對角矩陣。
是對角矩陣。
老師的意思是說A=A*,則A的svd是唯一的嗎.可是一矩陣的svd不是唯一不是嗎,而且如果A=A*則保證它的svd剛好是unitary equav to diag matrix嗎 ?
原來是這樣想A*A是半正定,在算他的長相,也知道那樣令B會是半正定(事實上是正定),因為(sigma)是正定,算出來A^2=B^2,在利用那招便知道A=B,最後V and sigma is invertiable變的到結論 這一招很漂亮呢 多了一種3到一的看法
感謝老師
我們要證明的是 ,這與SVD的唯一性無關。
,這與SVD的唯一性無關。
原來是這樣想A*A是半正定,在算他的長相,也知道那樣令B會是半正定(事實上是正定),因為(sigma)是正定,算出來A^2=B^2,在利用那招便知道A=B,最後V and sigma is invertiable變的到結論 這一招很漂亮呢 多了一種3到一的看法
感謝老師