本文的閱讀等級:高級
理解線性變換 的一個有效方式是透過解釋其幾何意義來呈現從向量空間
經過線性變換
映射至向量空間
的變化性質。實際作法可由兩方面著手,第一個作法是在輸入空間
和輸出空間
中分別挑選出適當的基底,藉由基底之間的映射關係解析線性變換
,這個結果稱為對角化;第二個作法是固定輸入向量
的某些幾何性質,從觀察輸出向量
的變化情況來瞭解
的作用。本文採用上述兩種方法解說奇異值分解 (singular value decomposition,簡稱 SVD) 的幾何意義 (見“奇異值分解 (SVD)”)。
奇異值分解是一個相當重要的矩陣分解式,在訊號處理和統計分析尤其有廣泛的應用。令 為一個
階實線性變換表示矩陣,且
。(本文將討論範圍限於實矩陣,如要推廣至複矩陣只須將轉置運算
替換為共軛轉置
即可。) 奇異值分解常出現於兩種問題形式,第一是約束最佳化 (constrained optimization) 問題:考慮單位輸入向量
,
,求最長的輸出向量
,即
第二是較為一般性的輸出界定問題:同樣設 ,求
的所有可能範圍。毫無疑問,我們選擇從較為單純的約束最佳化問題下手。
輸出向量 的長度平方算式可推得下面的二次型:
這說明 階交互乘積
是實對稱半正定矩陣。既然
由
決定,於是我們將焦點集中在此方陣上。考慮特徵方程式
實對稱矩陣 擁有單範正交 (orthonormal) 特徵向量,即
若
,且對任意
,
。另外,半正定矩陣的特徵值不為負數,故可設
。綜合以上結果,
可正交對角化為
其中 ,
為正交矩陣,
。接著我們利用變數變換來化簡二次型,令
,就有
正交變換 不改變向量長度,直接計算確認
原本問題等價於下面這個簡約問題:
展開二次型並利用已知條件:
於是解得
最大值發生於 ,亦即
指向對應最大特徵值的特徵向量。
回答了第一個問題後,我們繼續往下深入探討。考慮單範正交向量集 為
的一組基底。當
時,
假設 包含
個非零特徵值,遞減排序如
,
。當
,
,而當
,
。這個結果極富啟發性,它提供了基底向量
經過線性變換
之後的長度大小變化,我們定義矩陣
的奇異值 (singular value) 為
奇異值也按遞減方式排序, 且
。在
空間,我們得到
個不為零的基底映射
,
。若
,
推知 是一組正交向量集,可作為矩陣
的行空間基底,因此
。對於
,將
予以正規化,令
整理前述基底映射結果,就有
下圖表示 的基底向量
經線性變換
後映至
的結果,有兩點值得特別注意:對於
,
,而且
彼此互為正交。
將上述二組方程式整理成矩陣形式,如下:
設 階矩陣
,
為
階矩陣,
,所以
上式等號兩邊同時右乘 便得到
的奇異值分解:
奇異值分解其實是一種矩陣對角化形式。操作 Gram-Schmidt 正交化程序可將向量集 擴充為
的一組單範正交基底
,對應的
矩陣因此成為
階正交矩陣,
,同時又在
底下增加
列零元使成為
階矩陣,
。令
,代入奇異值分解式,
,等號兩邊左乘
得到
令 ,
可以解釋為
參考
基底
的座標向量,表示為
。同樣道理,
也可以解讀為
參考
基底
的座標向量,
。經對角化後,以座標向量
和
表達的變換關係格外簡單:
。
現在我們可以輕易解決輸出向量 的範圍問題。設
階矩陣
為
其中 ,
為
階方陣,因此,
上式等號兩側分別計算向量長度平方,左邊是
右邊是
合併二式得到不等式:
當 時,輸出向量
的軌跡由一個
維橢圓體所包覆,
指向最長軸其軸半徑為
,而
則指向最短軸其軸半徑為
。
下面我們用一例說明,考慮
交互乘積為
奇異值分解的詳細計算步驟如下:
(1) 解出 的特徵值,奇異值與特徵向量:
,
,
,可知
,
,
,對應的特徵向量經正規化後分別為
(2) 隨即得出正交矩陣 和奇異值矩陣
:
(3) 計算 ,
:
合併即得
總結:線性變換 的映射行為可從正交基底的關係解釋,見下圖。
(1) 當 ,輸出
對應橢圓長軸半徑。
(2) 當 ,輸出
對應橢圓短軸半徑。
(3) 當 ,輸出為零向量。



http://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D++%5CVert+A%5Cmathbf%7Bv%7D_i%5CVert%5E2%26%3D%5Cmathbf%7Bv%7D_i%5ETA%5ETA%5Cmathbf%7Bv%7D_i%3D%5Cmathbf%7Bv%7D_i%5E%7BT%7D%5Clambda_i%5Cmathbf%7Bv%7D_i%3D%5Clambda_i%5Cend%7Baligned%7D&bg=ffffff&fg=333333&s=0
請問是怎麼推得當 x=v_i 時有這個等式的呢
最初推論就已經設 是
是 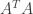 的特徵向量對應特徵值
的特徵向量對應特徵值 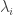 ,即
,即


所以
你好
奇異値分解的三個矩陣,要怎麼用簡短的中文各自描述它們呢?
簡單講就是將給定的矩陣A「對角化」,將A看成線性變換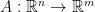 ,
, 的行向量構成
的行向量構成 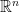 的基底,
的基底, 的行向量構成
的行向量構成 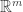 的基底,
的基底, 將
將  映射至
映射至 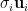 。請參閱下文:
。請參閱下文:
教授您好,想要再請教您:
藉由m×n非方陣A的交乘矩陣A^TA所具備的對稱半正定性,我們一定可以得到對角化SVD,
那麼為什麼我們不乾脆同樣藉由n×n方陣A的交替矩陣A^TA(一樣會具備對稱半正定性)來求得diagonalization,而是轉而分析n×n方陣A的eigenspace、eigenvectors等等,而這甚至還不保證方陣可以diagonalization?
懇請教授賜教,謝謝~~~
SVD(對角化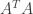 )與譜分解(對角化
)與譜分解(對角化 )各自有不同的應用,
)各自有不同的應用,
教授您好,不知道我是否有問錯問題??
我的問題是指……任意m×n非方陣既然能藉由其交乘矩陣的”對稱半正定性”來得到對角化SVD
那怎麼會有一些n×n方陣無法diagonalization呢?
n×n方陣的交乘矩陣同樣會有對稱半正定性,照理來講似乎也可以SVD,
而方陣的SVD結果不就是diagonalization嗎??
為什麼會出現這樣的矛盾呢?
或者是我有什麼地方認知錯誤嗎?
懇請教授賜教,謝謝
教授您好,我猜想我誤解的點可能是在於,針對一個n×n方陣做SVD,分解式中的U和V也是兩組不同的orthonormal basis(雖然dimension一樣是n),然而真正的diagonalization則是必須在同一組orthonormal basis中達成……n×n方陣的SVD只能說是看起來好像是diagonalization實則不然???
是的,當你花90%的力氣弄清楚問題,只要10%的力氣就得到答案。
對角化是來自 ,所有的
,所有的  組成完成整的線性獨立集。
組成完成整的線性獨立集。 ,我們總是能找到 orthonormal
,我們總是能找到 orthonormal  。
。
SVD來自
謝謝教授指導,我明白了~
半夜12:25看著這篇的我內心湧現許多熱血,醍醐灌頂,太感動了。