本文的閱讀等級:中級
具有內積功能的向量空間簡稱為內積空間,線性代數中許多重要理論和應用都從內積空間衍生出來,例如基底正交化,QR 分解,最小平方法,矩陣譜定理,甚至奇異值分解 (singular value decomposition) 也和內積空間密切相關。在內積空間中,最重要的運算除了內積本身,另一個威力強大的代數工具就是將任意向量分解為正交分量之和的正交投影 (orthogonal projection)。本文介紹兩個推導正交投影矩陣方法,第一個是歸納法,從一道簡單的幾何問題開始──將向量投影至一直線,繼續推廣可導出至一般子空間的正交投影。這個方法較具幾何直觀,適宜初學者學習。另一個方法是將正交性質加入向量空間的斜投影,再利用矩陣代數推導正交投影矩陣。本文內容限定實幾何向量空間 ,如欲延伸至
,僅需將轉置
改為共軛轉置
。
見下圖,考慮 中兩向量
和
,直線
由
所生成 (span),如何計算
至直線
的正交投影?請注意本文的向量皆為行向量 (column vector)。
令 為投影量,
是待決定的純量。根據正交投影的定義,殘餘量
必定與
正交 (垂直),亦即
與
的內積為零,
。
展開上式得到唯一解 。使用矩陣乘法結合律,
,
其中 是一個
階矩陣,稱為外積 (outer product)。令
為
階投影方陣滿足
。上式表明
。
向量 可分解為投影至直線
的分量
與殘餘量
,且
。殘餘量
屬於正交補餘
,
也就是
的正交投影矩陣。
運用同樣方法可以將向量 正交投影至線性獨立向量集
所生成的子空間
。設正交投影量為
,
由正交條件決定:
,
。令
階矩陣
。寫出
,其中
,上述
個條件式可表示成矩陣形式,如下:
,
整理得到 。因為
有線性獨立的行向量,
。再利用實矩陣秩性質
(見“利用 Grammian 矩陣證明行秩等於列秩”),得知
是
階可逆方陣,
有唯一解:
,
也就得出正交投影量
。
上式同時給出了正交投影至子空間 的
階方陣:
。
同樣地,至正交補空間 的正交投影矩陣為
。
若 ,則
階矩陣
有
個線性獨立的行向量。在此情況下,
為可逆方陣,故
。若
,
未定義,不過我們仍可推斷
。
下面我們介紹另一個推演正交投影矩陣的方法。在“直和與投影”一文,我們導出了在向量空間 中沿著
至
的投影矩陣,設
為
的基底,而
為
的基底。令
階可逆矩陣
。
斜投影矩陣算式為
。
接下來的工作是在正交投影的條件下計算 ,亦即解出
階矩陣
和
階矩陣
使得
。
以分塊矩陣乘法展開可得 ,
,
,
。
是
的左逆矩陣,
是
的左逆矩陣。
在一般情況下, 和
並不具有簡單公式,但如果
為正交投影矩陣,則可以化簡得
,
公式。若
是
的正交補餘,
,也就是說,對於任意
,
,
,以矩陣乘法表示為
,
取轉置也有 。又因為
和
的行向量都是線性獨立的,故
,
,
和
皆為可逆矩陣。綜合以上結果,不難驗證
因此,
。
代入斜投影矩陣計算公式便導出正交投影矩陣:
。
我們可以證明正交投影矩陣 與
的行空間 (column space) 關係為
且零空間 (nullspace) 關係為
。若
,則
,故
,證明
。若
,必存在
使得
,換句話說,
通過
正交投影至
,故
,證明
。合併以上結果,
。使用子空間的正交補餘關係,
與
。又因為
且
,推得
。
最後還要強調一點,不論是斜投影或正交投影,投影矩陣 與選擇的基底無關。假設兩個線性獨立向量集
和
都生成出相同的子空間,這表示任意
可以唯一表示成
的線性組合,亦即存在唯一的
階可逆矩陣
滿足
。
將上式代入正交投影矩陣,可得
例如,向量空間 的子空間
有兩組基底:
由基底 計算出投影矩陣為
,
由基底 計算出投影矩陣為
,
確認 。
顯然基底 給出較為簡單的算式,這個結果建議我們選擇正交基底。如果
包含正交行向量,
為對角矩陣
,就有
採用正交基底的優點是正交投影量的計算非常簡單,利用乘法結合律可得
又如果 包含單範正交 (orthonormal) 行向量
,其中
若
,
若
,就有
,
投影矩陣因此為
正交投影量則為
。
欲進一步瞭解正交投影矩陣的性質,請參見“特殊矩陣 (5):冪等矩陣”。正交投影於最小平方法的應用,請見“從線性變換解釋最小平方近似”。正交投影與基底正交化,QR 分解,和矩陣譜定理的關係將另文說明。


不好意思能夠協助解此題嗎
Let A has three columns
(1, 1,…, 1),
( t1,t2,t3…tm) ,
( [t1]^2, [t2]^2, [t3]^2, …[tm]^2 )
Solve (AT)Ax = (AT)b
(AT)為A的轉置矩陣
你的問題稱為 polynomial curve fitting,概念很簡單但計算很繁雜,這個網站裡面說明的很清楚:
http://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html
如果你有其他問題可以在交流園地發表,謝謝。
最近看youtube上量子力學開放課程的lectures,發現正交基底及正交投影矩陣的概念在量子力學的數學描述大量的使用,正交投影果然是威力強大.
周老师,如果空间再一般一些,该如何做投影呢?比如该空间为Ax=b.
我的方法就是构造一个优化问题 min norm(s-x) s.t. Ax = b
可是物理意义不是很明显。 周老师可以妙法?
你說的仿射空間的投影問題, 譬如說:給定 ,
,  是一向量空間,
是一向量空間,  是
是  的子空間,
的子空間,  是子空間
是子空間  再加上平移
再加上平移 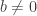 , 我們想找出
, 我們想找出 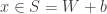 使得
使得  極小.
極小.
用點技巧, 先將 和
和  全都減去
全都減去  , 這樣大家又都回到子空間來. 我們默想
, 這樣大家又都回到子空間來. 我們默想
 ,
,  ,
, 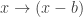
 是
是  至
至  的正交投影, 那
的正交投影, 那 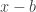 也就是
也就是  至
至  的正交投影, 由上文給出方法可得正交投影至
的正交投影, 由上文給出方法可得正交投影至  的矩陣
的矩陣  , 所以
, 所以
 推得
推得  即為
即為  中最接近
中最接近  的向量.
的向量.
既然
这个倒是个不错的直观观点。谢谢周老师。
周老師請問一下:
正交投影矩陣為甚麼只能用在歐式空間且要求標準內積呢?
正交投影並不是只能應用於具有標準內積的歐氏幾何座標空間,正交投影適用於任何有限維或無限維內積空間 (賦予內積定義的向量空間),請參見下文:
兩個著名的非歐氏空間例子:
Legendre 多項式:
傅立葉級數:
所以任何空間的投影向量皆可由P = A(A^HA)^-1A^H此矩陣算出來?
即Proj b = P*b??
是的,但前提是(1) 是有限維內積空間,(2)能夠找到一組標準正交(orthonormal)基底
是有限維內積空間,(2)能夠找到一組標準正交(orthonormal)基底 。任一
。任一 可表示為
可表示為



 是
是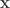 參考
參考 的座標向量,
的座標向量,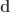 是
是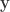 參考
參考 的座標向量。這樣你便將問題從原始向量空間
的座標向量。這樣你便將問題從原始向量空間 轉移至幾何座標空間
轉移至幾何座標空間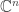 ,從此可以用MATLAB實現矩陣運算。一旦找出正交投影
,從此可以用MATLAB實現矩陣運算。一旦找出正交投影 ,也就得到原始空間的對應向量
,也就得到原始空間的對應向量 。
。
所以內積為
其中
周老师您好,补充几点:(修正下公式显示,烦请周老师删除上一天评论)
1. 方法一推广至子空间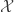 的过程中,在条件式表示为矩阵形式的公式中,向量
的过程中,在条件式表示为矩阵形式的公式中,向量 漏写了转置上标
漏写了转置上标 。
。
2. 方法一从对直线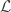 的投影到对子空间
的投影到对子空间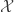 的投影的推广过程中,为保持前后统一,利用正交性质时,对于前者可直接使用
的投影的推广过程中,为保持前后统一,利用正交性质时,对于前者可直接使用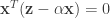 ,而不是
,而不是 ,这样后续的推导可省去对内积交换律
,这样后续的推导可省去对内积交换律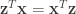 的使用。
的使用。
3. 针对正交投影矩阵 ,显然因为
,显然因为 具有线性独立column vectors,所以
具有线性独立column vectors,所以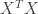 是对称可逆方阵。如果
是对称可逆方阵。如果 本身为可逆方阵(
本身为可逆方阵( ),则此时投影矩阵
),则此时投影矩阵 可化简为单位矩阵:
可化简为单位矩阵: ;但对于普通矩形矩阵(rectangular matrix)而言,上式不能进行简化,因为矩形矩阵
;但对于普通矩形矩阵(rectangular matrix)而言,上式不能进行简化,因为矩形矩阵 的逆矩阵
的逆矩阵 不存在。
不存在。
非常謝謝你。
1. 已訂正。
2. 這樣確實簡單多了。
3. 這段討論已加進內文。
想請教一下老師
在幾何上,一個orthomal矩陣,是不是就代表了一個旋轉矩陣?
更正 orthonormal矩陣
你說的是orthogonal matrix(正交矩陣)?
旋轉矩陣確實是正交矩陣,但其行列式值為1,請見
Pingback: 正交投影──威力強大的線代工具 | 線代啟示錄 | Cruise
老師您好,
請問1×1的矩陣是否能直接視為純量呢?
對於alpha=(x^tz)/(x^tx)的寫法有點疑惑。