相似變換下的不變性質

本文的閱讀等級：初級

令 $A$ 和 $B$ 為 $n\times n$ 階實 (或複) 矩陣。若存在一個可逆矩陣 $M$ 使得 $B=M^{-1}AM$ ，我們稱 $B$ 相似於 $A$ ，並稱 $M$ 為 $A$ 與 $B$ 之間的相似變換矩陣。根據定義，兩個相似矩陣具有甚麼關係？已知 $M$ 是一個 $n\times n$ 階可逆矩陣， $M$ 的行向量 (column vector) $\mathbf{m}_1,\ldots,\mathbf{m}_n$ 是線性獨立的，因此可當作 $\mathbb{R}^n$ (若是複矩陣則為 $\mathbb{C}^n$ ) 的一組基底，記為 $\boldsymbol{\beta}=\{\mathbf{m}_1,\ldots,\mathbf{m}_n\}$ 。令 $[\mathbf{x}]_{\boldsymbol{\beta}}=M^{-1}\mathbf{x}$ 代表向量 $\mathbf{x}$ 參考基底 $\boldsymbol{\beta}$ 的座標向量。考慮矩陣 $A$ 所代表的線性變換 $T(\mathbf{x})=A\mathbf{x}$ ，同樣令 $[T(\mathbf{x})]_{\boldsymbol{\beta}}=M^{-1}(A\mathbf{x})$ 代表 $T(\mathbf{x})$ 參考基底 $\boldsymbol{\beta}$ 的座標向量。將 $\mathbf{x}=M[\mathbf{x}]_{\boldsymbol{\beta}}$ 代入前式，

$[T(\mathbf{x})]_{\boldsymbol{\beta}}=M^{-1}AM[\mathbf{x}]_{\boldsymbol{\beta}}$ 。

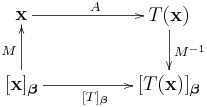
上式指出如果 $A$ 是線性變換 $T$ 參考標準基底的表示矩陣，則相似變換 $M^{-1}AM$ 即為 $T$ 參考基底 $\boldsymbol{\beta}$ 的線性變換表示矩陣 $[T]_{\boldsymbol{\beta}}$ (關於線性變換表示矩陣的深入討論可參閱“基底變換”)，這是線性代數裡一個非常重要的觀念，讀者務必完全理解。下圖顯示相似變換和線性變換表示矩陣的關係：

矩陣的對角化是最常見的一種相似變換，其形式為 $\Lambda=S^{-1}AS$ ，其中對角矩陣 $\Lambda=\mathrm{diag}(\lambda_1,\ldots,\lambda_n)$ 的主對角元為 $A$ 的特徵值，而特徵向量矩陣 $S$ 的行向量為 $A$ 的線性獨立特徵向量，可知 $S$ 是可逆的。對角化的意義是當矩陣的特徵向量是線性獨立時，參考這些特徵向量所組成基底的線性變換表示矩陣就是具有最簡約形式的對角矩陣 $\Lambda$ 。常係數微分方程是矩陣對角化的一個典型應用，考慮以下的線性系統

$\displaystyle\frac{d\mathbf{u}}{dt}=A\mathbf{u}$ 。

求解的關鍵步驟在於將變數向量 $\mathbf{u}$ 置換為 $\mathbf{u}=S\mathbf{v}$ ，代入上式，

$S\displaystyle\frac{d\mathbf{v}}{dt}=AS\mathbf{v}$ ，

左乘 $S^{-1}$ ，可得

$\displaystyle\frac{d\mathbf{v}}{dt}=S^{-1}AS\mathbf{v}=\Lambda\mathbf{v}$ 。

這是我們能夠得到最簡約的形式──完全分離所有的變數，原方程式因此分解為 $n$ 個獨立的單變數微分方程，如下：

$\displaystyle\frac{dv_i}{dt}=\lambda_iv_i,~~i=1,2,\ldots,n$ 。

回到相似變換的討論。相似關係是一種矩陣之間的等價關係 (equivalence relation)，滿足下面三個性質：

反身性：因為 $A=I^{-1}AI$ ，任意矩陣 $A$ 與其自身相似。
對稱性：若 $B=M^{-1}AM$ ，立刻有 $A=MBM^{-1}$ 。如果 $B$ 相似於 $A$ ，也就有 $A$ 相似於 $B$ 。
傳遞性：若 $B=M^{-1}AM$ 且 $C=N^{-1}BN$ ，則 $C=N^{-1}M^{-1}AMN=(MN)^{-1}A(MN)$ 。如果 $B$ 相似於 $A$ ， $C$ 相似於 $B$ ，則 $C$ 也相似於 $A$ 。

如同任一種等價關係，相似關係將 $n\times n$ 階矩陣區分為不相交的等價分類。每一個等價分類中的矩陣彼此相似，但屬於不同等價分類的矩陣則不相似。同屬於一個等價分類的相似矩陣享有許多重要的性質，也可說是相似變換下的不變性質，下面我們一一介紹這些性質。

性質一：若 $B$ 相似於 $A$ ，則 $B$ 與 $A$ 有相同的特徵多項式。

將 $B=M^{-1}AM$ 代入 $B$ 的特徵多項式 $p_B(t)=\mathrm{det}(tI-B)$ ，就有

$\begin{aligned} p_B(t)&=\det(tM^{-1}M-M^{-1}AM)\\ &=\det(M^{-1}(tI-A)M)\\ &=(\det M^{-1})\det(tI-A)(\det M)\\ &=\det(tI-A)=p_A(t).\end{aligned}$

因為特徵值是特徵多項式的根，性質二是性質一的必然結果。

性質二：若 $B$ 相似於 $A$ ，則 $B$ 與 $A$ 有相同的特徵值。

設特徵方程式為 $A\mathbf{x}=\lambda\mathbf{x}$ ，以 $A=MBM^{-1}$ 代入上式，

$MBM^{-1}\mathbf{x}=\lambda\mathbf{x}$ ，

等號兩邊左乘 $M^{-1}$ ，

$B(M^{-1}\mathbf{x})=\lambda(M^{-1}\mathbf{x})$ 。

雖然 $B$ 和 $A$ 有相同的特徵值 $\lambda$ ，但 $B$ 的特徵向量為 $M^{-1}\mathbf{x}$ ，此即 $\mathbf{x}$ 參考基底 $\boldsymbol{\beta}$ 的座標向量 $[\mathbf{x}]_{\boldsymbol{\beta}}$ 。

行列式是所有特徵值的積，跡數 (trace) 是所有特徵值的和，性質三是性質二的必然結果。

性質三：若 $B$ 相似於 $A$ ，則 $\mathrm{det}B=\mathrm{det}A$ 且 $\mathrm{trace}B=\mathrm{trace}A$ 。

下一個性質是關於矩陣秩。

性質四：若 $B$ 相似於 $A$ ，則 $\mathrm{rank}B=\mathrm{rank}A$ 。

對任意矩陣左乘或右乘一個可逆矩陣不改變原矩陣的秩，故

$\mathrm{rank}A=\mathrm{rank}(M^{-1}AM)=\mathrm{rank}B$ 。

下面提供詳細的向量空間分析證明。設 $M$ 為一可逆矩陣使得 $AM=MB$ 。若 $\mathbf{y}$ 屬於 $B$ 的行空間，記為 $\mathbf{y}\in C(B)$ ，即存在 $\mathbf{x}$ 滿足 $\mathbf{y}=B\mathbf{x}$ ，則 $AM\mathbf{x}=MB\mathbf{x}=M\mathbf{y}$ 意味 $M\mathbf{y}\in C(A)$ 。換句話說， $\mathbf{y}$ 屬於 $M^{-1}\left(C(A)\right)=\{M^{-1}\mathbf{z}\vert \mathbf{z}\in C(A)\}$ ，推得

$C(B)\subseteq M^{-1}\left(C(A)\right)$ 。

因為 $M$ 是一可逆線性變換， $\dim M^{-1}\left(C(A)\right)=\dim C(A)$ 。所以， $\text{rank}B\le\text{rank}A$ 。利用相似變換的對稱性，立知 $\hbox{rank}A\le\hbox{rank}B$ 。合併上面結果，證明 $\hbox{rank}A=\hbox{rank}B$ 。

下面還有幾個性質留給讀者朋友當作練習。

若 $B$ 相似於 $A$ ， $p(t)$ 為一多項式，則 $p(B)$ 相似於 $p(A)$ 。
若 $B$ 相似於 $A$ ，則 $B+cI$ 相似於 $A+cI$ ， $c$ 是一個純量。
若 $B$ 相似於 $A$ ，相似變換矩陣為 $M$ ， $D$ 相似於 $C$ ，相似變換矩陣也為 $M$ ，則 $B+D$ 相似於 $A+C$ 。

最後，我們希望在等價分類中挑出一個矩陣作為該分類的「代表」，並主張每一個等價分類存在唯一的代表，不同的等價分類則有不同的代表。如此一來，藉由檢查矩陣 $B$ 所屬的分類代表是否與 $A$ 所屬的分類代表相同，即可判斷 $B$ 是否相似於 $A$ 。主對角特徵值矩陣 $\Lambda$ 似乎是個不錯的選擇，但不幸地，並非所有的 $n\times n$ 階矩陣都可以被對角化。不可對角化發生於該矩陣有重複 $p$ 次的特徵值 ( $p$ 稱為代數重數)，但卻僅存在 $q$ 個線性獨立的特徵向量 ( $q$ 稱為幾何重數)， $q<p$ 。線性獨立的特徵向量湊不滿 $n$ 個，這些特徵向量無法構成 $\mathbb{R}^n$ (複向量則為 $\mathbb{C}^n$ ) 的一組基底。退而求其次，在每一個等價分類中，我們仍然能找到一個特殊矩陣，它非常接近主對角特徵值矩陣並滿足等價分類矩陣家族「代表」所必須具備的性質，稱之為 Jordan 典型形式 (詳見“Jordan 典型形式淺說 (上)”)。整理本文得到的結論，相似變換下的主要幾個不變性質有：特徵多項式、特徵值、行列式、跡數、矩陣秩以及 Jordan 形式。

2 Responses to 相似變換下的不變性質

matrix67 says:

12/17/2013 at 5:20 pm

老師您好，相似矩陣有相同的列空間和零空間嗎？因為相似矩陣是同一個線性變換T在不同基底下的矩陣，所以直觀上來想相似矩陣的列空間應該都是Im(T),零空間都是Ker(T)。但是事實似乎不是的，那麼如何理解這個問題呢，同時哪一個矩陣的列空間與零空間和線性變換的image&Kernel是相同的呢？

- ccjou says:
  
  12/17/2013 at 6:26 pm
  
  這二個問題有點意思，我再另文詳述，回覆會貼在「答讀者問」。
  
  另外，你說的「列空間」在台灣稱作「行空間」，詳見
  
  兩岸線性代數用詞參照
  
  台灣仍沿襲古代中文用法──直為行，《九章算術》曰：以右行上禾遍乘中行而以直除。見下文
  
  《九章算術》的方程術

	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明
	悟 on 條件機率與貝氏定理
	jeremy on 內積與外積是怎麼來的？