答matrix67──關於二相似矩陣的行空間與零空間的關係

網友matrix67留言：

老師您好，二相似矩陣有相同的列空間和零空間嗎？因為二相似矩陣是同一個線性變換 $T$ 在不同基底下的表示矩陣，所以直觀上來想二相似矩陣的列空間應該都是 $\text{im}(T)$ ，零空間都是 $\ker(T)$ 。但是事實似乎不是的，那麼如何理解這個問題呢？同時那一個矩陣的列空間與零空間和線性變換的 image 與 kernel 是相同的呢？

答曰：

首先我說明矩陣基本子空間的命名規則。在台灣，橫向稱為列，縱向稱為行。在中國大陸，橫向稱為行，縱向稱為列。以下討論沿用台灣的慣例，也就是說，問題中的「列空間」改成「行空間」。給定一個 $m\times n$ 階實矩陣 $A$ ，對應的四個基本子空間記為：行空間 (column space) $C(A)$ ，列空間 (row space) $C(A^T)$ ，零空間 (nullspace) $N(A)$ ，和左零空間 (left nullspace) $N(A^T)$ 。在向量空間 $\mathbb{R}^m$ 中， $N(A^T)$ 是 $C(A)$ 的正交補餘；在向量空間 $\mathbb{R}^n$ 中， $C(A^T)$ 是 $N(A)$ 的正交補餘 (見“線性代數基本定理 (二)”)。因為這個緣故，我們只須專注於行空間和零空間。另外，以下內容如欲延伸至複矩陣，將轉置 $(\cdot)^T$ 替換為共軛轉置 $(\cdot)^\ast$ 即可。

令 $A$ 和 $B$ 為 $n\times n$ 階矩陣。如果存在一個可逆矩陣 $M$ 使得 $A=MBM^{-1}$ ，我們稱 $A$ 相似於 $B$ ，並稱 $M$ 為 $A$ 和 $B$ 之間的相似變換矩陣。相似變換是一種等價關係，許多重要的矩陣性質維持不變，如特徵值、行列式、跡數、矩陣秩，以及 Jordan 形式 (見“相似變換下的不變性質”)。

兩個相似矩陣的行空間和零空間是否相同？先看一個特殊情況。如果 $A$ 是一個純量矩陣，即 $A=cI$ ，這裡 $c$ 是任何數， $I$ 是單位矩陣，則 $B=M^{-1}AM=M^{-1}(cI)M=cI=A$ 。任一純量矩陣僅與其自身相似，純量矩陣的「相似家族」(包含與其相似的所有矩陣) 只有一個成員，自然所有的矩陣性質維持不變。除了純量矩陣外，任何矩陣 $A$ 所屬的「相似家族」必定包含無窮多個成員 (因為相似變換矩陣 $M$ 可隨意選擇)。

以下考慮非純量矩陣，分開兩個情況討論。若 $A$ 是可逆矩陣， $\text{rank}A=n$ ，則 $C(A)=\mathbb{R}^n$ 且 $N(A)=\{\mathbf{0}\}$ 。如果 $B$ 相似於 $A$ ，則 $\text{rank}B=\text{rank}A$ ，也就有 $C(B)=\mathbb{R}^n$ 且 $N(B)=\{\mathbf{0}\}$ 。因此，每一個可逆矩陣所屬的「相似家族」的行空間為 $\mathbb{R}^n$ ，零空間為 $\{\mathbf{0}\}$ 。若 $A$ 是不可逆矩陣， $\text{rank}A<n$ ，那麼 $B=M^{-1}AM$ 和 $A$ 是否也有相同的行空間和零空間？答案是否定的。很容易舉出反例，譬如， $A=\begin{bmatrix} 1&0\\ 0&0 \end{bmatrix}$ ， $M=\begin{bmatrix} 0&1\\ 1&0 \end{bmatrix}$ ，可得 $B=M^{-1}AM=\begin{bmatrix} 0&0\\ 0&1 \end{bmatrix}$ ，也就有

$\displaystyle C(A)=\text{span}\left\{\begin{bmatrix} 1\\ 0 \end{bmatrix}\right\},~~ N(A)=\text{span}\left\{\begin{bmatrix} 0\\ 1 \end{bmatrix}\right\},$

$\displaystyle C(B)=\text{span}\left\{\begin{bmatrix} 0\\ 1 \end{bmatrix}\right\},~~ N(B)=\text{span}\left\{\begin{bmatrix} 1\\ 0 \end{bmatrix}\right\}$ 。

對於不可逆矩陣 $A$ ，如何理解 $B=M^{-1}AM$ 和 $A$ 有不同的行空間和零空間？這個問題可以拆解為兩個子問題： $M^{-1}A$ 和 $A$ 的行空間以及零空間有甚麼關係？ $AM$ 和 $A$ 的行空間以及零空間又有甚麼關係？因為 $M$ 是可逆矩陣，下面性質成立 (相關討論見“矩陣乘積的子空間分析”)：

$C(AM)=C(A)$

若 $\mathbf{x}\in C(A)$ ，則存在 $\mathbf{y}$ 使得 $\mathbf{x}=A\mathbf{y}$ 。令 $\mathbf{z}=M^{-1}\mathbf{y}$ 。合併前面兩式，可得 $\mathbf{x}=AM\mathbf{z}$ ，故 $\mathbf{x}\in C(AM)$ 。若 $\mathbf{x}\in C(AM)$ ，則存在 $\mathbf{z}$ 使得 $\mathbf{x}=AM\mathbf{z}$ 。令 $\mathbf{y}=M\mathbf{z}$ 。合併前面兩式，可得 $\mathbf{x}=A\mathbf{y}$ ，故 $\mathbf{x}\in C(A)$ 。

$N(M^{-1}A)=N(A)$

若 $\mathbf{x}\in N(A)$ ，即 $A\mathbf{x}=\mathbf{0}$ ，左乘 $M^{-1}$ ，可得 $M^{-1}A\mathbf{x}=\mathbf{0}$ ，故 $\mathbf{x}\in N(M^{-1}A)$ 。若 $\mathbf{x}\in N(M^{-1}A)$ ，即 $M^{-1}A\mathbf{x}=\mathbf{0}$ ，左乘 $M$ ，可得 $A\mathbf{x}=\mathbf{0}$ ，故 $\mathbf{x}\in N(A)$ 。

另一方面，如前例所示，存在一個可逆矩陣 $M$ 使得

$\displaystyle C(M^{-1}A)\neq C(A),~~N(AM)\neq N(A)$ 。

以上結果說明

$\displaystyle C(M^{-1}AM)\neq C(AM)=C(A),~~N(M^{-1}AM)=N(AM)\neq N(A)$ 。

兩個相似不可逆矩陣有不同的行空間和零空間，但它們之間是否存在某種關係？我們可以從線性變換表示矩陣來探討這個問題。令 $\mathcal{V}$ 為一個有限維向量空間， $\dim \mathcal{V}=n$ ，且 $T:\mathcal{V}\to\mathcal{V}$ 為一個線性算子。假設 $\boldsymbol{\beta}=\{\mathbf{v}_1,\ldots,\mathbf{v}_n\}$ 是 $\mathcal{V}$ 的一組基底。對於每一 $\mathbf{x}\in\mathcal{V}$ ，存在唯一數組 $(c_1,\ldots,c_n)$ 使得 $\mathbf{x}=c_1\mathbf{v}_1+\cdots+c_n\mathbf{v}_n$ 。習慣上，我們將 $\mathbf{x}$ 參考基底 $\boldsymbol{\beta}$ 的座標向量記作 $[\mathbf{x}]_{\boldsymbol{\beta}}=(c_1,\ldots,c_n)^T$ 。明顯地，向量 $\mathbf{x}\in\mathcal{V}$ 和座標向量 $[\mathbf{x}]_{\boldsymbol{\beta}}\in\mathbb{R}^n$ 有一對一的對應關係，我們說座標映射 $[\cdot]_{\boldsymbol{\beta}}$ 是一個同構映射 (isomorphism)。從向量空間的層次來說，向量空間 $\mathcal{V}$ 和幾何座標空間 $\mathbb{R}^n$ 是同構的 (見“同構的向量空間”)，記為 $\mathcal{V}\cong\mathbb{R}^n$ 。淺白地說，蘋果和橘子不同，但如果蘋果和橘子具有一對一的對應關係 (譬如，每一顆蘋果和每一個橘子都貼上號碼)，那麼我們說一箱蘋果和相同數量的一籃橘子是同構的。假設

$\displaystyle T(\mathbf{v}_j)=a_{1j}\mathbf{v}_1+\cdots+a_{nj}\mathbf{v}_n,~~j=1,\ldots,n$ ，

則線性算子 $T$ 參考 $\boldsymbol{\beta}$ 的表示矩陣為 (見“線代膠囊──線性變換表示矩陣”)

$\displaystyle A=[T]_{\boldsymbol{\beta}}=\begin{bmatrix} a_{11}&\cdots&a_{1n}\\ \vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nn} \end{bmatrix}$ 。

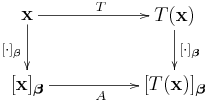
如果以線性變換表示矩陣 $A$ 取代 $T$ ，則 $\mathbf{x}$ 經過 $T$ 映射的像 (image) $T(\mathbf{x})$ 可轉換為矩陣運算 $\displaystyle \begin{bmatrix} T(\mathbf{x}) \end{bmatrix}_{\boldsymbol{\beta}}=A[\mathbf{x}]_{\boldsymbol{\beta}}$ ，見下圖：

線性算子 $T$ 和表示矩陣 $A$ 是同一件事情的兩種表述。我們將線性算子 $T$ 的值域 (image 或 range) 記為 $\text{im}(T)$ 或 $\text{ran}(T)$ ， $T$ 的核 (kernel) 記為 $\ker(T)$ (見“線性變換與矩陣的用語比較”)。因為 $\text{im}(T)$ 和 $\ker(T)$ 是 $\mathcal{V}$ 的子空間，而 $C(A)$ 和 $N(A)$ 是 $\mathbb{R}^n$ 的子空間，「那一個表示矩陣的行空間與零空間和線性變換的值域與核是相同的？」是一個錯誤的問題 (好比一箱蘋果和一籃橘子不相同)。正確的問法是：那一個表示矩陣的行空間與零空間和線性變換的值域與核是同構的？答案是通通有獎。對於 $\mathcal{V}$ 的任意基底 $\boldsymbol{\beta}$ ，座標映射 $[\cdot]_{\boldsymbol{\beta}}$ 是一個同構，由此可知 $\text{im}(T)\cong C(A)$ 且 $\ker(T)\cong N(A)$ 。

如果向量空間 $\mathcal{V}$ 有第二組基底 $\boldsymbol{\gamma}=\{\mathbf{w}_1,\ldots,\mathbf{w}_n\}$ 且

$\displaystyle T(\mathbf{w}_j)=b_{1j}\mathbf{w}_1+\cdots+b_{nj}\mathbf{w}_n,~~j=1,\ldots,n$ ，

則 $T$ 參考 $\boldsymbol{\gamma}$ 的表示矩陣為

$\displaystyle B=[T]_{\boldsymbol{\gamma}}=\begin{bmatrix} b_{11}&\cdots&b_{1n}\\ \vdots&\ddots&\vdots\\ b_{n1}&\cdots&b_{nn} \end{bmatrix}$ 。

同樣地，線性算子 $T$ 參考基底 $\boldsymbol{\gamma}$ 的矩陣實現可用下圖表示：

參考不同基底的表示矩陣 $A$ 和 $B$ 有甚麼關係？寫出兩組基底的映射關係式 (見“圖解基底變換、座標變換、相似變換與相似矩陣”)

$\displaystyle \mathbf{w}_j=\phi(\mathbf{v}_j)=m_{1j}\mathbf{v}_1+\cdots+m_{nj}\mathbf{v}_n,~~~j=1,\ldots,n$ ，

利用上式計算

$\displaystyle \begin{aligned} T(\mathbf{w}_j)&=T\left(\phi(\mathbf{v}_j)\right)=T\left(\sum_{k=1}^nm_{kj}\mathbf{v}_k\right)\\ &=\sum_{k=1}^nm_{kj}T(\mathbf{v}_k)=\sum_{k=1}^nm_{kj}\sum_{i=1}^na_{ik}\mathbf{v}_i\\ &=\sum_{i=1}^n\left(\sum_{k=1}^na_{ik}m_{kj}\right)\mathbf{v}_i.\end{aligned}$

另一方面，從已知的 $T(\mathbf{w}_j)$ 的線性組合表達式出發，亦可得

$\displaystyle\begin{aligned} T(\mathbf{w}_j)&=\sum_{k=1}^nb_{kj}\mathbf{w}_k=\sum_{k=1}^nb_{kj}\phi(\mathbf{v}_k)\\ &=\sum_{k=1}^nb_{kj}\sum_{i=1}^nm_{ik}\mathbf{v}_i=\sum_{i=1}^n\left(\sum_{k=1}^nm_{ik}b_{kj}\right)\mathbf{v}_i. \end{aligned}$

比較兩式的係數，

$\displaystyle \sum_{k=1}^na_{ik}m_{kj}=\sum_{k=1}^nm_{ik}b_{kj},~~~i,j=1,\ldots,n$ 。

令 $M=[m_{ij}]$ 為一個 $n\times n$ 階可逆矩陣 (兩組基底之間的映射必定可逆)。因為 $A=[a_{ij}]$ 且 $B=[b_{ij}]$ ，上式可寫成矩陣形式 $AM=MB$ ，即 $B=M^{-1}AM$ 。這是一個非常重要的結果：兩相似矩陣是某一線性算子參考不同基底的表示矩陣。同構是一種等價關係。因為 $\text{im}(T)\cong C(A)$ 且 $\text{im}(T)\cong C(B)$ ，可知 $C(A)\cong C(B)$ 。同樣道理， $\ker(T)\cong N(A)$ 且 $\ker(T)\cong N(B)$ ，可知 $N(A)\cong N(B)$ 。所以，兩相似矩陣有同構的行空間和零空間。

經過以上討論，「相似家族」的行空間和零空間性質已然梳理清楚。假設 $A$ 和 $B$ 是線性算子 $T:\mathcal{V}\to\mathcal{V}$ 參考不同基底的 $n\times n$ 階表示矩陣， $M$ 是兩組基底變換的表示矩陣，則 $B=M^{-1}AM$ ，且下列性質成立:

純量矩陣僅與其自身相似。若每一 $\mathbf{x}\in\mathcal{V}$ ， $T(\mathbf{x})=c\mathbf{x}$ ，則不論選擇那個基底， $T$ 有唯一的表示矩陣 $cI$ 。
非純量矩陣的「相似家族」包含無窮多個成員。
若 $A$ 是可逆矩陣，則 $A$ 和 $B$ 有相同的行空間 $\mathbb{R}^n$ ，以及相同的零空間 $\{\mathbf{0}\}$ 。
若 $A$ 是不可逆矩陣，則 $A$ 和 $B$ 未必有相同的行空間和零空間，原因是存在可逆矩陣 $M$ 使得 $C(M^{-1}A)\neq C(A)$ 且 $N(AM)\neq N(A)$ 。
線性算子 $T$ 的值域 $\text{im}(T)$ 同構於表示矩陣 $A$ 的行空間 $C(A)$ ，線性算子 $T$ 的核 $\ker(T)$ 同構於表示矩陣 $A$ 的零空間 $N(A)$ 。
對於線性算子 $T$ ，所有的表示矩陣組成的「相似家族」有同構的行空間和零空間。

	陳倍恩 on 線性代數的第一堂課──矩陣乘法的定義
	輕鬆談如何教學二項式定理？… on 牛頓的二項式定理 (上)
	madhouse on 高斯消去法
	WishMobile on 翻轉 LU 分解
	周子傑 on Karush-Kuhn-Tucker (KKT) 條件
	Cloud Huang on 線性泛函與伴隨

答matrix67──關於二相似矩陣的行空間與零空間的關係

Leave a Reply Cancel reply

搜尋(繁體中文或英文)

訊息看板

近期文章

線性代數專欄

其他主題專欄

每週問題

數據充分性問題

其他分類

Recent Comments

近期最多人點閱

分類

Archives

標籤雲

線代線上影音課程

線代學習網站

線代電子書

矩陣計算器

LaTeX

Blogroll

訂閱

閱讀導引

學習資源

專題探究

急救查詢

其他分頁

Meta

網路狀態

Blog Stats

答matrix67──關於二相似矩陣的行空間與零空間的關係

Share this:

Like this:

Leave a Reply Cancel reply

搜尋(繁體中文或英文)

訊息看板

近期文章

線性代數專欄

其他主題專欄

每週問題

數據充分性問題

其他分類

Recent Comments

近期最多人點閱

分類

Archives

標籤雲

線代線上影音課程

線代學習網站

線代電子書

矩陣計算器

LaTeX

Blogroll

訂閱