每週問題 March 11, 2013

這是從矩陣乘積的跡數判斷矩陣性質的問題。

Let $A$ be an $n\times n$ real matrix. Prove the following statements.
(a) If $\mathrm{trace}(AB)=0$ for every $n\times n$ real matrix $B$ , then $A=0$ .
(b) If $\mathrm{trace}(AB)=0$ for every $n\times n$ real matrix $B$ with $\mathrm{trace}B=0$ , then $A=tI$ , where $t$ is any real number.

參考解答：

(a) 使用逆否命題法。假設 $A\neq 0$ ，則 $\mathrm{trace}(AA^T)=\sum_{i=1}^n\sum_{j=1}^na_{ij}^2>0$ ，故證得所求。

(b) 令 $\mathcal{M}_n(\mathbb{R})$ 表示 $n\times n$ 階實矩陣所構成的向量空間， $\dim \mathcal{M}_n(\mathbb{R})=n^2$ 。所有滿足 $\mathrm{trace}B=0$ 的實矩陣 $B$ 構成 $\mathcal{M}_n(\mathbb{R})$ 的一子空間 $\mathcal{X}$ ，理由如下：若 $B, C\in \mathcal{X}$ ， $k\in\mathbb{R}$ ，則 $\mathrm{trace}(B+C)=\mathrm{trace}B+\mathrm{trace}C=0+0=0$ 且 $\mathrm{trace}(kB)=k~\mathrm{trace}B=k\cdot 0=0$ ，故 $\mathrm{trace}(B+C)\in\mathcal{X}$ 且 $\mathrm{trace}(kB)\in\mathcal{X}$ 。子空間 $\mathcal{X}$ 中成員矩陣的唯一限制是主對角元之和等於零，故 $\dim\mathcal{X}=n^2-1$ 。考慮定義於 $\mathcal{M}_n(\mathbb{R})$ 的內積運算:

$\left\langle A,B\right\rangle=\mathrm{trace}(A^TB)$ 。

根據題意，對於任一 $B\in\mathcal{X}$ ， $\mathrm{trace}(AB)=\left\langle A^T,B\right\rangle=0$ ，這說明 $A^T$ 屬於 $\mathcal{X}$ 的正交補餘 (orthogonal complement)，記為 $\mathcal{X}^{\perp}$ 。因為 $\dim\mathcal{X}^{\perp}=1$ 且 $\left\langle I,B\right\rangle=\mathrm{trace}(IB)=\mathrm{trace}B=0$ ，可知 $\mathcal{X}^{\perp}$ 由單位矩陣 $I$ 擴張而成。所以， $A=tI$ ，其中 $t$ 是任一實數。

PowSol-March-11-13

2 Responses to 每週問題 March 11, 2013

12345 says:

03/11/2013 at 10:21 am

於問題(b)中，子空間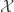 $\mathcal{X}$ 的維度要怎麼算呢?

- ccjou says:
  
  03/11/2013 at 10:31 am
  
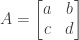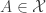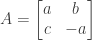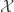  以二階方陣為例，令 $A=\begin{bmatrix} a&b\\ c&d \end{bmatrix}$ 。顯然， $\dim\mathcal{M}_2=2^2=4$ 。若 $A\in\mathcal{X}$ ，則 $\mathrm{trace}A=a+d=0$ ，故 $A$ 可表示為 $A=\begin{bmatrix} a&b\\ c&-a \end{bmatrix}$ ，也就是說， $\begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix},\begin{bmatrix} 0&1\\ 0&0 \end{bmatrix},\begin{bmatrix} 0&0\\ 1&0 \end{bmatrix}$ 構成 $\mathcal{X}$ 的一組基底，所以 $\dim\mathcal{X}=4-1=3$ 。運用類似方法可推廣至 $n>2$ 的情形。

	陳倍恩 on 線性代數的第一堂課──矩陣乘法的定義
	輕鬆談如何教學二項式定理？… on 牛頓的二項式定理 (上)
	madhouse on 高斯消去法
	WishMobile on 翻轉 LU 分解
	周子傑 on Karush-Kuhn-Tucker (KKT) 條件
	Cloud Huang on 線性泛函與伴隨