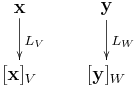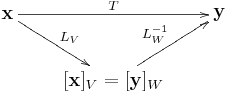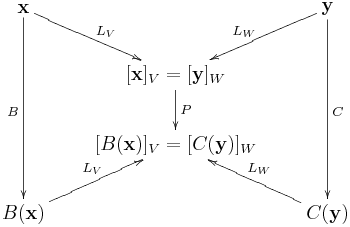本文的閱讀等級:中級
在線性變換中,最令學者困惑的主題莫過於揉合了基底、座標、線性變換與其表示矩陣的變換問題。令 為一個定義於
的向量空間,
。設
和
是向量空間
的兩組基底。以下是四個典型的變換問題[1]。
Q1 基底變換:若 ,
且
,向量
和
有甚麼關係?
Q2 座標變換:若 ,
,座標
和
有甚麼關係?
Q3 相似變換:若 且
,
,線性變換
和
有甚麼關係?
Q4 相似矩陣:若 且
,
,矩陣
和
有甚麼關係?
解決這四個變換問題的預備知識包括線性變換基本性質、座標映射和線性變換表示矩陣,簡述於下。
(1) 線性變換基本性質:若 為一個線性變換 (或稱線性算子),則對於
,和純量
,
(2) 座標映射:對於任一 ,存在唯一的有序數組
使得
。
我們說 是向量
參考基底
的座標向量,兩者之間具有一對一相映關係 (見“啊哈!原來變換矩陣這麼簡單”):
若線性變換 使得
,則
稱為基底
的座標映射。因為
和
是同構的向量空間 (見“同構的向量空間”),
是可逆映射,就有
。
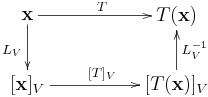
(3) 線性變換表示矩陣:我們定義線性變換 參考基底
的
階表示矩陣為 (見“線性變換表示矩陣”)
,
滿足 。因為
(這裡
代表複合變換
) 且
,推知
。由於
是任意向量,定有
。
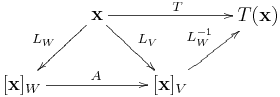
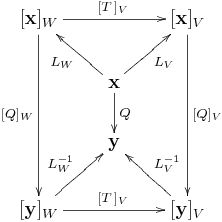
上式左乘或右乘 ,可得
或
,圖示如下:
以下每一個變換問題都提供兩個解法。第一個解法使用線性組合 (向量加法和純量乘法) 搭配線性變換基本性質運算;第二個解法採用座標映射和線性變換表示矩陣的複合運算 (矩陣乘法),並借助對等的映射圖推論。
Q1 基底變換
若 ,
向量 和
有甚麼關係?
解法A:換一個問法,從向量 如何映至
?關鍵在於聯繫兩組基底的線性變換。設
為一個線性變換,滿足
,
,則
所以,從 映至
的線性變換
正是將有序基底
映至另一組有序基底
的基底變換。
解法B:我們從座標映射觀點來回答這個問題。令 表示向量
參考基底
的座標向量,
表示向量
參考基底
的座標向量。設
和
代表座標映射,分別滿足
和
,圖示如下:
由已知條件 可得
,故
。
令 。因為
是任意向量,即知
。以上推論過程可以轉換成圖形描述:將
加入上圖,黏合
和
,反轉
的箭頭方向 (對應的線性映射改成
),就有
圖中顯示兩條從 映至
的等價路徑,推知
。
為保險起見,我們還要驗證解法A和解法B有相同的結果,也就是說, 確實是將
映至
的基底變換。因為
,
代表
的標準單位向量 (第
元等於
,其餘元等於
)。同樣地,
,所以
。
Q2 座標變換
若 ,
,
座標向量 和
有甚麼關係?
解法A:Q1與Q2的主要差異在於前者求線性變換而後者問矩陣。將問題改為:從座標向量 映至
的座標變換矩陣為何?(當然我們也可以考慮從
映至
的座標變換矩陣,兩者互為逆矩陣。) 注意,
不僅是
經基底變換
映射得到的像 (image),同時也可唯一表示成
的線性組合,如下:
。
將上式代入 以
組合的表達式,
比較上式和 的係數,立得
,
或改寫成矩陣形式
,
其中 即為基底變換
參考
的表示矩陣
,因為
。
我們得到了一個令人訝異的結果:座標變換矩陣 正是基底變換
參考
的表示矩陣 (相關討論見“座標變換與基底變換的對應關係”)。何以
和
的映射方向相反?從座標映射的角度很容易解釋這個現象。
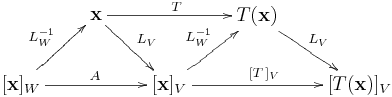
解法B:採用座標映射可以大大簡化推導過程。Q2其實在問滿足下圖的座標變換矩陣 為何?
從上圖映射路徑 (反轉 ),立知
,或直接計算得到
。
根據Q1解法B,,從映射圖如何推論
?也就是說,如何推得
?上圖中加入
和
(因為
),即有
基底變換 參考
的表示矩陣
滿足
或
,故上圖可擴充如下:
圖中, 和
有相同的等價映射路徑
,因此證明
。注意,上半部的
定義於向量空間
,下半部的
(即
) 定義於
,而
和
提供從
至
的映射。
Q3 相似變換
若對於 ,
線性變換 和
有甚麼關係?
解法A:同Q1和Q2的解法A,我們使用線性組合與線性變換基本性質運算。因為基底變換 滿足
,
,可知
。
另外,套用給出條件,
。
合併上面兩式,即有
,
可知對於任一 ,
,故
。因為
是可逆變換,左乘或右乘
可得
或
,我們稱線性變換
相似於
(見“相似變換下的不變性”)。
解法B:令 ,由給出條件可知
即為線性變換
參考
的表示矩陣
,同樣也是線性變換
參考
的表示矩陣
。將關係式
,
,
彙整成下圖:
圖中 的兩條等價映射路徑指出
,同時左乘
,右乘
,可得
(分別對應從
至
沿著下緣和上緣的映射路徑)。因為
,故得
。上圖加入
,
,完整的相似變換映射圖如下:
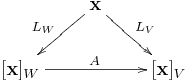
Q4 相似矩陣
若 為一個線性變換,對於
,
線性變換表示矩陣 和
有甚麼關係?
解法A:寫出Q2解法A的基底變換 表達式
,
用它來計算
另一方面,從已知的 的線性組合表達式出發,亦可得
比較兩式的係數,
。
因為 ,
和
,上式可寫成矩陣形式
,
左乘或右乘 ,可得
。
因此,線性變換 參考
的表示矩陣
相似於
參考
的表示矩陣
。
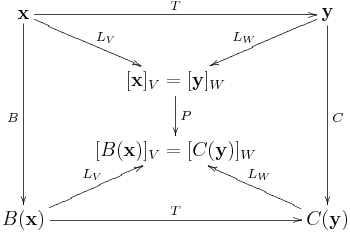
解法B:類似Q3解法B,線性變換 與其表示矩陣
和
具有下列關係:
和
,合併可得
。上式左乘
,右乘
,就有
。因為
,故
。從下面的相似矩陣的映射圖也可以立刻推得相同結論。
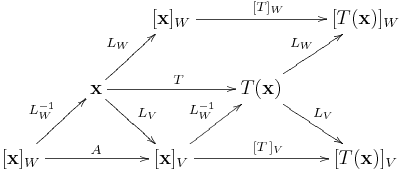
結語:映射圖是處理線性變換問題的一種形象化方法,直觀地表示基底變換、座標映射與其他線性變換的交互作用。圖中的頂點可以是向量或座標向量,有向邊代表線性變換 (含基底變換和座標映射) 或線性變換表示矩陣。映射圖的設計程序大致如下:根據題意挑選出重要的頂點和有向邊,以適當符號標記,接著透過頂點之間的串聯繪出有向邊,必要時再修改補添頂點和有向邊至完成全圖為止。不過,如果給定的是數值應用問題,即便圖解法能迅速導出關鍵公式,必要的計算仍不可免。他日將針對數值問題另文舉例說明圖解法的實際操作。
後註1:本文介紹的線性算子 變換問題解法可推廣至一般線性變換
,即定義域
和到達域
是不同的向量空間。細部工作就留給讀者自行完成。
後註2:Q2說明了座標變換矩陣 (滿足
) 等於基底變換
參考
的表示矩陣
。事實上,
也等於基底變換
參考
的表示矩陣
,也就是說,
。若採用解法A,寫出
的組合表達式
,
則
,
故知
,
因此證明 。若採用解法B,擴充Q2解法B的映射圖如下:
比較從左下 至右上
的兩條等價映射路徑:
立得 。
參考來源:
[1] Paul R. Halmos, Finite-Dimensional Vector Spaces, Springer, 1958, pp 82-84.