仿射組合與仿射空間

Posted on 09/24/2012 by ccjou

本文的閱讀等級：初級

考慮線性方程 $A\mathbf{x}=\mathbf{b}$ ，所有可能的解稱為通解，具有下列形式：

$\mathbf{x}=\mathbf{x}_p+\mathbf{x}_h$ ，

其中特解 $\mathbf{x}_p$ 是指滿足 $A\mathbf{x}_p=\mathbf{b}$ 的任一解，齊次解 $\mathbf{x}_h$ 則滿足 $A\mathbf{x}_h=\mathbf{0}$ 。除非齊次解僅包含平凡解 $\mathbf{0}$ ，否則特解和齊次解皆不唯一，故通解有無窮多種表達式。見下例：

$\begin{bmatrix} 1&2&4\\ 1&3&5 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 4\\ 5 \end{bmatrix}$

的通解可以表示為

$\mathbf{x}=\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}+\alpha\left[\!\!\begin{array}{r} 2\\ 1\\ -1 \end{array}\!\!\right]=\left(\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}+\beta\left[\!\!\begin{array}{r} 2\\ 1\\ -1 \end{array}\!\!\right]\right)+\gamma\left[\!\!\begin{array}{r} 2\\ 1\\ -1 \end{array}\!\!\right]$ ，

上式中， $\alpha, \beta, \gamma$ 是任意實數，改變 $\beta$ 數值即產生新的特解 $\mathbf{x}_p=\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}+\beta\left[\!\!\begin{array}{r} 2\\ 1\\ -1 \end{array}\!\!\right]$ ，齊次解則為 $\mathbf{x}_h=\gamma\left[\!\!\begin{array}{r} 2\\ 1\\ -1 \end{array}\!\!\right]$ 。幾何空間向量可用其端點表示，上例通解 (即所有特解構成的集合) 是 $\mathbb{R}^3$ 中一不穿越原點的直線，故不為子空間 (任一子空間必定包含原點)。另一方面，所有的齊次解都位於穿越原點的平行直線上，此即 $A$ 的零空間 (見“Ax=b 和 Ax=0 的解集合有什麼關係？”)。所以，通解與齊次解之間具有點對點的平移關係，而該平移量可以是任一滿足線性方程的特解 $\mathbf{x}_p$ 。通解、特解和齊次解之間的關係常令學者感到困惑，本文介紹兩個新概念──仿射組合與仿射空間，希望藉此得以釐清特解和齊次解的幾何意義。

仿射組合 (affine combination) 是一種特殊的線性組合。給定向量 $\mathbf{v}_1,\ldots,\mathbf{v}_k\in\mathbb{R}^n$ ，它們的仿射組合定義為

$c_1\mathbf{v}_1+\cdots+c_k\mathbf{v}_k$ ，

其中組合權重 $c_1,\ldots,c_k$ 滿足 $c_1+\cdots+c_k=1$ 。仿造擴張的概念，仿射擴張 (affine span) 是 $\mathbf{v}_1,\ldots,\mathbf{v}_k$ 的所有仿射組合形成的集合，記為 $\mathrm{aff}\{\mathbf{v}_1,\ldots,\mathbf{v}_k\}$ 。在不造成混淆的情況下，一幾何空間向量可以視為一點座標。對於向量 $\mathbf{v}_1$ ， $\mathrm{aff}\{\mathbf{v}_1\}$ 僅包含該點，因為仿射組合的形式是 $c_1\mathbf{v}_1$ 且 $c_1=1$ 。若 $\mathbf{v}_1$ 和 $\mathbf{v}_2$ 為二相異點，考慮 $\mathbf{x}=c_1\mathbf{v}_1+c_2\mathbf{v}_2$ ，其中 $c_1+c_2=1$ 。令 $t=c_2$ ，則 $c_1=1-c_2=1-t$ ，就有

$\mathbf{x}=(1-t)\mathbf{v}_1+t\mathbf{v}_2$ ，

此即我們熟悉的直線參數式，代表穿越 $\mathbf{v}_1$ (當 $t=0$ ) 和 $\mathbf{v}_2$ (當 $t=1$ ) 的直線。將上式改寫為

$\mathbf{x}=\mathbf{v}_1+t(\mathbf{v}_2-\mathbf{v}_1)=\mathbf{p}+t\mathbf{u}$ ，

其中 $\mathbf{p}=\mathbf{v}_1$ 且 $\mathbf{u}=\mathbf{v}_2-\mathbf{v}_1$ 。見下圖， $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2\}$ 等於 $\mathrm{span}\{\mathbf{u}\}$ 加上 $\mathbf{p}$ ，也就是穿越 $\mathbf{u}$ 和原點的直線上每一點經過平移 $\mathbf{p}$ 後的平行直線。如果 $\mathbf{v}_1=\mathbf{v}_2$ ，則 $\mathbf{u}=\mathbf{0}$ ，這時 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2\}$ 退化為一點 $\mathbf{v}_1$ 。

仿射擴張 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2\}$

仿射組合的表達式還可以改寫為 $\mathbf{x}-\mathbf{v}_1=t(\mathbf{v}_2-\mathbf{v}_1)$ ，意思是對於仿射擴張 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2\}$ 中任一向量 $\mathbf{x}$ ， $\mathbf{x}-\mathbf{v}_1$ 皆可寫成 $\mathbf{v}_2-\mathbf{v}_1$ 的線性組合。下面的定理將此性質推廣至一般情況。

定理一：若 $\mathbf{x}\in\mathrm{aff}\{\mathbf{v}_1,\ldots,\mathbf{v}_k\}$ ，則 $\mathbf{x}-\mathbf{v}_1$ 必可以表示成 $\mathbf{v}_2-\mathbf{v}_1,\ldots,\mathbf{v}_k-\mathbf{v}_1$ 的線性組合，反之亦然。

證明於下。若

$\mathbf{x}=c_1\mathbf{v}_1+\cdots+c_k\mathbf{v}_k$ ，

其中 $c_1+\cdots+c_k=1$ ，則 $c_1=1-c_2-\cdots-c_k$ ，代入上式，

$\begin{aligned} \mathbf{x}&=(1-c_2-\cdots-c_k)\mathbf{v}_1+c_2\mathbf{v}_2+\cdots+c_k\mathbf{v}_k\\ &=\mathbf{v}_1+c_2(\mathbf{v}_2-\mathbf{v}_1)+\cdots+c_k(\mathbf{v}_k-\mathbf{v}_1), \end{aligned}$

立得

$\mathbf{x}-\mathbf{v}_1=c_2(\mathbf{v}_2-\mathbf{v}_1)+\cdots+c_k(\mathbf{v}_k-\mathbf{v}_1)$ 。

明顯地，相反方向的推論也成立。

考慮 $\mathbb{R}^n$ 中不共線的三相異點 $\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3$ ，利用定理一很容易確認 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$ 的幾何型態。對於 $\mathbf{x}\in\mathrm{aff}\{\mathbf{x}_1,\mathbf{v}_2,\mathbf{v}_3\}$ ，必定存在 $c_2$ 和 $c_3$ ，使得 $\mathbf{x}-\mathbf{v}_1=c_2(\mathbf{v}_2-\mathbf{v}_1)+c_3(\mathbf{v}_3-\mathbf{v}_1)$ ，也就有

$\mathbf{x}=\mathbf{v}_1+c_2(\mathbf{v}_2-\mathbf{v}_1)+c_3(\mathbf{v}_3-\mathbf{v}_1)$ 。

上式指出 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$ 即為 $\mathrm{span}\{\mathbf{v}_2-\mathbf{v}_1,\mathbf{v}_3-\mathbf{v}_1\}$ 平移 $\mathbf{v}_1$ 而得的平面，也就是穿越 $\mathbf{v}_1,\mathbf{v}_2$ 和 $\mathbf{v}_3$ 的平面，見下圖。

仿射擴張 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$

接下來我用一個例子說明如何利用定理一判別給定向量是否屬於仿射擴張。令

$\mathbf{v}_1=\begin{bmatrix} 4\\ 0\\ 1 \end{bmatrix},~\mathbf{v}_2=\begin{bmatrix} 2\\ 3\\ 5 \end{bmatrix},~\mathbf{v}_3=\begin{bmatrix} 1\\ 4\\ 2 \end{bmatrix},~\mathbf{x}=\begin{bmatrix} 3\\ 2\\ 8 \end{bmatrix}~\mathbf{y}=\begin{bmatrix} 3\\ 3\\ 0 \end{bmatrix}$ 。

如果 $\mathbf{x}$ (或 $\mathbf{y}$ ) 落在穿越 $\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3$ 的平面上，則 $\mathbf{x}-\mathbf{v}_1$ (或 $\mathbf{y}-\mathbf{v}_1$ ) 可表示為 $\mathbf{v}_2-\mathbf{v}_1$ 和 $\mathbf{v}_3-\mathbf{v}_1$ 的線性組合。寫出增廣矩陣 $\begin{bmatrix} \mathbf{v}_2-\mathbf{v}_1&\mathbf{v}_3-\mathbf{v}_1&\vert&\mathbf{x}-\mathbf{v}_1&\mathbf{y}-\mathbf{v}_1 \end{bmatrix}$ ，化簡至簡約列梯形式，如下：

$\left[\!\!\begin{array}{rrcrr} -2&-3&\vline&-1&-1\\ 3&4&\vline&2&3\\ 4&1&\vline&7&-1 \end{array}\!\!\right]\to\left[\!\!\begin{array}{cccrc} 1&0&\vline&2&0\\ 0&1&\vline&-1&0\\ 0&0&\vline&0&1 \end{array}\!\!\right]$ 。

由簡約列梯形式的第三行係數可知 (見“由簡約列梯形式判斷行空間基底”)

$\mathbf{x}-\mathbf{v}_1=2(\mathbf{v}_2-\mathbf{v}_1)-(\mathbf{v}_3-\mathbf{v}_1)$ ，

故 $\mathbf{x}$ 屬於平面 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$ 。由第四行係數可推論 $\mathbf{y}-\mathbf{v}_1$ 無法表示為 $\mathbf{v}_2-\mathbf{v}_1$ 和 $\mathbf{v}_3-\mathbf{v}_1$ 的線性組合，也就是說 $\mathbf{y}$ 不屬於 $\mathrm{aff}\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}$ 。

從以上討論可知仿射擴張的幾何意義是「一個子空間加上平移」，因為這個緣故，我們稱 $\mathbb{R}^n$ 的子空間 $\mathcal{W}$ 自原點平移 $\mathbf{p}\in\mathbb{R}^n$ 後所構成的集合 $\mathcal{S}$ 為仿射空間 (affine space)，記作

$\mathcal{S}=\mathcal{W}+\mathbf{p}\overset{\underset{\mathrm{def}}{}}{=}\{\mathbf{w}+\mathbf{p}\vert\mathbf{w}\in\mathcal{W}\}$ 。

我們定義仿射空間 $\mathcal{S}$ 的維數等於子空間 $\mathcal{W}$ 的維數，記為 $\dim\mathcal{S}=\dim\mathcal{W}$ 。定理二宣告仿射擴張就是仿射空間。

定理二：對於 $\mathbf{v}_1,\ldots,\mathbf{v}_k\in\mathbb{R}^n$ ，若 $\mathcal{S}=\mathrm{aff}\{\mathbf{v}_1,\ldots,\mathbf{v}_k\}$ ，則 $\mathbb{R}^n$ 中存在一個子空間 $\mathcal{W}$ 與點 $\mathbf{p}\in\mathcal{S}$ ，使得 $\mathcal{S}=\mathcal{W}+\mathbf{p}$ 。

證明過程類似定理一。對於任一 $\mathbf{x}\in\mathcal{S}$ ，必存在 $c_1+\cdots+c_k=1$ 使得

$\begin{aligned} \mathbf{x}&=c_1\mathbf{v}_1+\cdots+c_k\mathbf{v}_k\\ &=(1-c_2-\cdots-c_k)\mathbf{v}_1+c_2\mathbf{v}_2+\cdots+c_k\mathbf{v}_k\\ &=\mathbf{v}_1+c_2(\mathbf{v}_2-\mathbf{v}_1)+\cdots+c_k(\mathbf{v}_k-\mathbf{v}_1), \end{aligned}$

其中 $c_2,\ldots,c_k$ 是任意實數。令 $\mathcal{W}=\mathrm{span}\{\mathbf{v}_2-\mathbf{v}_1,\ldots,\mathbf{v}_k-\mathbf{v}_1\}$ ， $\mathbf{p}=\mathbf{v}_1$ ，立知 $\mathcal{S}\subseteq\mathcal{W}+\mathbf{p}$ 。反過來推論亦可得到 $\mathcal{W}+\mathbf{p}\subseteq\mathcal{S}$ ，因此證明 $\mathcal{S}=\mathcal{W}+\mathbf{p}$ 。

相反的，給定一仿射空間 $\mathcal{S}=\mathcal{W}+\mathbf{p}$ ，其中 $\mathcal{W}=\mathrm{span}\{\mathbf{w}_1,\ldots,\mathbf{w}_k\}$ ，運用相同方法也可以推論 $\mathcal{S}$ 的仿射擴張表達式為 $\mathcal{S}=\mathrm{aff}\{\mathbf{p},\mathbf{w}_1+\mathbf{p},\ldots,\mathbf{w}_k+\mathbf{p}\}$ 。最後特別強調：平移量 $\mathbf{p}$ 可為仿射空間 $\mathcal{S}$ 中任一向量，換句話說，不論任何 $\mathbf{p},\mathbf{q}\in\mathcal{S}$ ，都有 $\mathcal{W}+\mathbf{p}=\mathcal{W}+\mathbf{q}$ 。這個證明工作就留給讀者自行完成。

This entry was posted in 線性代數專欄, 仿射幾何 and tagged 特解, 通解, 仿射空間, 仿射組合. Bookmark the permalink.

14 Responses to 仿射組合與仿射空間

延伸寸 says:

10/14/2012 at 1:19 pm

本文意猶未竟。要如何利用文中的定理來解答下列 link 的第一題呢？

Click to access 982131.pdf

我覺得這一題出得很好。計算不難但若觀念不全通(我就是)的同學解起來會很困難。我甚至建議周老師為本題寫一篇通脈文。

Reply
- ccjou says:
  
  10/14/2012 at 10:19 pm
  
  確實是一個有趣的問題，我要想一想該怎麼回答。
  
  Reply
  - 張盛東 says:
    
    08/29/2013 at 12:46 pm
    
    老師，關於這一題我有一個思路。因為無論是哪一種形式的general solution，表示零空間的超平面都不變，所以可以根據第一個general solution中已知的兩個零空間的基向量求出超平面的法向量，然後根據這個法向量與第二個general solution的兩個基向量的內積為零得到beta和gamma，最後由平移向量在法向量方向的分量相等求出alpha。不知這個思路是否正確？
    
    Reply
    - ccjou says:
      
      08/29/2013 at 2:27 pm
      
      你真是有心向學啊。這個思路是正確的，請參閱
      
      答延伸寸──關於線性方程的通解表達
      
      Reply
      - 張盛東 says:
        
        08/29/2013 at 10:35 pm
        
        這多虧老師的網站激發起了我的學習動力。沒有老師的網站我就不會知道線代是如此的簡潔和精妙。
        
        原來老師已經為這一個問題寫了解答文。
        
        Reply
ccjou says:

08/30/2013 at 1:16 pm

這個網站激發起了學習動力？聽聽看另一種觀點。2012年8月紐約時報：學習代數有必要嗎？作者Andrew Hacker是紐約城市大學皇后學院的一名政治科學教授。
http://cn.nytimes.com/opinion/20120808/c08algebra/dual/

我將第一段和最後一段(通常是最精華的部分)抄寫下來：

在美國的學校，每天約有600萬名高中生和200萬名大一新生在與代數作鬥爭。不管是在高中還是大學，都會有大量學生代數考試不及格。我們為什麼要讓美國學生受這樣的折磨？我發現自己越來越強烈地認為，我們不應該這麼做。

……

是的，不管他們願意與否，年輕人都應該學習如何讀寫，如何做長除法。但是，我們沒有理由強迫他們掌握向量夾角和非連續函數。我們把數學當作一塊巨石，讓大家都使勁推，卻不去評估這一切痛苦會帶來什麼成果。那麼，我們為什麼要求每個人都學那麼多數學，卻沒有替代課程或例外安排？迄今我還沒找到一個令人信服的答案。

Reply
- 張盛東 says:
  
  08/31/2013 at 11:36 am
  
  老師，這該怎麼說呢。我的觀點是，要令人對某一學科產生興趣，必須先讓這個人體會到這一學科的價值。然而，能最快做到這一點的方法，就是讓這個人不斷嘗試用該學科來解決生活中的問題。學校中關於代數的教學，有時候的確過分強調方法，忽略實際，猶如教學生屠龍之術，打擊了學生的積極性。現在美國不少大學採用的線代教材採用的知識點引入方式就是先提出實際問題，然後用線代建模，最後介紹線代理論解決問題，例如Gilbert Strang的Introduction to Linear Algebra，我覺得這是一個不錯的進步。儘管課時的限制下會造成課程深度的不足，但作為入門課程已經足夠了，起碼會激起某些學生繼續學習的興趣，我覺得這已經是一種成功。
  
  而且，抽象的學科，如數學，邏輯，和哲學，本來就不是面向大眾的學科。所以我認為學校可以做的，就是因材施教，不同專業的學生要上不同難度的數學。原因是，讀不同專業的學生必然會以自身專業的思維方式思考問題，一下子讓來自各個系的學生都以數學系學生的思維方式解決數學問題，本身就是揠苗助長。所以我覺得老師提供的這篇文章作者的觀點有可取之處，但未免有些武斷。
  
  Reply
  - ccjou says:
    
    08/31/2013 at 5:46 pm
    
    謝謝你提供這麼有見地的論點。數學教育的話語權向來掌握在教學者手上，學習者要嘛概括承受，不然只能消極抵抗。關於這個問題，我相信每一個人都有他自己的看法。Hacker的文章刊登一個月後，一位來自中國大陸目前在美國工作的數學博士也在紐約時報回應「什麼是理想的數學教育」。
    http://cn.nytimes.com/china/20120914/cc14math/zh-hant/
    
    他提出了這樣的問題：在一個一切社會信息都以量化方式表述和處理，一切職業都需要敏銳的判斷力和定量洞察力，一切公眾話題（無論是金融還是醫療，食品安全還是氣候變化）都必須在紮實的數據分析的基礎上才能夠得以有效討論的世界上，一個平均水平的孩子應當為此做好怎樣的智識上的準備和訓練？怎樣才能讓他以一位普通公民的身份走入社會之後，不把自己在校園中接受的數學教育當成某種痛苦的回憶急切地丟在腦海深處，而是充滿信心地繼續成人學習，以適應這個飛速變化的數字時代？
    
    說實話，我還蠻慶幸自已在14歲時沒有因為 $x^6-y^6$ 的因式分解而失去對數學的好奇。
    
    Reply
monne says:

05/30/2015 at 3:29 pm

老师，您好，我有个疑问想请老师解答下。我可以认为以下想法成立吗？
若已知S＝W+p，S为仿射空间，W是向量空间（子空间），则，S与W是一一对应关系。当然，这里p属于S，可以任意。也就是说，在定理2中，结论部分，可以写为，存在唯一的向量空间W，与任意属于S的p。
谢谢老师！～

Reply
- ccjou says:
  
  05/30/2015 at 4:09 pm
  
  是的，仿射空間對應唯一的向量空間。若仿射空間 $S=W_1+p=W_2+p$ ，不難證明 $W_1\subseteq W_2$ ，再根據對稱性， $W_2\subseteq W_1$ ，故 $W_1=W_2$ 。
  
  Reply
wonderlandtommy says:

06/13/2016 at 5:00 pm

版主好,
仿射空間的另一個定義:
1.給定任意兩個不同的點，恰有一條線重合兩個點。
2.給定任意直線 l 及任意不與 l 重合的點 P，恰有一條與 P 重合，且不與 l 相交的線。
3.存在4個點，使得沒有線能重合兩個以上的這些點。

請問如何將這個定義與子空間W的平移搭上關係，謝謝版主.

Reply
- ccjou says:
  
  06/14/2016 at 5:51 am
  
  你可以先將這個「定義」改成向量空間語言，再看要如何推論或證明。譬如，給定任意兩個不同的點，恰有一條線重合兩個點=>給定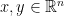 $x,y\in\mathbb{R}^n$ ， $x\neq y$ ，存在唯一仿射空間 $S=W+p$ 使得 $x,y\in S$ 且 $\dim W=1$ 。
  
  Reply
  - wonderlandtommy says:
    
    06/14/2016 at 5:35 pm
    
    也許在n維Euclidean space下,”直線”暗指n-1維超平面。
    
    Reply
Pingback: 向量空间和子空间 – Bruno的个人博客

	xmj on 內積的定義
	Ning ChingSan on 線性代數的第一堂課──矩陣乘法的定義
	momo on 兩岸線性代數用詞參照
	訪客 on 克拉瑪公式的簡易幾何證明
	悟 on 條件機率與貝氏定理
	jeremy on 內積與外積是怎麼來的？