凸組合、凸包與凸集

Posted on 05/09/2013 by ccjou

本文的閱讀等級：初級

幾何座標空間 \mathbb{R}^n 的一個向量 \mathbf{x}=(x_1,\ldots,x_n) 表示該向量端點的座標。點與座標向量具有一對一的對應關係，因為這個緣故，我們經常以座標向量代表點。本文介紹一種別於子空間與仿射空間 (子空間的平移) 的向量集。我們稱一個向量集 S\subset\mathbb{R}^n 是凸集 (convex set)，若給定任兩點 \mathbf{x},\mathbf{y}\in S 和 0<\alpha<1，點 \alpha\mathbf{x}+(1-\alpha)\mathbf{y} 屬於 S。淺白地說，在凸集中，任兩個點皆可「看見」彼此，連接這兩點的直線段不含集合以外的點。見圖一的例子。比較特別的是，\mathbb{R}^n 所包含的子空間與仿射空間都是凸集。

Convex Sets 2

圖一 凸集與非凸集

 
下面是凸集的基本定理，它說明純量乘法、向量加法和交集運算保留凸性 (convexity)。

 
定理一：對於 \mathbb{R}^n 裏的凸集，下列性質成立：

  1. 若 S 是一個凸集且 c 是實數，則 cS\equiv\{c\mathbf{x}\vert c\in\mathbb{R},~\mathbf{x}\in S\} 是一個凸集。
  2. 若 S 和 T 是凸集，則 S+T\equiv\{\mathbf{x}+\mathbf{y}\vert\mathbf{x}\in S,~\mathbf{y}\in T\} 是一個凸集。
  3. 若 S 與 T 是凸集，則 S\cap T 是一個凸集。

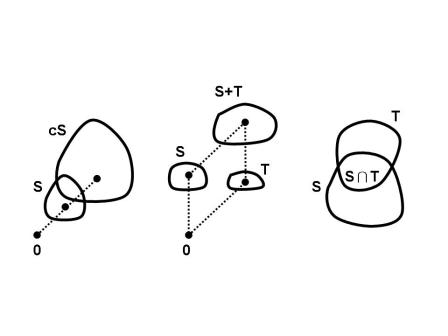
使用定義即可證明。這裡僅提供 (3) 的證明，(1) 和 (2) 留給讀者自行完成。設 \mathbf{x},\mathbf{y}\in S\cap T 且 0< \alpha< 1，可知 \mathbf{x},\mathbf{y} 屬於 S 與 T。因為 S 和 T 是凸集，\alpha\mathbf{x}+(1-\alpha)\mathbf{y} 同時屬於 S 與 T，也就有 \alpha\mathbf{x}+(1-\alpha)\mathbf{y}\in S\cap T，證明 S\cap T 是一個凸集。圖二顯示這三個凸集性質。

Convex Sets 4

圖二 凸集的三個性質

 
考慮幾何座標空間 \mathbb{R}^n 中 k 個點 \mathbf{v}_1,\ldots,\mathbf{v}_k。我們定義 \mathbf{v}_1,\ldots,\mathbf{v}_k 的凸組合 (convex combination) 為

\mathbf{x}=c_1\mathbf{v}_1+\cdots+c_k\mathbf{v}_k，

其中 c_1+\cdots+c_k=1 且每一 c_i\ge 0。凸組合是在線性組合的基礎下，加入係數和等於 1，並限定係數不為負值。以 \mathbb{R}^3 的兩個線性獨立向量 \mathbf{v}_1 和 \mathbf{v}_2 為例，所有的線性組合 c_1\mathbf{v}_1+c_2\mathbf{v}_2 構成一個穿越原點且包含 \mathbf{v}_1 和 \mathbf{v}_2 的平面。如果限制 c_1+c_2=1，則稱為仿射組合；所有的仿射組合構成穿越 \mathbf{v}_1 和 \mathbf{v}_2 的直線 (見“仿射組合與仿射空間”)。再加入 c_1\ge 0 和 c_2\ge 0，即為凸組合；所有的凸組合構成連接 \mathbf{v}_1 和 \mathbf{v}_2 的直線段。對於一個向量集 S，凸包 (convex hull) 是指 S 所含向量的所有凸組合形成的集合，記作 \hbox{conv}(S)。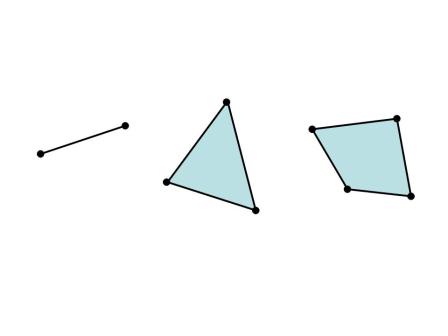明顯地，單一點 S=\{\mathbf{v}_1\} 的凸包為向量本身。圖三顯示 \mathbb{R}^2 平面上兩點、三點和四點產生的凸包。

Convex Sets 1

圖三 平面上由兩點、三點和四點產生的凸包

 
凸包 \hbox{conv}(S) 是一個凸集嗎？是的。凸包 \hbox{conv}(S) 由向量集 S 構成，可知 S\subseteq\hbox{conv}(S)。定理二說明：若 \hbox{conv}(S)\subseteq S，則 S 是一個凸集。因為 \hbox{conv}(S) 的凸包為其自身，故可推論 \hbox{conv}(S) 是一個凸集。

 
定理二：若 S 中任何點的凸組合都屬於 S，即 \hbox{conv}(S)\subseteq S，則 S 是一個凸集；相反陳述亦成立。

我們用數學歸納法來證明。令 m 表示從 S 選取的點數。當 m=1，顯然該點是一個凸集。當 m=2，兩點連成的直線段為一個凸集。假設當 m=k>2 時，命題成立。考慮 \mathbf{y}=c_1\mathbf{v}_1+\cdots+c_k\mathbf{v}_k+c_{k+1}\mathbf{v}_{k+1}，其中 c_1+\cdots+c_{k+1}=1 且所有 0\le c_i\le 1。分開兩個情況討論。若 c_{k+1}=1，則 \mathbf{y}=\mathbf{v}_{k+1} 屬於 S，這時 m=1，命題成立。若 c_{k+1}<1，令 \alpha=c_1+\cdots+c_k。因此 \alpha=1-c_{k+1}>0，就有

\displaystyle \mathbf{y}=(1-c_{k+1})\left(\frac{c_1}{\alpha}\mathbf{v}_1+\cdots+\frac{c_k}{\alpha}\mathbf{v}_k\right)+c_{k+1}\mathbf{v}_{k+1}。

因為 \sum_{i=1}^kc_i/\alpha=1 且每一 c_i/\alpha\ge 0，由歸納假設可知 \mathbf{x}=(c_1/\alpha)\mathbf{v}_1+\cdots+(c_k/\alpha)\mathbf{v}_k 屬於 S，且 \mathbf{y} 是 \mathbf{x} 和 \mathbf{v}_{k+1} 的凸組合，這時 m=2，命題成立。

 
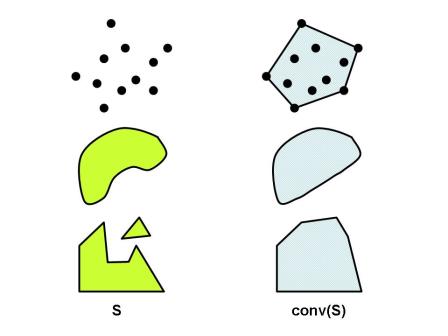
給定一個向量集 S，凸包 \hbox{conv}(S) 有甚麼直觀意義呢？從幾何面來看，凸包 \hbox{conv}(S) 是包含 S 的「最小」凸集 (見定理三)。圖四描繪平面上的向量集 S 與對應的凸包 \hbox{conv}(S)。

Convex Sets 3

圖四 向量集S與凸包conv(S)

 
定理三：對於任意向量集 S，凸包 \hbox{conv}(S) 等於包含 S 的所有凸集的交集。

令 T 表示包含 S 的所有凸集的交集。定理一 (3) 指出 T 是一個凸集。因為 \hbox{conv}(S) 是一個凸集且 S\subseteq\hbox{conv}(S)，可知 T\subseteq \hbox{conv}(S)。另一方面，T 包含 S 推得 \hbox{conv}(S)\subseteq\hbox{conv}(T)。因為 T 是一個凸集，定理二說明 \hbox{conv}(T)=T，故 \hbox{conv}(S)\subseteq T。合併以上結果即證明 \hbox{conv}(S)=T。

 
若 \mathbf{x} 屬於凸包 \hbox{conv}(S)，那麼 \mathbf{x} 可以寫成 S 中某些點的凸組合。但需要多少個點才足夠呢？定理四告訴我們：如果 S\subset\mathbb{R}^n，最多只要 n+1 個點便可寫出凸包 \hbox{conv}(S) 中任一點的凸組合表達式。以 \mathbb{R}^2 平面為例，對於任一 \mathbf{x}\in\hbox{conv}(S)，只要找到向量集 S 中三個點使得 \mathbf{x} 位於此三點構成的三角形內即可；或找到兩個點使得 \mathbf{x} 位於這兩點連成的直線段上；甚至，如果 \mathbf{x}\in S，則該點即為自身的凸組合。

 
定理四：若 S\subset\mathbb{R}^n 是一個非空向量集，則任一屬於 \hbox{conv}(S) 的向量必可表示成 S 中 k 個點的凸組合，k\le n+1。

給定 \mathbf{x}\in\hbox{conv}(S)，我們要證明下列表達式存在[1]：\mathbf{x}=c_1\mathbf{v}_1+\cdots+c_k\mathbf{v}_k，其中 \mathbf{v}_i\in S，c_1+\cdots+c_k=1，c_i\ge 0，i=1,\ldots,k，且 k\le n+1。若 k>n+1，則 \{\mathbf{v}_1,\ldots,\mathbf{v}_k\} 必是仿射相依 (見“仿射獨立”，定理三)，也就是說，存在不全為零的數組 d_1,\ldots,d_k 使得

d_1\mathbf{v}_1+\cdots+d_k\mathbf{v}_k=\mathbf{0}

且 d_1+\cdots+d_k=0。考慮

c_1\mathbf{v}_1+\cdots+c_k\mathbf{v}_k=\mathbf{x}。

因為第一式乘以 -1 不造成影響且 d_i 不全為零，故存在 q 使得 c_q/d_q=\min_{d_i>0}\{c_i/d_i\}。置換指標 k 和 q，如此可使 d_k>0 且當 d_i>0 時，c_k/d_k\le c_i/d_i。將第二式減去第一式通乘 c_k/d_k 的結果，消去 \mathbf{v}_k 項，如下：

\displaystyle \left(c_1-\frac{c_k}{d_k}d_1\right)\mathbf{v}_1+\cdots+\left(c_{k-1}-\frac{c_k}{d_k}d_{k-1}\right)\mathbf{v}_{k-1}=\mathbf{x}

令 p_i=c_i-(c_k/d_k)d_i，i=1,\ldots,k-1，且 p_k=0。使用 c_i 和 d_i 的性質，

\displaystyle \sum_{i=1}^kp_i=\sum_{i=1}^nc_i-\frac{d_k}{d_k}\sum_{i=1}^kd_i=1-0=1，

而且每一 p_i\ge 0。理由如下：若 d_i\le 0，則 p_i\ge c_i\ge 0。若 d_i>0，則 p_i=d_i(c_i/d_i-c_k/d_k)\ge 0。所以，

\mathbf{x}=p_1\mathbf{v}_1+\cdots+p_{k-1}\mathbf{v}_{k-1}

是 \mathbf{v}_1,\ldots,\mathbf{v}_{k-1} 的一個凸組合。重複此程序至到 k\le n+1 停止，因為這時仿射相依未必成立。

 
參考來源：
[1] 證明修改自 David C. Lay, Linear Algebra and its Applications, 4th ed., 2012, pp 457-458.

This entry was posted in 線性代數專欄, 仿射幾何 and tagged , , , , . Bookmark the permalink.

5 Responses to 凸組合、凸包與凸集

  1. 張盛東 says:
    05/14/2013 at 11:07 am

    終于能上老師的博客了。最近會大陸，想不到一會去就上不了老師這個網站了。好不容易花錢買了個vpn終于正常上網了。

    Reply
  2. Joshua Leung (@szjoshua) says:
    07/20/2015 at 11:52 pm

    写得非常好，拜读了！
    博客非常不错，是个复习线代的好地方：）

    Reply
  3. missislanderblog says:
    06/23/2017 at 10:03 pm

    老师您好！您这篇文章写得真是太好啦！文笔好可爱～

    Reply

Leave a comment