費雪的判別分析與線性判別分析

本文的閱讀等級：高級

在許多現實應用中，我們往往要面對高維度 (多變數) 數據，為便利分析，降維 (dimension reduction) 常是一個必要的前處理工作。主成分分析 (principal components analysis) 是目前普遍被採用的降維技術 (見“主成分分析”)。主成分分析是一種非教導式學習法 (unsupervised learning)，根據樣本自身的統計性質降維，並不在乎 (甚至不知道) 這些數據的後續應用。在機器學習領域，分類 (classification) 與回歸 (regression) 是兩個最具代表性的問題描述典範。所謂分類是指識別出數據點所屬的類別。本文介紹英國統計學家費雪 (Ronald Fisher) 最早提出的一個專為包含兩個類別樣本所設計的教導式 (supervised) 降維法，稱作費雪的判別分析 (Fisher’s discriminant analysis)，隨後並討論三個延伸問題：

甚麼是線性判別分析 (linear discriminant analysis)？它與費雪的判別分析有何關係？
線性判別分析與最小平方法有甚麼關聯性？
費雪的判別分析如何推廣至多類別 (類別數大於2) 判別分析？

Ronald Fisher (1890-1962) From http://upload.wikimedia.org/wikipedia/commons/4/46/R._A._Fischer.jpg

費雪的判別分析

假設我們有一筆維數等於 $d$ ，樣本大小為 $n$ 的數據 $\{\mathbf{x}_1,\ldots,\mathbf{x}_n\}$ ，也就是說，數據點 $\mathbf{x}_1,\ldots,\mathbf{x}_n$ 散布在 $\mathbb{R}^d$ 空間。假設此樣本包含兩個類別，第一類有 $n_1$ 個數據點，以 $\mathcal{C}_1$ 表示指標集合，第二類有 $n_2$ 個數據點，以 $\mathcal{C}_2$ 表示指標集合， $n_1+n_2=n$ 。費雪提出這個想法：將 $\mathbb{R}^d$ 空間的數據點投影至一穿越原點的直線，以達到降低樣本維數的效果。透過改變直線的指向，我們期望找出一條最佳直線使得兩類數據點於直線的投影盡可能地分離開來，這就是費雪的判別分析的目的。令單位向量 $\mathbf{w}\in\mathbb{R}^d$ ( $\Vert\mathbf{w}\Vert=1$ ) 代表直線 $L$ 的指向，即 $L=\{c\mathbf{w}\vert c\in\mathbb{R}\}$ 。對於任一 $\mathbf{x}\in\mathbb{R}^d$ ，令 $y\mathbf{w}$ 表示 $\mathbf{x}$ 在直線 $L$ 的正交投影。根據正交原則，殘餘量 $\mathbf{x}-y\mathbf{w}$ 正交於 $\mathbf{w}$ (見“正交投影──威力強大的線代工具”)，即有 $\mathbf{w}^T(\mathbf{x}-y\mathbf{w})=0$ ，整理可得

$\displaystyle y=\frac{\mathbf{w}^T\mathbf{x}}{\mathbf{w}^T\mathbf{w}}=\mathbf{w}^T\mathbf{x}$ 。

根據上式，令 $\mathbf{x}_1,\ldots,\mathbf{x}_n$ 至直線 $L$ 的投影量 (投影座標) 為 $y_1,\ldots,y_n$ ，即 $y_i=\mathbf{w}^T\mathbf{x}_i$ ， $1\le i\le n$ 。設定一門檻值 $w_0$ ，立刻得到一個簡單的線性分類法則：若 $\mathbf{w}^T\mathbf{x}\le-w_0$ ，則數據點 $\mathbf{x}$ 歸於第一類 ( $\mathcal{C}_1$ )，否則歸於第二類 ( $\mathcal{C}_2$ )。稍後我們會說明如何決定 $w_0$ ，眼前的問題是：怎麼求出使分類效果最佳的直線指向 $\mathbf{w}$ ？

直覺上，為了獲致最好的分類效果，我們希望分屬兩類別的數據點的投影距離越遠越好。寫出兩個類別數據點的各自樣本中心 (樣本平均數向量)：

$\displaystyle \mathbf{m}_j=\frac{1}{n_j}\sum_{i\in\mathcal{C}_j}\mathbf{x}_i,~~~j=1,2$ 。

投影量的樣本平均數就是樣本中心的投影，如下：

$\displaystyle m_j=\frac{1}{n_j}\sum_{i\in\mathcal{C}_j}y_i=\frac{1}{n_j}\sum_{i\in\mathcal{C}_j}\mathbf{w}^T\mathbf{x}_i=\mathbf{w}^T\mathbf{m}_j,~~~j=1,2$ 。

因此，兩類別的樣本中心投影的距離為

$\displaystyle \vert m_2-m_1\vert=\left|\mathbf{w}^T(\mathbf{m}_2-\mathbf{m}_1)\right|$ 。

由於我們已經加入限制 $\Vert\mathbf{w}\Vert=1$ ，樣本中心投影的距離平方 $(m_2-m_1)^2$ ，稱為組間散布 (between-class scatter)，不會隨著 $\mathbf{w}$ 的長度變化而無限制地增大。使用 Lagrange 乘數法可解出 $\mathbf{w}$ 使最大化組間散布平方 (見“Lagrange 乘數法”)：

$\displaystyle\begin{aligned} L(\lambda,\mathbf{w})&=\left(\mathbf{w}^T(\mathbf{m}_2-\mathbf{m}_1)\right)^2-\lambda(\mathbf{w}^T\mathbf{w}-1)\\ &=\mathbf{w}^T(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T\mathbf{w}-\lambda(\mathbf{w}^T\mathbf{w}-1), \end{aligned}$

其中 $\lambda$ 是 Lagrange 乘數。計算偏導數 (見“矩陣導數”)，

$\displaystyle \frac{\partial L}{\partial\mathbf{w}}=2(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T\mathbf{w}-2\lambda\mathbf{w}$ 。

令上式等於零，因為 $(\mathbf{m}_2-\mathbf{m}_1)^T\mathbf{w}$ 為一純量，立得 $\mathbf{w}\propto\mathbf{m}_2-\mathbf{m}_1$ ，再予以歸一化即可。這個做法有一個明顯的缺點。下圖左顯示二類數據點在平面上有良好的散布區隔，但投影至連接樣本中心的直線後反而產生嚴重的交疊。這個現象發生的原因在於描述數據點的兩個變數存在顯著的共變異，換句話說，兩變數之間的相關係數不為零 (見“相關係數”)。為了克服這個問題，費雪建議直線指向 $\mathbf{w}$ 不僅要使樣本中心的投影分離開來，同時還要使同一組內的投影變異越小越好，如圖右。

二類別數據點投影至不同的直線

定義兩類別的投影樣本的組內散布 (within-class scatter) 為

$\displaystyle s_j^2=\sum_{i\in\mathcal{C}_j}(y_i-m_j)^2,~~j=1,2$ 。

將組內散布 $s_j^2$ 除以 $(n_j-1)$ 即為組內樣本變異數 (見“樣本平均數、變異數和共變異數”)。整體的投影樣本組內散布為 $s_1^2+s_2^2$ 。費雪提出的準則為最大化組間散布和整體組內散布的比值：

$\displaystyle J(\mathbf{w})=\frac{(m_2-m_1)^2}{s_1^2+s_2^2}$ 。

下面解說如何求出使上式最大的單位向量 $\mathbf{w}$ 。定義組內散布矩陣

$\displaystyle S_j=\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{x}_i-\mathbf{m}_j)^T,~~j=1,2$ ，

以及整體組內散布矩陣 $S_W=S_1+S_2$ 。對於 $j=1,2$ ，組內散布 $s_j^2$ 可表示為組內散布矩陣 $S_j$ 的二次型：

$\displaystyle\begin{aligned} s_j^2&=\sum_{i\in\mathcal{C}_j}\left(\mathbf{w}^T\mathbf{x}_i-\mathbf{w}^T\mathbf{m}_j\right)^2\\ &=\sum_{i\in\mathcal{C}_j}\mathbf{w}^T(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{x}_i-\mathbf{m}_j)^T\mathbf{w}\\ &=\mathbf{w}^T\left(\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{x}_i-\mathbf{m}_j)^T\right)\mathbf{w}\\ &=\mathbf{w}^TS_j\mathbf{w}.\end{aligned}$

整體組內散布即為

$\displaystyle s_1^2+s_2^2=\mathbf{w}^TS_1\mathbf{w}+\mathbf{w}^TS_2\mathbf{w}=\mathbf{w}^TS_W\mathbf{w}$ 。

類似地，定義組間散布矩陣

$\displaystyle S_B=(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T$ 。

組間散布 $(m_2-m_1)^2$ 也可表示為組間散布矩陣 $S_B$ 的二次型：

$\displaystyle\begin{aligned} (m_2-m_1)^2&=\left(\mathbf{w}^T\mathbf{m}_2-\mathbf{w}^T\mathbf{m}_1\right)^2\\ &=\mathbf{w}^T(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T\mathbf{w}\\ &=\mathbf{w}^TS_B\mathbf{w}. \end{aligned}$

組內散布矩陣 (在不造成混淆的情況下，整體組內散布矩陣簡稱為組內散布矩陣) $S_W$ 是一個對稱半正定矩陣。如果 $n>d$ ， $S_W$ 通常是正定矩陣，也就是可逆矩陣，以下假設如此。組間散布矩陣 $S_B$ 是樣本中心差 $\mathbf{m}_2-\mathbf{m}_1$ 的外積 (outer product)，因此是對稱半正定；當 $\mathbf{m}_1\neq\mathbf{m}_2$ (絕大多數的應用都滿足此條件)， $\text{rank}S_B=1$ 。

使用組間散布和組內散布的二次型表達，費雪準則可用矩陣式表示為

$\displaystyle J(\mathbf{w})=\frac{\mathbf{w}^TS_B\mathbf{w}}{\mathbf{w}^TS_W\mathbf{w}}$ 。

最大化費雪準則等價於下列約束優化問題 (見“Hermitian 矩陣特徵值的變化界定”)：

$\displaystyle \max_{\mathbf{w}^TS_W\mathbf{w}=1}\mathbf{w}^TS_B\mathbf{w}$

使用 Lagrange 乘數法不難推導出最佳條件式。這裡我們介紹一個線性代數方法：費雪準則也稱為廣義 Rayleigh 商，最大化 $J(\mathbf{w})$ 等價於求解廣義特徵值問題 (見“廣義特徵值問題”)：

$\displaystyle S_B\mathbf{w}=\lambda S_W\mathbf{w}$ 。

由於 $S_W$ 是可逆矩陣，廣義特徵值問題退化為一般特徵值問題 $S_W^{-1}S_B\mathbf{w}=\lambda\mathbf{w}$ 。因為 $S_W^{-1}$ 和 $S_B$ 都是半正定， $S_W^{-1}S_B$ 的特徵值 $\lambda$ 為非負數 (見“Hermitian 矩陣乘積的性質”，定理二)，保證 $\mathbf{w}$ 必然是實特徵向量。廣義特徵方程左乘 $\mathbf{w}^T$ ， $\mathbf{w}^TS_B\mathbf{w}=\lambda\mathbf{w}^TS_W\mathbf{w}$ ，可知費雪準則為 $J(\mathbf{w})=\lambda$ ，因此我們要挑選出最大的特徵值。但 $\text{rank}(S_W^{-1}S_B)=\text{rank}S_B=1$ ，表示 $S_W^{-1}S_B$ 僅有唯一一個正特徵值。寫出特徵方程的顯式表達 $\displaystyle S_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T\mathbf{w}=\lambda\mathbf{w}$ ，忽略式中的純量，對應唯一正特徵值的特徵向量為

$\displaystyle \mathbf{w}\propto S_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$ 。

直白地說，最佳投影直線的指向即為連接兩類別樣本中心的向量於排除組內散布效應後的方向 (如上圖右所示)。

線性判別分析

費雪的判別分析其實是一個應用於兩類別樣本的降維方法，它本身並不具備判別功能。如欲將費雪的判別分析引進分類功能，我們還須決定分類法則 $\mathbf{w}^T\mathbf{x}\le -w_0$ 的門檻值 $w_0$ ，這個分類法稱為線性判別分析 (linear discriminant analysis，簡稱 LDA)。線性判別分析假設分類樣本的條件密度 $p(\mathbf{x}\vert \mathcal{C}_1)$ 和 $p(\mathbf{x}\vert\mathcal{C}_2)$ 服從常態分布 (見“共變異數矩陣與常態分布”)：

$\displaystyle \mathcal{N}(\mathbf{x}\vert\boldsymbol{\mu}_j,\Sigma)=\frac{1}{(2\pi)^{d/2}\vert\Sigma\vert^{1/2}}\exp\left\{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu}_j)^T\Sigma^{-1}(\mathbf{x}-\boldsymbol{\mu}_j)\right\}$ ，

其中 $\boldsymbol{\mu}_j\in\mathbb{R}^d$ 是類別 $\mathcal{C}_j$ 的平均數向量， $\Sigma$ 是 $d\times d$ 階共變異數矩陣 (covariance matrix)， $\vert\Sigma\vert$ 表示 $\Sigma$ 的行列式。請特別注意，線性判別分析假設兩類別有相同的共變異數矩陣 $\Sigma$ ，也就是說，兩類別的數據點具有相同的散布型態。

給定一數據點 $\mathbf{x}\in\mathbb{R}^d$ ，如何判定它應歸類於 $\mathcal{C}_1$ 抑或 $\mathcal{C}_2$ ？貝氏定理 (Bayes’ theorem) 提供了解答 (見“貝氏定理──量化思考的利器”)：

$\displaystyle P(\mathcal{C}_j\vert\mathbf{x})=\frac{p(\mathbf{x}\vert\mathcal{C}_j)P(\mathcal{C}_j)}{p(\mathbf{x})}$ ，

其中

$P(\mathcal{C}_j)$ 是類別 $\mathcal{C}_j$ 出現的機率，稱為先驗機率 (priori probability)；
$p(\mathbf{x}\vert\mathcal{C}_j)$ 是條件密度函數，即給定類別 $\mathcal{C}_j$ ，數據點 $\mathbf{x}$ 的機率密度函數，也稱為似然 (likelihood)；
$p(\mathbf{x})$ 是數據點 $\mathbf{x}$ 的機率密度函數，稱為證據 (evidence)，算式為

$p(\mathbf{x})=p(\mathbf{x}\vert\mathcal{C}_1)P(\mathcal{C}_1)+p(\mathbf{x}\vert\mathcal{C}_2)P(\mathcal{C}_2)$ ；
$P(\mathcal{C}_j\vert\mathbf{x})$ 是指在給定數據點 $\mathbf{x}$ 的情況下，該點屬於 $\mathcal{C}_j$ 的機率，稱為後驗機率 (posterior probability)。

所謂貝氏最佳分類器就是將數據點 $\mathbf{x}$ 的類別指定給最大後驗機率所屬的類別：若 $P(\mathcal{C}_1\vert\mathbf{x})\ge P(\mathcal{C}_2\vert\mathbf{x})$ ，則 $\mathbf{x}$ 歸於第一類，否則歸於第二類。因為對數函數 $\log (\cdot)$ 是一個單調遞增函數， $P(\mathcal{C}_1\vert\mathbf{x})\ge P(\mathcal{C}_2\vert\mathbf{x})$ 等價於 $\log P(\mathcal{C}_1\vert\mathbf{x})\ge \log P(\mathcal{C}_2\vert\mathbf{x})$ 。此外，後驗機率 $P(\mathcal{C}_1\vert\mathbf{x})$ 和 $P(\mathcal{C}_2\vert\mathbf{x})$ 有相同的分母 $p(\mathbf{x})$ ，我們大可直接比較分子的大小。所以，貝氏最優分類法則可以改寫為：若 $\log p(\mathbf{x}\vert\mathcal{C}_1)+\log P(\mathcal{C}_1)\ge \log p(\mathbf{x}\vert\mathcal{C}_2)+\log P(\mathcal{C}_2)$ ，則 $\mathbf{x}$ 歸於第一類，否則歸於第二類。

考慮第一類數據點 $\mathbf{x}$ ，將多變量常態分布代入 $p(\mathbf{x}\vert\mathcal{C}_j)$ ，移除常數部分，得到不等式

$\displaystyle -\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu}_1)^T\Sigma^{-1}(\mathbf{x}-\boldsymbol{\mu}_1)+\log P(\mathcal{C}_1)\ge -\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu}_2)^T\Sigma^{-1}(\mathbf{x}-\boldsymbol{\mu}_2)+\log P(\mathcal{C}_2)$ ，

乘開化簡可得

$\displaystyle (\boldsymbol{\mu}_2-\boldsymbol{\mu}_1)^T\Sigma^{-1}\mathbf{x}\le\frac{1}{2}\boldsymbol{\mu}_2^T\Sigma^{-1}\boldsymbol{\mu}_2-\frac{1}{2}\boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1-\log P(\mathcal{C}_2)+\log P(\mathcal{C}_1)$ 。

因此，線性判別分析的分類法則如下：若 $\mathbf{w}^T\mathbf{x}\le -w_0$ ，則 $\mathbf{x}$ 歸於第一類，否則歸於第二類，其中

$\displaystyle\begin{aligned} \mathbf{w}&=\Sigma^{-1}(\boldsymbol{\mu}_2-\boldsymbol{\mu}_1)\\ w_0&=-\frac{1}{2}\boldsymbol{\mu}_2^T\Sigma^{-1}\boldsymbol{\mu}_2+\frac{1}{2}\boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1+\log P(\mathcal{C}_2)-\log P(\mathcal{C}_1). \end{aligned}$

給定一訓練樣本，先驗機率 $P(\mathcal{C}_j)$ 以類別樣本出現的頻率 $n_j/n$ 估計，類別平均數向量 $\boldsymbol{\mu}_j$ 以樣本平均數向量 $\mathbf{m}_j$ 估計，共變異數矩陣 $\Sigma$ 則以加權平均 (有偏) 共變異數矩陣 $S$ 估計，其中

$\displaystyle\begin{aligned} S&=\left(\frac{n_1}{n}\right)\frac{1}{n_1}\sum_{i\in\mathcal{C}_1}(\mathbf{x}_i-\mathbf{m}_1)(\mathbf{x}_i-\mathbf{m}_1)^T+\left(\frac{n_2}{n}\right)\frac{1}{n_2}\sum_{i\in\mathcal{C}_2}(\mathbf{x}_i-\mathbf{m}_2)(\mathbf{x}_i-\mathbf{m}_2)^T\\ &=\frac{1}{n}(S_1+S_2)=\frac{1}{n}S_W.\end{aligned}$

採用估計量的線性判別分析給出

$\displaystyle \mathbf{w}=nS_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$ ，

這與費雪的判別分析的最佳直線有相同的指向，同時並確定了判別門檻

$\displaystyle w_0=-\frac{n}{2}\mathbf{m}_2^TS_W^{-1}\mathbf{m}_2+\frac{n}{2}\mathbf{m}_1^TS_W^{-1}\mathbf{m}_1+\log \frac{n_2}{n}-\log \frac{n_1}{n}$ 。

最小平方法

線性判別分析給出分隔兩類別的線性邊界 $\mathbf{w}^T\mathbf{x}=-w_0$ ，我們不免好奇這個邊界可否從最小平方法推導？的確可行，構想是將兩類別的分類問題改寫成回歸問題。考慮線性回歸模型 $g(\mathbf{x})=\mathbf{w}^T\mathbf{x}+w_0$ 。若樣本數據點 $\mathbf{x}_i$ 屬於第一類，則設目標值為 $n/n_1$ ；若 $\mathbf{x}_i$ 屬於第二類，設目標值為 $-n/n_2$ 。定義最小平方誤差函數

$\displaystyle E=\frac{1}{2}\sum_{i=1}^n\left(g(\mathbf{x}_i)-r_i\right)^2=\frac{1}{2}\sum_{i=1}^n\left(\mathbf{w}^T\mathbf{x}_i+w_0-r_i\right)^2$ ，

其中 $r_i=n/n_i$ 若 $i\in\mathcal{C}_1$ ， $r_i=-n/n_2$ 若 $i\in\mathcal{C}_2$ 。計算偏導數，

$\displaystyle\begin{aligned} \frac{\partial E}{\partial w_0}&=2\sum_{i=1}^n(\mathbf{w}^T\mathbf{x}_i+w_0-r_i)\\ \frac{\partial E}{\partial \mathbf{w}}&=2\sum_{i=1}^n(\mathbf{w}^T\mathbf{x}_i+w_0-r_i)\mathbf{x}_i. \end{aligned}$

令上面兩式為零。由 $\frac{\partial E}{\partial w_0}=0$ 可解出

$\displaystyle\begin{aligned} w_0&=-\frac{1}{n}\sum_{i=1}^n\mathbf{w}^T\mathbf{x}_i+\sum_{i=1}^nr_i\\ &=-\mathbf{w}^T\left(\frac{1}{n}\sum_{i=1}^n\mathbf{x}_i\right)+n_1\frac{n}{n_1}-n_2\frac{n}{n_2}\\ &=-\mathbf{w}^T\mathbf{m}. \end{aligned}$

將解得的 $w_0$ 表達式代入 $\frac{\partial E}{\partial\mathbf{w}}=\mathbf{0}$ ，整理化簡可得 (推導過程見^[1])

$\displaystyle \left(S_W+\frac{n_1n_2}{n}S_B\right)\mathbf{w}=n(\mathbf{m}_1-\mathbf{m}_2)$ ，

展開即有

$\displaystyle\begin{aligned} S_W\mathbf{w}&=-\frac{n_1n_2}{n}(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T\mathbf{w}+n(\mathbf{m}_1-\mathbf{m}_2)\\ &=\left(-\frac{n_1n_2}{n}(\mathbf{m}_2-\mathbf{m}_1)^T\mathbf{w}-n\right)(\mathbf{m}_2-\mathbf{m}_1). \end{aligned}$

不計純量，則得

$\displaystyle \mathbf{w}\propto S_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$ 。

因為 $\mathbf{w}$ 的長度不影響邊界 $\mathbf{w}^T\mathbf{x}-\mathbf{w}^T\mathbf{m}=0$ ，直接設 $\mathbf{w}=S_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)$ ，可得分類法則：若 $\mathbf{w}^T\mathbf{x}\le\mathbf{w}^T\mathbf{m}$ ，則 $\mathbf{x}$ 歸為第一類，否則歸為第二類。原因如下：代入 $\mathbf{x}=\mathbf{m}_1$ ，則

$\displaystyle\begin{aligned} \mathbf{w}^T(\mathbf{m}_1-\mathbf{m})&=(\mathbf{m}_2-\mathbf{m}_1)^TS_W^{-1}\left(\mathbf{m}_1-\frac{n_1}{n}\mathbf{m}_1-\frac{n_2}{n}\mathbf{m}_2\right)\\ &=-\frac{n_2}{n}(\mathbf{m}_2-\mathbf{m}_1)S_W^{-1}(\mathbf{m}_2-\mathbf{m}_1)<0, \end{aligned}$

上面不等式係因 $S_W^{-1}$ 是正定矩陣。費雪的判別分析、線性判別分析和最小平方法導出同樣的直線指向 $\mathbf{w}$ 。請讀者自行驗證：當 $n_1=n_2=n/2$ ，最小平方法和線性判別分析給出相同的分類邊界 $\mathbf{w}^T\mathbf{x}+w_0=0$ 。

多類別判別分析

費雪的判別分析限定於包含兩類別的樣本，後續學者將它推廣至 $k>2$ 類別的情況，即 $\mathcal{C}_1,\ldots,\mathcal{C}_k$ 。首先，我們推廣組內散布矩陣和組間散布矩陣。多類別的組內散布矩陣可由 $k=2$ 延伸而得，

$\displaystyle S_W=\sum_{j=1}^kS_j$ ，

其中

$\displaystyle S_j=\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{x}_i-\mathbf{m}_j)^T,~~~j=1,\ldots,k,$

且

$\displaystyle \mathbf{m}_j=\frac{1}{n_j}\sum_{i\in\mathcal{C}_j}\mathbf{x}_i,~~~j=1,\ldots,k$ ，

上式中 $n_1+\cdots+n_k=n$ 。不過，組間散布矩陣的適切推廣則不明顯。我們從另一個方向著手。定義整體樣本平均數向量 $\mathbf{m}$ 和整體散布矩陣 $S_T$ 為

$\displaystyle \mathbf{m}=\frac{1}{n}\sum_{i=1}^n\mathbf{x}_i=\frac{1}{n}\sum_{j=1}^k\sum_{i\in\mathcal{C}_j}\mathbf{x}_i=\frac{1}{n}\sum_{j=1}^kn_j\mathbf{m}_j$

$\displaystyle S_T=\sum_{i=1}^n(\mathbf{x}_i-\mathbf{m})(\mathbf{x}_i-\mathbf{m})^T$ 。

使用上面兩式化簡整體散布矩陣 $S_T$ ，過程如下：

$\displaystyle\begin{aligned} S_T&=\sum_{j=1}^k\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j+\mathbf{m}_j-\mathbf{m})(\mathbf{x}_i-\mathbf{m}_j+\mathbf{m}_j-\mathbf{m})^T\\ &=\sum_{j=1}^k\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{x}_i-\mathbf{m}_j)^T+\sum_{j=1}^k\sum_{i\in\mathcal{C}_j}(\mathbf{m}_j-\mathbf{m})(\mathbf{m}_j-\mathbf{m})^T\\ &~~+\sum_{j=1}^k\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{m}_j-\mathbf{m})^T+\sum_{j=1}^k(\mathbf{m}_j-\mathbf{m})\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j)^T\\ &=S_W+\sum_{j=1}^k n_j(\mathbf{m}_j-\mathbf{m})(\mathbf{m}_j-\mathbf{m})^T. \end{aligned}$

這個結果提示了組間散布矩陣可定義為 (此定義於先前二類別定義的差異見註解^[2])

$\displaystyle S_B=\sum_{j=1}^k n_j(\mathbf{m}_j-\mathbf{m})(\mathbf{m}_j-\mathbf{m})^T$ ，

即有， $S_T=S_W+S_B$ 。

我們引進 $q\ge 1$ 個單位向量 $\mathbf{w}_1,\ldots,\mathbf{w}_q$ ，對應 $q$ 個直線。對於任一 $\mathbf{x}\in\mathbb{R}^d$ ，分別投影至 $\mathbf{w}_1,\ldots,\mathbf{w}_q$ 所指的直線可得 $q$ 個線性特徵：

$\displaystyle y_l=\mathbf{w}_l^T\mathbf{x},~~l=1,\ldots,q$ ，

或合併為矩陣形式

$\displaystyle \mathbf{y}=\begin{bmatrix} y_1\\ \vdots\\ y_q \end{bmatrix}=\begin{bmatrix} \mathbf{w}_1^T\mathbf{x}\\ \vdots\\ \mathbf{w}_q^T\mathbf{x} \end{bmatrix}=\begin{bmatrix} \mathbf{w}_1&\cdots&\mathbf{w}_q \end{bmatrix}^T\mathbf{x}=W^T\mathbf{x}$ ，

其中 $W=\begin{bmatrix} \mathbf{w}_1&\cdots&\mathbf{w}_q \end{bmatrix}$ 是 $d\times q$ 階矩陣。令 $\mathbf{y}_1,\ldots,\mathbf{y}_n\in\mathbb{R}^q$ 表示樣本 $\mathbf{x}_1,\ldots,\mathbf{x}_n\in\mathbb{R}^d$ 於 $\mathbf{w}_l$ ， $1\le l\le q$ ，的投影，即 $\mathbf{y}_i=W^T\mathbf{x}_i$ ， $i=1,\ldots,n$ 。如同 $\{\mathbf{x}_i\}$ 有 $d\times d$ 階組內散布矩陣和組間散布矩陣， $\{\mathbf{y}_i\}$ 也可定義 $q\times q$ 階組內散布矩陣和組間散布矩陣：

$\displaystyle\begin{aligned} \tilde{S}_W&=\sum_{j=1}^k \sum_{i\in\mathcal{C}_j}(\mathbf{y}_i-\tilde{\mathbf{m}}_j)(\mathbf{y}_i-\tilde{\mathbf{m}}_j)^T\\ \tilde{S}_B&=\sum_{j=1}^k n_j(\tilde{\mathbf{m}}_j-\tilde{\mathbf{m}})(\tilde{\mathbf{m}}_j-\tilde{\mathbf{m}})^T, \end{aligned}$

其中

$\displaystyle \tilde{\mathbf{m}}_j=\frac{1}{n_j}\sum_{i\in\mathcal{C}_j}\mathbf{y}_i=\frac{1}{n_j}\sum_{i\in\mathcal{C}_j}W^T\mathbf{x}_i=W^T\mathbf{m}_j,~~j=1,\ldots,k$

$\displaystyle \tilde{\mathbf{m}}=\frac{1}{n}\sum_{j=1}^k n_j\tilde{\mathbf{m}}_j=\frac{1}{n}\sum_{j=1}^k n_j W^T\mathbf{m}_j=W^T\mathbf{m}.$

定義於 $\{\mathbf{x}_i\}$ 的組內及組間散布矩陣和定義於 $\{\mathbf{y}_i\}$ 的組內及組間散布矩陣的關係如下：

$\displaystyle\begin{aligned} \tilde{S}_W&=\sum_{j=1}^k \sum_{i\in\mathcal{C}_j}W^T(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{x}_i-\mathbf{m}_j)^TW=W^TS_WW\\ \tilde{S}_B&=\sum_{j=1}^k n_jW^T(\mathbf{m}_j-\mathbf{m})(\mathbf{m}_j-\mathbf{m})^TW=W^TS_BW. \end{aligned}$

接下來將定義於兩類別的費雪準則推廣至 $k>2$ 個類別。常見的目標函數有兩種，一為跡數表達式^[3]，另一為行列式表達式^[4]，分述於下：

$\displaystyle J_1(W)=\text{trace}\left(\tilde{S}_W^{-1}\tilde{S}_B\right)=\text{trace}\left((W^TS_WW)^{-1}(W^TS_BW)\right)$

和

$\displaystyle J_2(W)=\frac{\det \tilde{S}_B}{\det \tilde{S}_W}=\frac{\det(W^TS_BW)}{\det(W^TS_WW)}$ 。

有趣的是，這兩個準則有相同的最佳條件：

$\displaystyle S_B\mathbf{w}_l=\lambda_lS_W\mathbf{w}_l,~~l=1,\ldots,q$ ，

其中 $\mathbf{w}_l$ 是廣義特徵向量，對應廣義特徵值 $\lambda_l$ 。由於推導涉及跡數和行列式的導數，過程不免繁瑣，欲深入了解的讀者請見註解^[5]和^[6]。提醒讀者， $\mathbf{w}_1,\ldots,\mathbf{w}_q$ 亦為 $S_W^{-1}S_B$ 的特徵向量，對應非負特徵值 $\lambda_1,\ldots,\lambda_q$ 。另外， $S_W^{-1}$ 是正定矩陣，推知 $S_W^{-1}S_B$ 可對角化 (見“Hermitian 矩陣乘積的性質”，定理四)，也就是說， $\{\mathbf{w}_1,\ldots,\mathbf{w}_q\}$ 為一線性獨立集。但 $S_W^{-1}S_B$ 並非對稱矩陣 (除非 $S_W^{-1}$ 和 $S_B$ 是可交換矩陣)，故 $\{\mathbf{w}_1,\ldots,\mathbf{w}_q\}$ 並不是一個單範正交集 (orthonormal set)。最後說明 $q$ 的大小限制。我們可以證明 $\tilde{S}_W^{-1}\tilde{S}_B$ 和 $S_W^{-1}S_B$ 有相同的特徵值 $\lambda_1,\ldots,\lambda_q$ (見註解^[5])。為了方便，下面用 $J_1(W)$ 來解說。目標函數 $J_1(W)$ 可表示為

$\displaystyle J_1(W)=\lambda_1+\cdots+\lambda_q$ 。

因為加入零特徵值不會加大 $J_1(W)$ ，我們要求 $\lambda_1,\ldots,\lambda_q$ 都是正特徵值，故 $q=\text{rank}(\tilde{S}_W^{-1}\tilde{S}_B)$ 。另一方面， $\tilde{\mathbf{m}}$ 是 $\tilde{\mathbf{m}}_1,\ldots,\tilde{\mathbf{m}}_k$ 的線性組合，

$\displaystyle \text{rank}(\tilde{S}_W^{-1}\tilde{S}_B)=\text{rank}\tilde{S}_B=\dim\text{span}\{\tilde{\mathbf{m}}_1-\tilde{\mathbf{m}},\ldots,\tilde{\mathbf{m}}_k-\tilde{\mathbf{m}}\}\le k-1$ ，

故 $q\le k-1$ 。給定包含 $k\ge 2$ 個類別的樣本，多類別判別分析所能產生的有效線性特徵總數至多為 $k-1$ 。

在確保樣本保有最佳分類效果的前提下，多類別判別分析將 $d$ 維數據點 $\mathbf{x}_1,\ldots,\mathbf{x}_n$ 壓縮至 $q\le k-1$ 維數據點 $\mathbf{y}_1,\ldots,\mathbf{y}_n$ 。針對降維後的新樣本，如何設計有效的多類別分類器呢？這是機器學習領域的熱門研究主題，日後我將陸續為讀者介紹一些應用普及的方法與技術。

註解
[1] 先證明下列等式：

$\displaystyle S_W=\sum_{i=1}^n\mathbf{x}_i\mathbf{x}_i^T-n_1\mathbf{m}_1\mathbf{m}_1^T-n_2\mathbf{m}_2\mathbf{m}_2^T$ 。

直接乘開組內散布矩陣 $S_j$ ， $j=1,2$ ，可得

$\displaystyle\begin{aligned} S_j&=\sum_{i\in\mathcal{C}_j}(\mathbf{x}_i-\mathbf{m}_j)(\mathbf{x}_i-\mathbf{m}_j)^T\\ &=\sum_{i\in\mathcal{C}_j}\mathbf{x}_i\mathbf{x}_i^T-\mathbf{m}_j\sum_{i\in\mathcal{C}_j}\mathbf{x}_i^T-\sum_{i\in\mathcal{C}_j}\mathbf{x}_i\mathbf{m}_j^T+n_j\mathbf{m}_j\mathbf{m}_j^T\\ &=\sum_{i\in\mathcal{C}_j}\mathbf{x}_i\mathbf{x}_i^T-\mathbf{m}_j(n_j\mathbf{m}_j^T)-(n_j\mathbf{m}_j)\mathbf{m}_j^T+n_j\mathbf{m}_j\mathbf{m}_j^T\\ &=\sum_{i\in\mathcal{C}_j}\mathbf{x}_i\mathbf{x}_i^T-n_j\mathbf{m}_j\mathbf{m}_j^T, \end{aligned}$

故 $S_W=S_1+S_2=\sum_{i=1}^n\mathbf{x}_i\mathbf{x}_i^T-n_1\mathbf{m}_1\mathbf{m}_1^T-n_2\mathbf{m}_2\mathbf{m}_2^T$ 。寫出

$\displaystyle \frac{\partial E}{\partial \mathbf{w}}=2\sum_{i=1}^n(\mathbf{w}^T\mathbf{x}_i+w_0-r_i)\mathbf{x}_i=0$ ，

代入 $w_0=-\mathbf{w}^T\mathbf{m}$ ，得到

$\displaystyle \sum_{i=1}^n\mathbf{x}_i(\mathbf{x}_i^T-\mathbf{m}^T)\mathbf{w}=\sum_{i=1}^nr_i\mathbf{x}_i$ 。

等號左邊化簡如下：

$\displaystyle\begin{aligned} \sum_{i=1}^n\mathbf{x}_i(\mathbf{x}_i^T-\mathbf{m}^T)\mathbf{w}&=\left(\sum_{i=1}^n\mathbf{x}_i\mathbf{x}_i^T-n\mathbf{m}\mathbf{m}^T\right)\mathbf{w}\\ &=\left(\sum_{i=1}^n\mathbf{x}_i\mathbf{x}_i^T-\frac{1}{n}(n_1\mathbf{m}_1+n_2\mathbf{m}_2)(n_1\mathbf{m}_1+n_2\mathbf{m}_2)^T\right)\mathbf{w}\\ &=\left(\sum_{i=1}^n\mathbf{x}_i\mathbf{x}_i^T-n_1\mathbf{m}_1\mathbf{m}_1^T-n_2\mathbf{m}_2\mathbf{m}_2^T+\frac{n_1n_2}{n}(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T\right)\mathbf{w}\\ &=\left(S_W+\frac{n_1n_2}{n}S_B\right)\mathbf{w}. \end{aligned}$

等號右邊為

$\displaystyle \sum_{i=1}^nr_i\mathbf{x}_i=\frac{n}{n_1}\sum_{i\in\mathcal{C}_1}\mathbf{x}_i-\frac{n}{n_2}\sum_{i\in\mathcal{C}_2}\mathbf{x}_i=n(\mathbf{m}_1-\mathbf{m}_2)$ 。

[2] 對於兩類別情況 (即 $k=2$ )，多類別組間散布矩陣為

$\displaystyle S_B=n_1(\mathbf{m}_1-\mathbf{m})(\mathbf{m}_1-\mathbf{m})^T+n_2(\mathbf{m}_2-\mathbf{m})(\mathbf{m}_2-\mathbf{m})^T$ ，

其中

$\displaystyle\begin{aligned} \mathbf{m}_1-\mathbf{m}&=\mathbf{m}_1-\frac{1}{n}(n_1\mathbf{m}_1+n_2\mathbf{m}_2)=\frac{n_2}{n}(\mathbf{m}_1-\mathbf{m}_2)\\ \mathbf{m}_2-\mathbf{m}&=\mathbf{m}_2-\frac{1}{n}(n_1\mathbf{m}_1+n_2\mathbf{m}_2)=\frac{n_1}{n}(\mathbf{m}_2-\mathbf{m}_1). \end{aligned}$

因此， $S_B$ 可化簡為

$\displaystyle S_B=\frac{n_1n_2}{n}(\mathbf{m}_2-\mathbf{m}_1)(\mathbf{m}_2-\mathbf{m}_1)^T$ ，

上式與費雪的判別分析使用的二類別的組間散布矩陣的差異僅在於 $n_1n_2/n$ ，乘入常數於費雪準則 $J(\mathbf{w})$ 不會對最佳解造成任何影響。

[3] Christopher M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006, pp 192.

[4] Richard O. Duda, Peter E. Hart, and David G. Stork, Pattern Classification, 2nd ed., John Wiley & Sons, 2001, pp 123.

[5] 對於目標函數

$\displaystyle J_1(W)=\text{trace}\left((W^TS_WW)^{-1}(W^TS_BW)\right)$ ，

使用跡數的導數恆等式 (見“跡數與行列式的導數”，tr-20)，

$\displaystyle\begin{aligned} \frac{\partial J_1}{\partial W}&=\frac{\partial\text{trace}\left((W^TS_WW)^{-1}(W^TS_BW)\right)}{\partial W}\\ &=-2S_WW(W^TS_WW)^{-1}W^TS_BW(W^TS_WW)^{-1}+2S_BW(W^TS_WW)^{-1}. \end{aligned}$

令 $\frac{\partial J_1}{\partial W}=0$ ，並右乘 $W^TS_WW$ ，可得最佳條件式

$\displaystyle S_BW=S_WW(W^TS_WW)^{-1}W^TS_BW$ ，

或表示為

$\displaystyle S_BW=S_WW\tilde{S}^{-1}_W\tilde{S}_B$ 。

我們需要這個性質： $\tilde{S}_W$ 是對稱正定矩陣且 $\tilde{S}_B$ 是對稱矩陣，則存在一 $q\times q$ 階可逆矩陣 $P$ 使得 $P^T\tilde{S}_WP$ 和 $P^T\tilde{S}_BP$ 為對角矩陣 (見“廣義特徵值問題”)。證明於下 (詳見“每週問題 July 15, 2013”)：因為 $\tilde{S}_W$ 是對稱正定矩陣，可知存在一可逆矩陣 $M$ 使得 $\tilde{S}_W=M^TM$ (見“正定矩陣的性質與判別方法”)。不難確認 $(M^{-1})^T\tilde{S}_BM^{-1}$ 是對稱半正定，故存在一正交矩陣 $Q$ ， $Q^T=Q^{-1}$ ，使得 $(M^{-1})^T\tilde{S}_BM^{-1}=QDQ^T$ ，其中 $D=\text{diag}(\lambda_1,\ldots,\lambda_q)$ 且 $\lambda_l\ge 0$ ， $1\le l\le q$ 。設 $P=M^{-1}Q$ ，則

$\displaystyle P^T\tilde{S}_WP=Q^T(M^{-1})^TM^TMM^{-1}Q=Q^TQ=I$

且

$\displaystyle P^T\tilde{S}_BP=Q^T(M^{-1})^T\tilde{S}_BM^{-1}Q=Q^TQDQ^TQ=D$ 。

將上面二式改寫為 $\tilde{S}^{-1}_W=PP^T$ 和 $\tilde{S}_B=(P^T)^{-1}DP^{-1}$ ，合併可得

$\displaystyle \tilde{S}_W^{-1}\tilde{S}_B=PDP^{-1}$ ，

也就是說 $\lambda_1,\ldots,\lambda_q$ 是 $\tilde{S}_W^{-1}\tilde{S}_B$ 的特徵值。將上式代入最佳條件式，可得

$\displaystyle S_BWP=S_WWPD$ 。

令 $d\times q$ 階矩陣 $U=WP$ 。以 $U$ 取代 $W$ 來計算目標函數，使用跡數循環不變性，可得

$\displaystyle\begin{aligned} J_1(U)&=\text{trace}\left((U^TS_WU)^{-1}(U^TS_BU)\right)\\ &=\text{trace}\left((P^TW^TS_WWP)^{-1}(P^TW^TS_BWP)\right)\\ &=\text{trace}\left(P^{-1}(W^TS_WW)^{-1}(P^T)^{-1}P^T(W^TS_BW)P\right)\\ &=\text{trace}\left((W^TS_WW)^{-1}(W^TS_BW)PP^{-1}\right)\\ &=\text{trace}\left((W^TS_WW)^{-1}(W^TS_BW)\right)\\ &=J_1(W). \end{aligned}$

對於任何可逆矩陣 $P$ ， $J_1(WP)=J_1(W)$ 總是成立，換句話說，目標函數 $J_1$ 完全由 $W$ 的行空間 (column space) 所決定。既然 $U=WP$ 和 $W$ 有相同的目標函數值，我們可以用 $U$ 替換 $W$ ，最佳條件式即為

$\displaystyle S_BU=S_WUD$ 。

以行向量表示 $U=\begin{bmatrix} \mathbf{u}_1&\cdots&\mathbf{u}_q \end{bmatrix}$ ，則有廣義特徵方程

$\displaystyle S_B\mathbf{u}_l=\lambda_lS_W\mathbf{u}_l,~~l=1,\ldots,q$ 。

我們推得一個重要的結論： $d\times d$ 階 $S_W^{-1}S_B$ 和 $q\times q$ 階 $\tilde{S}_W^{-1}\tilde{S}_B$ 有相同的 $q$ 個非負特徵值 $\lambda_1,\ldots,\lambda_q$ 。

[6] 對於目標函數

$\displaystyle J_2(W)=\frac{\det(W^TS_BW)}{\det(W^TS_WW)}$ ，

取對數可得

$\displaystyle \log J_2(W)=\log\det(W^TS_BW)-\log\det(W^TS_WW)$ 。

這麼做的原因是對數函數不會改變極值的位置。使用行列式的導數恆等式 (見“跡數與行列式的導數”，det-10)，

$\displaystyle \frac{\partial \log J_2}{\partial W}=2S_BW(W^TS_BW)^{-1}-2S_WW(W^TS_WW)^{-1}$ 。

令 $\frac{\partial \log J_2}{\partial W}=0$ ，並右乘 $W^TS_BW$ ，可得

$\displaystyle S_BW=S_WW(W^TS_WW)^{-1}W^TS_BW$ ，

此即註解^[5]所導出的最佳條件式。以 $U=WP$ ( $P$ 為一可逆矩陣) 替換 $W$ ，目標函數為

$\displaystyle\begin{aligned} J_2(U)&=\frac{\det(U^TS_BU)}{\det(U^TS_WU)}\\ &=\frac{\det(P^TW^TS_BWP)}{\det(P^TW^TS_WWP)}\\ &=\frac{(\det P^T)\det(W^TS_BW)(\det P)}{(\det P^T)\det(W^TS_WW)(\det P)}\\ &=\frac{\det(W^TS_BW)}{\det(W^TS_WW)}\\ &=J_2(W).\end{aligned}$

這說明 $J_2$ 完全由 $W$ 的行空間所決定，複製^[5]的論證過程，最佳條件式為

$\displaystyle S_BU=S_WUD$ 。

11 Responses to 費雪的判別分析與線性判別分析

ccjou says:

03/14/2014 at 4:37 pm

本文過長，我校讀過二遍，如果讀者發現仍有錯誤請不吝指正，謝謝。

張盛東 says:

03/15/2014 at 2:47 pm

周老師，我有個疑問：
文中，“直白地說，最佳投影直線的指向即為連接二個類別樣本中心的向量於排除組內散布效應後的方向 (如上圖左所示)。”

這裡是否應該是“如上圖右所示”？

- ccjou says:
  
  03/15/2014 at 10:52 pm
  
  謝謝，你眼力真好！我後來也發現了這個錯誤，已訂正。還有沒有別的錯誤？特別是註解，記號實在非常繁雜。
  
  - 張盛東 says:
    
    03/17/2014 at 3:00 pm
    
    老師，我剛才把註解部分看了一遍，覺得應該沒有任何問題。
    
    謝謝老師的文章，令我對LDA背後的理論有更深刻的理解。
    
student says:

10/28/2014 at 7:04 pm

周老師您好
您提到在兩類別資料中求取w時
如果 n>d，Sw 通常是正定矩陣
此時的特例應該是n>d時資料矩陣還是可能是 singular matrix
而原本應是求解廣義特徵值問題也因為 Sw與Sb 的inverse不存在而無法轉換
因此想請問您有甚麼辦法能在不刪除線性相依變數的前提下進行LDA呢?

- ccjou says:
  
  10/28/2014 at 9:32 pm
  
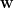  如果 $S_W$ 是不可逆矩陣，你可以在主對角元加入一個很小的擾動量 $\epsilon>0$ ，成為 $S_W+\epsilon I$ 。不過，解出的 $\mathbf{w}$ 將隨 $\epsilon$ 的大小改變。
  
duby says:

07/04/2017 at 7:19 am

周老師，我有兩個的疑問：1多分類情況的目標函數的含義。以不相互正交基底的共變異數矩陣的行列式的意義？2多分類下，最大特征值對應的特征向量分割性能最好，最小特征值對應的特征向量分割性能最差，為什麼還要選它呢？

- ccjou says:
  
  07/13/2017 at 2:23 pm
  
  1) 矩陣的行列式等於所有特徵值之積；
  2) 這些特徵向量都是兩兩正交，即便特徵值小的特徵向量仍具備分割能力。
  
frank says:

06/09/2018 at 5:44 pm

謝謝周老師的介紹，實在非常詳盡，含括大部分推導細節，很棒的文章，受益良多。
發現一個很小的錯誤，但不影響其他式子的推導：在線性判別分析，一開始提到的多變量常態分布函數，$(2\pi)$的指數應是$\frac{d}{2}$喔。

Pingback: 費雪的判別分析與線性判別分析 | 不分享空間
ZhengNaijun says:

04/10/2019 at 3:44 pm

你好，我觉公式3 可以写成arg max trace(A)/trace(B), 这样求导更简单，而不必是arg max trace(inv(A)B)

	陳倍恩 on 線性代數的第一堂課──矩陣乘法的定義
	輕鬆談如何教學二項式定理？… on 牛頓的二項式定理 (上)
	madhouse on 高斯消去法
	WishMobile on 翻轉 LU 分解
	周子傑 on Karush-Kuhn-Tucker (KKT) 條件
	Cloud Huang on 線性泛函與伴隨