本文的閱讀等級:中級
我們曾經在“可對角化矩陣的譜分解──續篇(上)”證明譜定理 (spectrum theorem) 的反向命題:若 階矩陣
可表示為
,
其中 為相異數,
是非零矩陣並滿足
,
,以及
,則
可對角化 (若未註明階數,以下
表示
階單位矩陣
)。本文介紹一個採用建構式的證明,我們的思路是從給定條件先推論
是冪等 (idempotent) 矩陣,從而導出
的對角化形式
,其中
,每一
,表明
是
的特徵值,
是特徵向量矩陣。這個證明所使用的線性代數定理與分析方法包括分塊矩陣的保秩變換、秩─零度定理、可對角化矩陣的成立條件、秩分解 (rank decomposition),以及透過相似變換用跡數來計算秩。為便於閱讀,我將證明分成幾個步驟。(本文的證明由網友Meiyue Shao提供,原始文本請見“Spectral_decomposition”。)
(1) 是冪等矩陣,即
。
使用 ,
,和
,可得
。
(2) ,
。
運用向量空間分析即可證明,請讀者參閱“特殊矩陣 (5):冪等矩陣”。下面介紹採用形如相合變換 (congruence transformation) 的分塊矩陣運算證法,
是可逆矩陣 (見“相合變換”)。寫出
以及
。
上面的變換矩陣皆可逆,故不改變矩陣秩,也就有
(3) 冪等矩陣 可對角化,且特徵值屬於
,
。
令 為
的特徵值。因為
,可知
,故
或
,對應的特徵空間分別是
和
,這裡
表示矩陣的零空間 (nullspace)。使用秩─零度定理 (見“使用輸入輸出模型活化秩─零度定理”),
。
令兩式相加,使用 (2) 可得 ,其中
和
分別是特徵值
與
的幾何重數 (最大線性獨立的特徵向量數)。特徵值的幾何重數不大於代數重數 (特徵值的相重數) (見“幾何重數不大於代數重數的證明”),而所有相異特徵值的代數重數和等於矩陣的階數
,推論特徵值
和
的代數重數等於幾何重數,所以
是可對角化矩陣 (見“可對角化矩陣與缺陷矩陣的判定”)。
(4) 存在 階矩陣
和
使得
,其中
(命題給定
為非零矩陣),
。
設 可對角化為
,
其中 稱為秩分解 (見“秩分解──目視行秩等於列秩”),
由特徵向量矩陣
的前
個行 (column) 組成,
由
的前
個列 (row) 組成。
(5) ,即
。
矩陣的跡數等於特徵值之和,由 (4) 可知 。所以,
(6) 和
是
階矩陣,且
。
由 (4) 和 (5) 確定 和
是
階方陣,且
(7) 是可對角化矩陣。
由 (6),。使用 (4),
的對角化形式推導如下:
上式稱為譜分解 (spectral decomposition),表明 有相異的特徵值
(互異性已由命題給定),
階分塊
的行空間 (
的行空間) 即為對應
的特徵空間
。
最後再補充一個快捷的證法。令 階矩陣
的相異特徵值為
,對應特徵值
的代數重數為
,指標 (index,最大 Jordan 分塊階數) 為
。矩陣
可對角化等價於以下任一條件 (見“最小多項式 (下)”):
- 對於每一特徵值
,幾何重數都等於代數重數,即
。
- 對於每一特徵值
,對應指標皆為
。
- 矩陣
的 Jordan 形式的所有 (基本) Jordan 分塊階數皆為
。
- 最小多項式 (minimal polynomial) 為
。
我們可以利用最小多項式來證明 (3) 和 (2)。寫出 ,立知
是
的一個消滅多項式 (或稱零化多項式)。因為不可能存在次數更小的消滅多項式,
是
的最小多項式,由上述可對角化條件4:最小多項式不含重根推得 (3)
可對角化。因此,特徵值
的幾何重數
與特徵值
的幾何重數
滿足
。使用兩次秩─零度定理,可得 (2) 的矩陣秩公式:
既然最小多項式可證明冪等矩陣 可對角化,何不直接應用於證明譜定理?為方便說明,下面考慮
的情況:
,
其中 ,
,且
。我們的目標是證明
,
即表明 的最小多項式為
。計算過程如下:
最後一個等式乃因所有展開項都包含 ,
。對於一般情況,
,不難確認
同樣成立。
從冪等矩陣出發到最終推得對角化形式的論證過程包含七個步驟,看似大費周章。最小多項式證法一蹴可幾,既省時又省力,何樂而不為?速度與效率並非檢驗事物良窳的唯一標準,我們往往還要考量行為背後的動機與目的。就學習而論,我的想法是乘坐直升機登玉山還不如一步一腳印慢走塔塔加鞍部步道欣賞沿途的綺麗風光來得有趣。

非常感谢您的分享,我是在中国大陆百度做数据挖掘的工程师,请问您能共享您的pdf文件或课件吗
歡迎轉載,但請留意兩岸的一些用詞差異:
您好,请教一个肤浅的问题:算子和矩阵一样吗?共轭算子和共轭矩阵呢?谢谢 Regan
请教老师一个肤浅的问题,算子和矩阵有什么不一样?二者可等同吗?共轭算子和共轭矩阵呢?谢谢
令 為一向量空間。線性變換
為一向量空間。線性變換 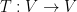 稱為線性算子。如果
稱為線性算子。如果 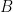 是
是  的一基底,則
的一基底,則 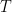 參考基底
參考基底 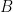 的表示矩陣
的表示矩陣 ![A=[T]_B](https://s0.wp.com/latex.php?latex=A%3D%5BT%5D_B&bg=ffffff&fg=000000&s=0&c=20201002) 為一
為一  階方陣,
階方陣,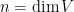 。反過來說,任一
。反過來說,任一  階方陣
階方陣  是一個定義於幾何向量空間
是一個定義於幾何向量空間 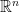 (或
(或 ) 的線性算子,即
) 的線性算子,即 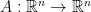 。相關討論見
。相關討論見