忽必烈大汗注意到馬可波羅的城市,彼此之間很類似,似乎從一個城市到另一個城市的移轉,不是旅程,而是元素的變換。現在,忽必烈大汗的心靈從馬可波羅描述的城市自行出發,在一點一點地拆解了這座城市之後,他以另一種方式重新構築,換掉組成部分,移動或翻轉它們。───卡爾維諾 (Italo Calvino) 《看不見的城市》
與線性方程解有關的分解
LU 分解
適用對象: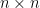 階矩陣
階矩陣 
分解形式: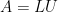 ,
,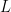 是下三角方陣,
是下三角方陣, 是上三角方陣。注意,LU 分解未必總是存在。
是上三角方陣。注意,LU 分解未必總是存在。
QR 分解
適用對象: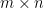 階矩陣
階矩陣 
分解形式: ,
,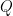 是
是  階正交 (orthogonal) 矩陣,
階正交 (orthogonal) 矩陣,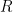 是
是 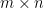 階上三角矩陣。
階上三角矩陣。
- Gram-Schmidt 正交化與 QR 分解
- 線代膠囊──QR 分解
- Householder 變換於 QR 分解的應用
- Givens 旋轉於 QR 分解的應用
- Gram-Schmidt 正交化改良版
- QR 分解的數值計算方法比較
Cholesky 分解
適用對象: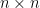 階實對稱正定矩陣
階實對稱正定矩陣 
分解形式: ,
, 是下三角矩陣且主對角元皆為正數。
是下三角矩陣且主對角元皆為正數。
奇異值分解 (Singular value decomposition)
適用對象: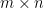 階矩陣
階矩陣 
分解形式: ,
, 是
是  階正交矩陣,
階正交矩陣,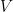 是
是 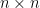 階正交矩陣,
階正交矩陣, 是
是 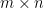 階對角矩陣且主對角元皆不為負數。若
階對角矩陣且主對角元皆不為負數。若  是複矩陣,則
是複矩陣,則  ,
, 和
和 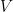 是么正 (unitary) 矩陣。
是么正 (unitary) 矩陣。
與特徵值有關的分解
譜分解 (Spectral decomposition),或稱特徵分解或對角化
適用對象: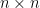 階矩陣
階矩陣 
分解形式: ,
, 是由
是由  的特徵值構成的對角矩陣,
的特徵值構成的對角矩陣, 的行向量為對應的特徵向量。注意,譜分解未必總是存在。
的行向量為對應的特徵向量。注意,譜分解未必總是存在。
正交譜分解,或稱正交對角化
適用對象: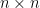 階實對稱矩陣 (或 Hermitian 矩陣)
階實對稱矩陣 (或 Hermitian 矩陣) 
分解形式: (或
(或  ),
), 是由
是由  的特徵值構成的對角矩陣,
的特徵值構成的對角矩陣,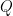 (或
(或  ) 是正交矩陣 (或 么正矩陣) 其行向量為對應的特徵向量。
) 是正交矩陣 (或 么正矩陣) 其行向量為對應的特徵向量。
Schur 分解
適用對象: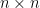 階矩陣
階矩陣 
分解形式: ,
,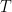 是上三角矩陣,
是上三角矩陣, 是么交矩陣。
是么交矩陣。
Jordan 分解
適用對象: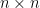 階矩陣
階矩陣 
分解形式: ,
,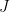 是
是  的 Jordan 形式,
的 Jordan 形式, 的行向量為對應的廣義特徵向量。
的行向量為對應的廣義特徵向量。
其他分解
極分解 (Polar decomposition)
適用對象: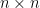 階矩陣
階矩陣 
分解形式: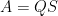 ,
,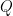 是正交矩陣,
是正交矩陣, 是半正定矩陣。若
是半正定矩陣。若  是複矩陣,則
是複矩陣,則 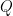 是么正矩陣。
是么正矩陣。
二對稱矩陣分解
適用對象: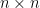 階矩陣
階矩陣 
分解形式: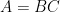 ,
,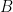 是可逆對稱矩陣,
是可逆對稱矩陣,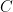 是對稱矩陣。
是對稱矩陣。
秩分解
適用對象: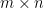 階矩陣
階矩陣 
分解形式: ,
,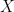 是
是 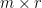 階矩陣,
階矩陣, 是
是  階矩陣,
階矩陣,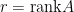 。
。
等價標準型
適用對象: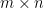 階矩陣
階矩陣 
分解形式: ,
,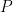 是
是  階可逆矩陣,
階可逆矩陣,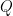 是
是 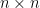 階可逆矩陣,
階可逆矩陣,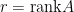 。
。

版主好,
不只矩陣有分解,我從網路上找到三階張量分解:
Click to access kolda_2008.pdf
Click to access FCP_TSP_final_doublecol.pdf
三階張量也具有rank,是矩陣的高維類比