本文的閱讀等級:中級
實對稱矩陣是線性代數中用途最廣泛的特殊矩陣,主要原因在於實對稱矩陣可用來表達二次型 (見“二次型與正定矩陣”,“Hermitian 矩陣與實對稱矩陣的一些實例”)。實對稱矩陣具備一些特殊的數學性質:所有的特徵值都是實數,並有完整的單範正交 (orthonormal,兩兩正交且長度等於 1) 特徵向量,也就是說,實對稱矩陣是可正交對角化的 (orthogonally diagonalizable)。令 為一個
階實對稱矩陣且
為
的特徵值。所謂正交對角化是指存在一個實正交矩陣 (orthogonal matrix)
,
,使得
,其中
的行向量 (column vector) 即為
的單範正交特徵向量,
是由特徵值構成的對角矩陣。實對稱矩陣是正規矩陣 (normal matrix) 家族的一員,滿足
,其中
(見“特殊矩陣 (2):正規矩陣”)。正規矩陣的一個標記性質是可么正對角化 (unitarily diagonalizable),即
,其中
是一個么正矩陣 (unitary matrix),滿足
,因此立刻推論實對稱矩陣是可正交對角化的。
本文介紹另一個不常見於教科書的實對稱矩陣可正交對角化的證明方法,此法結合了一些重要的線性代數分析技巧,包括不變子空間 (invariant subspace)、正交補餘 (orthogonal complement),以及分塊矩陣運算,值得讀者詳加探究。本文內容可以直接推廣至 Hermitian 矩陣,你只要將實數系 替換為複數系
,並將轉置
替換為共軛轉置
即可 (見“特殊矩陣 (9):Hermitian 矩陣”)。
考慮一個 階實對稱矩陣
。因為
,對於
中任意向量
和
,就有
。
稍後你會發現這是整個分析過程中最重要的關鍵式。
定理一:實對稱矩陣的特徵值皆是實數,且對應特徵向量是實向量。
設 ,
,
且
。等號兩邊同取共軛,就有
,再取轉置,
。
因為 是實對稱矩陣,
,上式等同於
。
此式右乘 並代入特徵方程式,等號左邊為
,
等號右邊為 ,合併即得
。
但是 (除非
),故可推論
。換句話說,特徵值
必為實數,推論特徵空間
(
的零空間) 為
的子空間,故
是一個非零實向量。
底下介紹一個更快捷的推導 (見“答chang──關於線性代數的學習改進方法”)。使用前述關鍵式 ,等號左邊與右邊分別可化簡為
令上面兩式相等即得證。
定理二:實對稱矩陣對應相異特徵值的特徵向量互為正交。
根據定理一,以下實對稱矩陣 的特徵值皆為實數,對應的特徵向量皆為實向量。設
,
,且
。第二式左乘
,就有
。
第一式取轉置,,再右乘
,即得
。
因為 ,上面兩式等號左邊相同,所以
。
已知 ,推得
,即
。這裡補充另一個作法,使用關鍵式
,等號左邊與右邊分別可化簡為
。
定理三:令 為實對稱矩陣
的特徵向量。若
,則
。
設 且
。套用關鍵式,可得
,
推知 正交於
。
由定理二和定理三尚不足以證明 階實對稱矩陣
擁有完整的
個兩兩互為正交的特徵向量,你需要其他輔助工具。我們視
為定義於
的線性算子,即
。考慮子空間
,令
代表
經
映射所得的像
。若
,即
必有
,則
稱為
的一個不變子空間。注意,對應特徵值
的特徵空間
也是
的一個不變子空間,因為若
,則
(詳細討論請見“不變子空間──解構線性算子的利器”)。
定理四:令 為一個實對稱矩陣。若
是
的一個不變子空間,則正交補餘
也是
的一個不變子空間。
因為 是
的一個不變子空間,對於任一
,
。若
,則
,也就有
。
這指出 ,證明
也是
的一個不變子空間。
定理五:任一 階實對稱矩陣都有
個單範正交特徵向量。
證明1:定理一說明實對稱矩陣 必有一個實特徵向量
(設
) 對應實特徵值
,即
。令
,顯然,
,
。令
為
的一組單範正交基底。對於
,以下關係成立:
,
,且
,若
。我們知道
是
的不變子空間,定理四說明
也是
的不變子空間,因此所有
都屬於
,故有
。
將 ,
合併為矩陣形式,如下:
。
以 代表等號右邊的
階分塊,並令
,
是正交矩陣。上式可表示為
,
左乘 ,即得
,
取轉置又得到
。
使用 ,可知
,
也是實對稱矩陣。再繼續對
階矩陣
執行上述步驟,可得
階正交矩陣
使得
,
其中 為
階實對稱矩陣。令
,不難驗證
是一個
階正交矩陣,也就有
重複此程序可歸納得
。
令 ,正交矩陣的乘積亦為正交矩陣:
於是導出
。
將正交矩陣 以行向量表示,
,則上式可表示為
,
此即 ,
,對應特徵值
的特徵向量就是正交矩陣
的行向量
。
證明2:使用反證法。假設實對稱矩陣 至多有
個單範正交特徵向量
,分別對應特徵值
。令
。對於任一
,存在唯一組合式
,則
,可知
是
的一個不變子空間,定理四表明
也是
的一個不變子空間。在不變子空間
,必定存在單位特徵向量
使得
(見“拒絕行列式的特徵分析”,定理一),因此
是一個單範正交特徵向量集。這與前提矛盾,推知
,即
有
個單範正交特徵向量。
定理五表明實對稱矩陣 有單範正交特徵向量
,因此可當作
的基底。矩陣
參考有序基底
的表示矩陣即為
,證得實對稱矩陣可正交對角化,即有下列譜分解 (spectral decomposition) 或稱譜定理:
上面令 ,
。重要的是
是正交投影矩陣,滿足下列性質 (見“可對角化矩陣的譜分解”):
,
;
,若
;
。
美國數學教授哈爾莫斯 (Paul R. Halmos) 在他的大作《有限維向量空間》(Finite-Dimensional Vector Spaces) 中說[1]:「現在我們準備好要證明本書最主要的定理,本章其他結果大多是這個定理的立即推論。」哈爾莫斯提到的最主要的定理就是實對稱矩陣的譜定理 (廣義地說,Hermitian 變換的譜定理)。
註解
[1] 頁155,原文:“We are now ready to prove the main theorem of this book, the theorem of which most of the other results of this chapter are immediate corollaries.”

老师,我是香港中文大学的学生,你对线代的理解真是深入,我很敬佩你,我要把这里的所有的资料反复严读,好好做题。期待我对线代有个新的体悟
歡迎來訪。羅馬不是一天造成的,我估計學好線代要花一年的時間。所以不必急,如果累了,可以看看「無關線代」,放鬆一下。
請問老師:
文中提到,使用 A^T=A,可知B_1^T=B_1 , B_1也是實對稱矩陣。
這是為什麼呢?
其中
是哪一部分推理使你疑惑呢?
喔喔,我看懂了,感謝老師
老師您好:看了您的文章真的讓我獲益良多,真的非常感謝您!
這裡有一個問題想請教老師,如果有兩個同屬R^N的正規正交基底(V1…Vn) (W1…Wn)
那是否會有一個獨特的正交運算子T使得T(Vi)=Wi呢?如果有要如何證明? 謝謝您!
可能是你對其中某個概念不清楚,我覺得你自己應該可以解決這個問題。我將問題切成三個子問題: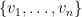 和
和 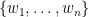 是
是 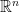 的兩組基底,是否存在唯一的線性變換
的兩組基底,是否存在唯一的線性變換 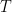 使得
使得 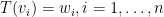 ?是的,證明請見
?是的,證明請見
(1) 若
(2) 那麼如何得到
(3) 你說
正交矩陣。所以
補充說明:若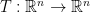 為一正交算子,則對於任一
為一正交算子,則對於任一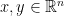 必有
必有 ,反之亦然。設
,反之亦然。設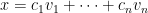 ,
, ,則
,則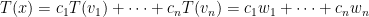 ,同理
,同理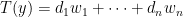 。利用正規正交性質,不難證明
。利用正規正交性質,不難證明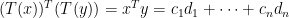 。
。
謝謝老師~看來我的觀念還是沒有很清楚,我會繼續努力的^_^*
老師好,
我想問說可以用Schur定理說A與某個上三角矩陣相似,
再用A^T=A的條件證明此上三角矩陣實為對角矩陣,
然後說A可以被對角化嗎?
可以的,你提出的證明步驟與下文的證法雷同:
因為Schur定理給出正交相似關係,故對稱矩陣可正交對角化。
謝謝老師
看了您的证明,我明白了这个定理被你构造出来。但是,我想知道,直白的说这个定理是怎么被发现的呢?也就是说人们原处是怎么想到这个命题的呢?
每次有人問起數學發現總會讓我冒出一身冷汗。不知道為甚麼,數學家絕少提及他們發現某個定理的歷程,後人只好發揮想像力編纂故事。
我的指導教授曾說:「做研究本來就是沒事找事幹。」數學發現也常是午後打發時間等著吃晚飯前的無聊活動的結果。我們知道實正交矩陣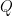 滿足
滿足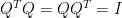 。若
。若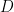 是主對角矩陣,那麼
是主對角矩陣,那麼 是甚麼矩陣?又有甚麼性質?不難得到
是甚麼矩陣?又有甚麼性質?不難得到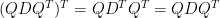 ,
, 是對稱矩陣!於是有了這個猜想:反過來說,任一對稱矩陣
是對稱矩陣!於是有了這個猜想:反過來說,任一對稱矩陣 都可分解成
都可分解成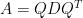 嗎?
嗎?
定理一只證明了實對稱矩陣如果有特徵值,則此特徵值為實數.似乎沒有證明存在性.而定理五引用了定理一使用到了特徵值得存在性,但在這篇文章裡面似乎沒有被提及.
因為特徵值定義為特徵多項式的根,多數的文章都默認任一方陣存在一特徵值。如果不採用此定義,特徵值的存在性證明請見下文定理一:
因為現在矩陣時實係數,所以特徵多項式不一定有實根.這裡周老師使用的是把實數域塞在複數域裡頭.所以假設了複數域的存在.但要做此擴張的話,必須要把所討論的向量空間換成是複數域上的進而在取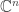 的『實部』與『虛部』然後證明所有的計算都可以workout.當然原因最主要的是:『本文中使用的
的『實部』與『虛部』然後證明所有的計算都可以workout.當然原因最主要的是:『本文中使用的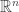 為實向量空間,而非複向量空間.』
為實向量空間,而非複向量空間.』
但為了解決此問題,有兩種做法.用微積分可以理解的做法是.考慮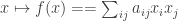 這個函數在
這個函數在 的限制條件下的極值.利用拉格朗日方法,可以證明極值會是
的限制條件下的極值.利用拉格朗日方法,可以證明極值會是 的特徵值,取到的向量
的特徵值,取到的向量 會是特徵向量.這樣就不需要使用到特徵多項式的根,這個特質.因為特徵值的定義本來就不是使用特徵多項式,而是使用
會是特徵向量.這樣就不需要使用到特徵多項式的根,這個特質.因為特徵值的定義本來就不是使用特徵多項式,而是使用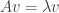 這個線性方程.(剛好當
這個線性方程.(剛好當 是有限微的方陣時,可以使用行列式來說明.)
是有限微的方陣時,可以使用行列式來說明.)
我個人的感想是,討論實對稱方陣的特徵值問題,證明特徵值的存在避免不了分析學(微積分)的使用.但如果使用了域的擴張(把 塞到
塞到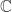 )中,那麼證明應該會更加繁瑣一點.
)中,那麼證明應該會更加繁瑣一點.
上文的證明(定理一)並未定義特徵多項式也不引用行列式,而是使用更本質的「代數基本定理」:任一
雖然從二次型極值的存在性可以證明特徵值存在,但線性代數通常視之為特徵分析的應用,見下文:
另一個實對稱矩陣有實特徵值的更簡單證法是直接證明 Hermitian 矩陣有實特徵值,
這是為什麼多數線性代數的特徵分析都喜歡建立在複數域而非實數域。
代數基本定理是需要在複數域上的.有限維向量空間上的線性算子必存在特徵值這個必須要在『複向量空間』才會成立.在實向量空間中,因為實數域不是代數封閉,所以我們無法做多項式的因式分解.邏輯上來說,除非已經先證明特徵值存在.不然此篇文章的證明使用到了複數域的性質的話就必須要修改.
引用:邏輯上來說,除非已經先證明特徵值存在.不然此篇文章的證明使用到了複數域的性質的話就必須要修改.
論說敘事總會設定某個基礎或前提,不然的話只要每次寫出:「設 為
為 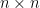 階實矩陣的特徵值,滿足
階實矩陣的特徵值,滿足  ,非零向量
,非零向量 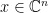 」,我們都要先證明這樣的
」,我們都要先證明這樣的  確實存在。
確實存在。
當然你可以認為因為沒有先證明上面的假設成立,所以邏輯上不嚴謹。
我的意思是在實數向量空間上的存在.因為這裡引用到了這件事情.我想周老師似乎不太理解我想表達的.在第一個定理的證明中,使用到了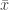 .在複數向量空間中我們才會用
.在複數向量空間中我們才會用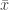 .其實第一個定理證明其實就是我說的,把
.其實第一個定理證明其實就是我說的,把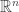 中嵌入到
中嵌入到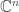 中去看把
中去看把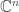 (as a 集合)=
(as a 集合)= .然後使用的是複數的內積,也是周老師裡面寫的
.然後使用的是複數的內積,也是周老師裡面寫的 .因為任何的實矩陣可以看成是複數矩陣.所以其特徵多項式有根.接著證明特徵值必定是實數.然後證明
.因為任何的實矩陣可以看成是複數矩陣.所以其特徵多項式有根.接著證明特徵值必定是實數.然後證明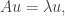 其中
其中 是在
是在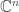 中的實數部分.也就是說
中的實數部分.也就是說 且方程
且方程 是在
是在 中成立.此時我們把
中成立.此時我們把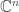 的real part 跟
的real part 跟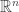 視為等同.所以這個是周老師證明中所使用到的地方.否則,在實數的世界中是看不到複數的.而這個證明中,我們是把
視為等同.所以這個是周老師證明中所使用到的地方.否則,在實數的世界中是看不到複數的.而這個證明中,我們是把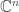 的實部看成是我們要使用的
的實部看成是我們要使用的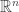 .把實對稱矩陣看成是複數矩陣.因為周老師的證明中沒有很清楚地提到這些“向量”是活在哪個域上的“向量空間”.在不同的域(非代數封閉的域)上解方程,想法上會有些不同.所以提出了我的看法跟說明.
.把實對稱矩陣看成是複數矩陣.因為周老師的證明中沒有很清楚地提到這些“向量”是活在哪個域上的“向量空間”.在不同的域(非代數封閉的域)上解方程,想法上會有些不同.所以提出了我的看法跟說明.
我還是不清楚你的論點,所以在網路上找了一些相關討論,請參考:
http://farside.ph.utexas.edu/teaching/336k/Newtonhtml/node66.html
Click to access 46%20Symmetric%20Matrices.pdf
(下文Lemma 0.1)
Click to access 340_symmetric.pdf
老師您好,
我關於”定理五”的推導還是有一些疑惑
推導中好像只使用到”A是對稱矩陣”的條件
但沒有使用到 “A是””實數””對稱矩陣” 的條件
所以是不是只要是對稱矩陣,就算是複數對稱矩陣,也可以正交對角化呢?
謝謝老師!
定理五的證明1與2都使用了定理四:若 為實對稱矩陣
為實對稱矩陣  的一不變子空間,則正交補集
的一不變子空間,則正交補集  亦為
亦為  的一個不變子空間。
的一個不變子空間。
定理四不適用於複對稱矩陣 (從證明可以看出來)。事實上,複對稱矩陣不可正交對角化,譬如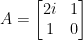 有特徵值
有特徵值 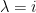 ,代數重數是2,但僅有一個特徵向量
,代數重數是2,但僅有一個特徵向量 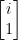 。
。
不過,複對稱矩陣可「對角化」為 (但不是正交對角化)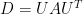 ,其中
,其中 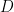 是對角矩陣,
是對角矩陣, 是unitary矩陣,
是unitary矩陣, (但
(但 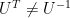 )。這個分解式稱為Autonne–Takagi factorization,見
)。這個分解式稱為Autonne–Takagi factorization,見
https://en.wikipedia.org/wiki/Symmetric_matrix#Complex_symmetric_matrices
喔喔,原來如此,謝謝老師!
新年快樂!
老師您好:
所以實對稱矩陣做Schur分解後的上三角矩陣ㄧ定為對角矩陣嗎?
感謝老師!
是的。設 Schur 分解為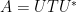 ,
,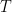 是上三角矩陣,
是上三角矩陣, ,則
,則 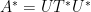 。因此,
。因此,
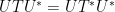 ,左乘
,左乘 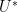 ,右乘
,右乘  ,得到
,得到 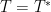 ,推論
,推論  是實對角矩陣。
是實對角矩陣。
瞭解! 謝謝老師明瞭的回覆~
請問: 特徵值必為實數我看得懂但是 為什麼特徵空間一定是R^n的子空間。
換句話說就是,若有個複向量滿足Ax=λx 那x一定是某個實向量的複數倍 對吧?
這樣說也可以,但x與A都佈於實數不是很好嗎?
我想通了 一時卡住 不好意思
老師您好: 想請問一下,一矩陣若可正交對角化,是否代表該矩陣也可逆呢?
零矩陣也可正交對角化
我想问一下,有哪篇文章提到了证明对称矩阵相关性质的文章。我看了Introduction to Linear 4ed中的证明,其中证明eigenvalues和pivots有相同的符号,但是这句话我无法理解:Since these eigenvalues cannot cross zero as they move into the pivots, their signs cannot change.
谢谢老师了
这个是证明的完整叙述The number of positive eigenvalues of A = A^T equals the number of positive pivots. We repeat the proof for any A = LDL^T. Move L toward I, by moving the off-diagonal entries to zero. The pivots are not changing and not zero. The eigenvalues A of LDL^T change to the eigenvalues d of I DI^T. Since these eigenvalues cannot cross zero as they move into the pivots, their signs cannot change.
非常谢谢你的分享,对我有巨大的启发。