本文的閱讀等級:中級
愛爾蘭數學家哈密頓 (William Rowan Hamilton) 將複數 ,其中
是實數,
是虛數單位,延伸為四元數 (quaternion),即一個實數加上三個虛部,
,
其中 是實數,虛數單位
滿足基本公式
。
任一複數 與單位複數
的乘積
可以解讀為點
在二維複數平面逆時針旋轉
徑度 (見“複數的矩陣表示”)。類似地,四元數亦可表示三維空間旋轉,不過這個性質不像複數蘊含平面旋轉那般明顯,因為實在難以想像處於
的四元數如何對
向量執行運算。
我們先回顧四元數的表達與基本運算 (見“四元數”)。為了便利解決幾何問題,不妨將四元數 視為純量─向量和
,其中
,因此三維向量
可以看成實部 (純量) 為零的四元數。對於
和
,四元數加法分別計算純量與向量加法:
。
使用四元數的虛數單位的基本公式可推導出乘法運算規則 (見附註[1]):
,
其中 是點積 (dot product),
是向量積 (外積,cross product)。另一方面,利用分配律,
。
比較上面兩式,我們可以定義「向量乘法」
。
表面上,這個運算非常奇怪,因為 既非向量也不是純量。所謂的「向量乘法」其實是四元數乘法,
,所以「向量乘法」僅有形式上的意義,並不具備幾何意義。以純量─向量和表示的四元數
的共軛、絕對值以及逆元分別為
透過四元數乘法,我們可以設計出定義於 的線性變換。給定一個四元數
,定義
,如下:
,
其中 當作實部等於零的四元數
。套用四元數乘法運算規則,以及外積恆等式
和
(見“答張盛東──關於外積與行列式的關係”),其中
,可得
故證明 。下面列舉
的三個重要性質。
是一個線性變換,也就是說,對於任意
和純量
,
。
使用上述
的展開式,
且
- 若
為單位四元數,即
,則每一
滿足
。
直接計算即可驗證,如下:
,
上面使用了
。這個現象稱為等距同構 (isometry),詳見“等距同構與么正矩陣”。
- 若
為單位四元數,則
,
。
證明於下:
羅德里格旋轉公式
若 為單位四元數,即
,設
且
。因此,存在
使得
且
。令
。每一個單位四元數
定可表示為
,
其中 。我們可以證明:以單位向量
為轉軸,線性變換
代表
逆時針旋轉
徑度。將給定向量
分解成
,其中
是
在轉軸
的正交投影,
代表垂直於
的成分。因為
,我們要證明
不改變
且
將
逆時針旋轉
角度,見下圖。
因為存在唯一 使
,由前述性質 (2) 可知
。利用
,即
,可得
上面令 。注意
垂直於
且
。
最後,將 和
代入
的表達式,使用倍角公式,
證明 即是垂直於轉軸
的平面上
逆時針旋轉
而得的向量。
將單位四元數 代入旋轉變換
的展開式,套用倍角公式和半角公式,推得
上式稱為羅德里格旋轉公式 (Rodrigues’ rotation formula),因法國數學家羅德里格 (Olinde Rodrigues) 而得名。給定 和
,外積運算
可用矩陣乘法表示如下:
,
上面我們定義「外積矩陣」為 。再將內積改寫成
,羅德里格旋轉公式可表示成矩陣形式:
令 表示旋轉軸為
,轉角等於
的
階旋轉矩陣。從上面的羅德里格旋轉公式,可得
其中 ,
,
。轉角
的大小由右手法則決定,即大拇指朝向轉軸的正方向
,其餘四根手指的彎曲方向為旋轉方向。
給定一個單位四元數 ,其中
,利用
公式亦可得到以
表示的旋轉矩陣
,如下:
反之,給定旋轉矩陣 ,如何求出對應的單位四元數
?因為
且
,推得
。不難驗證
註解
[1] 使用分配律與四元數乘法運算規則,
代入
可得



為何ijk = -1 而不是-i之類的
i與j本身不同維度 所以 ij不等於-1
你可以自已試一下:i,j,k是純虛數,如果ijk=-i,會有甚麼結果?
ij = k
ijk = kk =-1
周老師: 的時候,為什麼會用半角
的時候,為什麼會用半角 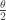 ? 只是單純為了後面的簡化嗎?有沒有更具體和通俗的解釋?
? 只是單純為了後面的簡化嗎?有沒有更具體和通俗的解釋?
您好!
看過您這篇四元數與三維空間旋轉文章後深受啟發,在此先表示感謝。
但我還有一個疑問,就是在選擇單位四元數
WordPress 輸入 LaTeX 的語法須在第一個 $ 後面加入 latex,方可正確顯示。
若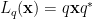 代表三維空間
代表三維空間  以單位向量
以單位向量  為軸旋轉
為軸旋轉  度,則單位四元數
度,則單位四元數 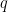 是多少?
是多少?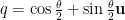 。
。
答案是
若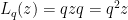 代表複數平面
代表複數平面  旋轉
旋轉  度,則單位複數
度,則單位複數 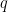 是多少?
是多少? 。
。
答案是
線性變換 $L_q(\mathbf{x})=q\mathbf{x}q^\ast 代表 $\mathbf{x} 逆時針旋轉 $\theta 徑度
那麼座標軸轉換也是一樣的公式嗎?
抱歉不太會用 Latex …
要怎麼做兩個quaternion的轉換呢? 如:已知兩個座標, C0 與 C1,如何用 quaternion 表達兩者的關係?
謝謝老師
我不確定你的問題,兩個座標C0與C1的關係是指下文的哪個問題?
不好意思沒有表達清楚!我想應該是 Q2
我重新詮釋一次問題,再請老師幫我確認是不是Q2:
將空間中的一個座標系 C0 旋轉後得另一座標系 C1,若有一向量 x 在 C0 的座標為 v0 = (x0,y0,z0),在 C1 的座標為 v1 = (x1,y1,z1),請問如何以 quaternion 表示 v0 與 v1 的關係?
會有這個問題是因為在學 robotic kinematics 的時候,學到若C0 經旋轉而得 C1,且C1對應C0 的旋轉矩陣為 R(0:1) ,則上述的 v0 = R(0:1)*v1。若連續旋轉R(0:1), R(1:2),…, R(n-1:n),v0 = R(0:1)*R(1:2)*…*R(n-1:n)*v1。其中R(i-1:i) 為 Ci-1 旋轉成 Ci 的旋轉矩陣。
因為這個,所以想知道是否 quaternion 也有這樣的性質,如:v0 = q*v1 之類的?
不知道這樣有沒有比較清楚~
更正:v0 = R(0:1)*R(1:2)*…*R(n-1:n)*vn
請參閱上文最後一段: ,但計算方式不同,前者是矩陣向量乘法,後者如下:
,但計算方式不同,前者是矩陣向量乘法,後者如下:
其中
阿
老師好奇的請教一下
1878年,英國數學家克利福德才出版Elements of Dynamic
那羅德里格怎麼會使用內積跟外積呢?
https://en.wikipedia.org/wiki/Olinde_Rodrigues
是他先發現這樣的算法之後才有外積內積的定義。