本文的閱讀等級:中級
在二維平面上,逆時針方向旋轉 徑度 (弧度,radian) 的旋轉矩陣為 (見“幾何變換矩陣的設計”)
。
不難驗證 的特徵值為
和
,其中
,並具有下面兩個基本性質:
- 旋轉矩陣
的兩個行向量 (column vector)
和
組成一個單範正交集 (orthonormal set),也就是說,
是一個實正交矩陣 (orthogonal matrix),滿足
,故逆旋轉矩陣為
。
- 對於任一實正交矩陣
,
,即得
。若
,則
稱為適當的 (proper) 正交矩陣。計算
,旋轉矩陣
是適當的正交矩陣。若
,則
稱為不適當的正交矩陣,例如鏡射矩陣 (見“旋轉與鏡射”)
。
本文討論常見於電腦圖學 (computer graphics) 和機器人學的三維空間旋轉,並介紹數種 階旋轉矩陣表示法,包括羅德里格旋轉公式 (Rodrigues’ rotation formula)、Cayley 變換以及歐拉角公式。除此之外,四元數 (quaternion) 亦可表示三維空間旋轉 (見“四元數與三維空間旋轉”)。
歐拉旋轉定理
歐拉 (Leonhard Euler) 於1775年根據簡單的幾何論述證明了這個旋轉定理:在三維空間中,若一個剛體發生位移且剛體內至少有一點固定不動,則此位移等價於一個繞著穿越該固定點的固定軸的旋轉。簡單講,歐拉旋轉定理說:每一個三維空間旋轉皆可表示為對於一個固定軸的旋轉。用線性代數術語來說,若 是一個定義於
的旋轉矩陣,則存在一個非零向量
使得
,我們稱
是對於
的一個不動點 (fixed point),幾何意義是
表示旋轉軸的指向向量,旋轉軸上的每一點
(
是任一實數) 不受旋轉運動而改變。
下面介紹一個歐拉旋轉定理的矩陣證法。令 為一個
階旋轉矩陣,
,且對於任意
,
。
上式稱為等距同構 (isometry),意思是旋轉不改變任兩點之間的距離。正交矩陣等價於等距同構 (見“等距同構與么正矩陣”),換句話說,如同 階旋轉矩陣,每一個
階旋轉矩陣皆為適當的正交矩陣。利用
,
和
,可推得
即有 。所以,旋轉矩陣
有一個特徵值
,對應特徵向量
,即
。
羅德里格旋轉公式
適當的正交矩陣的行列式為 ,實正交矩陣的特徵值的絕對值等於
(見“特殊矩陣 (3):么正矩陣 (酉矩陣)”),且實矩陣若存在複特徵值必然為共軛對 (見“解讀複特徵值”)。因此,由歐拉旋轉定理可推論
階旋轉矩陣
的特徵值為
。旋轉矩陣
滿足
,此為正規 (normal) 矩陣家族的標記 (見“特殊矩陣 (2):正規矩陣”),等價條件是
可么正對角化為
,其中
是么正 (unitary) 矩陣,
,且
。令
,其中
組成一個單範正交集。么正對角化蘊含下列性質:
推得
且
。
推得
(見“矩陣乘法的現代觀點”)。
- 乘開
,
表明
是一個單位實向量,
和
表明
和
是單位複向量。
使用這些性質以及歐拉公式 ,
其中 。因為
和
是實矩陣,上式表明
也是一個實矩陣,則
,
推知 是反對稱矩陣 (見“特殊矩陣 (13):反對稱矩陣”)。令
,其中
。對於任一
,
,可得
,
或改寫為
。
解開上式,
,
其中 是一個待確定的實數。定義「外積矩陣」
,
此名稱由來係因 ,其中
表示向量外積 (cross product,或稱向量積),即有
。使用單範正交集
的基本性質,
再將 代入上式,立得
。我們選擇
,原因是配合慣例使
代表逆時針轉角 (稍後說明)。令
代表一個旋轉矩陣,其特徵值為
且
為對應特徵值
的單位特徵向量。綜合以上結果,旋轉矩陣
的公式如下:
其中 ,
,
。上式稱為羅德里格旋轉公式,
由參數
決定,但實際僅含三個自由參數 (或稱自由度),因為
。另一種解釋是
階適當的正交矩陣
包含
個元,扣除
個限制式
和
,僅存
個自由參數。
羅德里格旋轉公式還可以用「外積矩陣」 表達。使用外積恆等式,
因為 是任一向量,
。所以,
在羅德里格旋轉公式中,單位向量 代表旋轉軸的指向,
是由右手法則所決定的轉角 (即大拇指朝向轉軸正向,其餘四根手指的彎曲方向為旋轉方向)。圖一顯示給定向量
可分解為轉軸成分
(即
至單位向量
的正交投影) 和旋轉成分
,旋轉
後的結果分別如下:
說明轉軸成分不因旋轉而改變,另
說明旋轉成分 在垂直於
的平面上逆時針旋轉
徑度。
考慮反向問題:給定一個 階旋轉矩陣
,求旋轉軸向量
和轉角
。若
,
則 ,故
。
對照羅德里格旋轉公式,不難驗證
。
若限定 ,則轉軸轉角對
和
產生相同的旋轉矩陣,即
。
Cayley 變換
在矩陣理論中,任何一個不含特徵值 的正交矩陣
都可表示為一個反對稱矩陣
的 Cayley 變換 (見“Cayley 變換”),如下:
。
三維空間的旋轉矩陣 是一個
階適當的正交矩陣,將反對稱矩陣
代入 Cayley 變換,計算化簡可得
。
以 Cayley 變換表達的旋轉矩陣的優點是不涉及三角函數,但它有一個限制,即排除了對應特徵值 的旋轉角度
。定義 Cayley 變換而生的旋轉矩陣的三個參數
與轉軸
及轉角
有甚麼關係?下面我們探討這個問題。
寫出羅德里格旋轉矩陣
。
令 。代入三角恆等式
,
旋轉矩陣變成
。
利用冪級數
,
以及 和
,可得
上面使用了 Neumann 無窮級數 (見“Neumann 無窮級數”)。比較 Cayley 變換
和上面的
,可得
,即
,
故得關係式
。
當 ,
未定義,這時 Cayley 變換無法表示旋轉矩陣。
歐拉角公式
羅德里格旋轉矩陣完全由轉軸和轉角決定,因此具備清晰的幾何意義,但由於包含冗餘的參數故不適合描述剛體旋轉運動。歐拉角公式提供了包含三個自由參數的旋轉矩陣設計法。具體地說,任何一個三維空間旋轉皆可表示為三個基本旋轉的複合變換。所謂基本旋轉是指以座標軸X,Y,Z作為旋轉軸。採用右手法則,設 為轉角,稱為歐拉角,
,
,
分別代表對 X,Y 和 Z 軸的旋轉矩陣,如下:
令 表示標準座標系統的基底,並令
、
和
依序表示旋轉過程產生的新基底。任何一個三維空間旋轉可分解成三部分 (見圖二):
- 以
為轉軸,轉角為
,將
和
移動至
和
,且
。
- 以
為轉軸,轉角為
,將
和
移動至
和
,且
。
- 以
為轉軸,轉角為
,將
和
移動至
和
,且
。
第一個旋轉描述了基底向量 和
之間的線性組合關係:
或寫成矩陣形式
。
按同樣的方式,第二次旋轉和第三次旋轉給出下列關係:
以及
。
合併以上結果即得旋轉座標系統的複合旋轉
。
每一個三維空間旋轉矩陣皆可用 Z-X-Z 為轉軸的歐拉角公式表示:
,
其中 和
分別代表
和
。
考慮反向問題:給定一個 階旋轉矩陣
,求出以 Z-X-Z 為轉軸的歐拉角
。因為
且
,可得
。除非設定轉角的範圍,代表連續旋轉的歐拉角並不是唯一的。設
,
其中 的計算採用
,傳回值的範圍是
,定義如下[1]:
這裡 是標準反正切函數,傳回值的範圍是
。若
,立刻有
。
若 ,則有無限多組解,一個特解為
,
。
除了上述以 Z-X-Z 為轉軸,我們也可以選擇其他軸作為轉軸,例如,以 Z-Y-X 為轉軸的旋轉方式稱為 yaw-pitch-roll:
- 以
為轉軸,轉角為
,稱為 yaw。
- 以
為轉軸,轉角為
,稱為 pitch。
- 以
為轉軸,轉角為
,稱為 roll。
yaw-pitch-roll 旋轉矩陣為 。事實上,只要連續兩個轉軸不相同便可產生合法的旋轉矩陣,共計有 12 種可能:
X-Y-X Y-X-Y Z-X-Z
X-Z-X Y-Z-Y Z-Y-Z
X-Y-Z Y-Z-X Z-X-Y
X-Z-Y Y-X-Z Z-Y-X
在代數中,所有的行列式等於 的正交矩陣構成一個群 (group)。三維空間的旋轉矩陣形成的群稱為特殊正交群 (special orthogonal group),記作
。對於任意
階旋轉矩陣
且
,請讀者自行證明下列性質:
,即旋轉不改變向量長度 (保長映射,說明
的特徵值的絕對值為
)。
,即旋轉不改變兩點的距離。
,即旋轉保留向量內積,故不改變兩向量之間的夾角 (保角映射)。
,即旋轉保留向量外積。
註解
[1] 維基百科:atan2



根據 http://blog.sina.com.cn/s/blog_5fb3f125010100hp.html 說到
“旋轉向量的長度(模)表示繞軸逆時針旋轉的角度(弧度)。旋轉向量與旋轉矩陣可以通過羅德里格斯(Rodrigues)變換進行轉換。”
請問
1.某一旋轉向量為 [ 0,0,0],是否代表沒有旋轉?
2.可以舉幾個簡單的例子來說明旋轉向量嗎?
例如
a.某一旋轉(原點不變)為 只繞X軸正30度旋轉,他的旋轉向量=[?,?,?]
b.某一旋轉(原點不變)為 只繞Y軸正45度旋轉,他的旋轉向量=[?,?,?]
c.某一旋轉(原點不變)為 只繞Z軸正90度旋轉,他的旋轉向量=[?,?,?]
_
上文羅德里格旋轉公式(Rodrigues’ rotation formula)已經給出了旋轉矩陣 公式,
公式,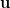 是轉軸所指的單位向量,
是轉軸所指的單位向量, 是旋轉角。若X軸正30度旋轉,則轉軸為
是旋轉角。若X軸正30度旋轉,則轉軸為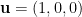 ,轉角為
,轉角為 ,代入公式即可算出旋轉矩陣。如果非要令
,代入公式即可算出旋轉矩陣。如果非要令 ,恕我亦無計可施。
,恕我亦無計可施。
謝謝您的回答。
聽您的回答 我問的旋轉向量 跟你指的 u 似乎是不一樣的東西?!
根據 1.維基百科 的 旋轉向量 http://zh.wikipedia.org/wiki/%E5%AE%9A%E5%90%91_(%E5%B9%BE%E4%BD%95)#.E6.97.8B.E8.BD.89.E5.90.91.E9.87.8F
“他新創了一個向量方法來描述任何轉動;轉動的轉動軸與向量同線,向量的量值就是轉動角度,稱此向量為旋轉向量”
2. http://blog.sina.com.cn/s/blog_5fb3f125010100hp.html
我所認知是
“旋轉向量r(是個3個維度的向量),可以透過Rodrigues轉換成旋轉矩陣R(3×3),
可再藉由R得出個別繞三軸旋轉的角度。”
1.請問我的認知是否正確?
2.上面”轉動的轉動軸與向量同線”,是什麼意思可否舉例說明?
2.可否舉幾個簡單的實例,來說明旋轉向量。
再次感謝
若X軸正30度旋轉,則轉軸為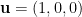 ,轉角為
,轉角為 ,維基百科所述的旋轉向量即為
,維基百科所述的旋轉向量即為 。旋轉向量僅能表達卻無法用於計算,四元數是更好的選擇:
。旋轉向量僅能表達卻無法用於計算,四元數是更好的選擇:
老師看了這篇講解,存在一個疑問。如果某個物理量是軸矢量,情況一:對它採用左旋參考系。對這個軸矢量進行旋轉變換(transform from left-hand laboratory frame to left-hand rotating frame)。情況二:對它採用右旋參考系。對這個軸矢量進行旋轉變換(transform from right-hand laboratory frame to right-hand rotating frame)。
這兩種情況,有什麼區別呢?
wiki說這是外代數的內容,然後就困惑了。
我是對磁矩進行旋轉變換,感覺左旋以及右旋的矢量,在進行矩陣運算的時候,並不應兩計算規則。
一直承蒙老師指點,十分感謝。
我不是很懂exterior product與bivector,請查閱下面連結的第二章:
Click to access Linear%20algebra%20via%20exterior%20product.pdf
老師,非常感謝您一直的指導,收到連接,開始閱讀。(ps:光速回覆的老師!!)
將 代入上式,立得
代入上式,立得  。如何知道
。如何知道  而不是
而不是 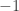 ?
? 且
且 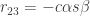 ,可得
,可得  “,
“, 一樣可取正負值? 怎麼知道
一樣可取正負值? 怎麼知道  而沒有負號??
而沒有負號??
同樣的,”因為
感謝指教!
已針對你的問題補充說明,請查閱。
請問老師如果我有問題是一旋轉後3×3的矩陣R=[n t b],那它相對於最一開始原始座標系x0,y0,z0分別轉多少度?因為如果我用歐拉角Z-Y-X為轉軸逆推,它會是由原始座標系方位先轉z,再由”轉完後”的座標系方位去轉y,之後”再次轉完後”的座標系方位去轉x,但如果我是要全部轉軸的方向都是原始座標系x0,y0,z0,那是要哪種堆導?
我不很確定你的問題,維基百科列出12種旋轉方式的旋轉矩陣 (R=[ntb])
https://en.wikipedia.org/wiki/Euler_angles#Rotation_matrix
挑選你要的旋轉方式,按照上文末的反向問題解法可解出三個轉角
https://en.wikipedia.org/wiki/Rotation_formalisms_in_three_dimensions#Conversion_formulae_between_formalisms
如果你的問題是關於extrinsic rotations,見下面的討論:
https://en.wikipedia.org/wiki/Euler_angles#Relationship_with_physical_motions
沒錯我的問題就是extrinsic rotations,感謝老師
老師您好,我建立了一個座標(F1),建立好後透過向量內積確定XYZ間皆為垂直。然後我對F1的Y軸旋轉”-30″度後產生一個新的座標系(F2),建立好建立好後透過向量內積確定XYZ間是否垂直,結果發現F2的XZ向量間的夾角變成了83.80度。想請問老師對此有何看法,謝謝
建立好建立好後透過向量內積確定XYZ間是否垂直 → 建立好後透過向量內積確定XYZ間是否垂直
我想到兩種可能:
1) 你發現了一套新幾何學;
2) 你算錯了。
老師好,
如果是座標點(1,0,0)以軸(X,Y,Z),X=Y=Z旋轉30度,要求該點的新座標。
請問也是用歐拉角公式來求嗎?
請用羅德里格旋轉公式計算,由 ,
, 可得旋轉矩陣。
可得旋轉矩陣。
請問老師,本頁歐拉角公式是旋轉座標系還是旋轉向量時使用?
根據wiki,兩者的旋轉矩陣的theta會差一個負號。
https://en.wikipedia.org/wiki/Rotation_matrix#cite_note-3
本頁看敘述應是旋轉座標系,wiki則是旋轉向量,但兩者的旋轉矩陣卻相同
本文的歐拉角公式給出的是旋轉矩陣,新座標系是舊座標系經旋轉而得。
請問一下,
有一原始座標(x0,y0,z0),目的為座標(x1,y1,z1),
要如何求得其旋轉矩陣。
這應該有無限多組解欸