設 
查詢特徵分析相關文章：
特徵值與特徵向量的意義與基本性質：
- 答Rich──關於特徵值與特徵向量的物理意義
- 自由振動系統的特徵值與特徵向量
- 特徵向量是甚麼物，恁麼來？
- 從不變子空間切入特徵值問題
- 特徵值的代數重數與幾何重數
- 幾何重數不大於代數重數的證明
- 相異特徵值對應線性獨立的特徵向量之簡易證明
- 特徵多項式蘊藏的訊息
- 左特徵向量與右特徵向量
- 廣義特徵值問題
- 拒絕行列式的特徵分析
特徵值與特徵向量的計算與化簡方法：
- 利用高斯消去法計算特徵值與特徵向量
- 不使用行列式的特徵值和特徵向量算法 (上)
- Krylov 子空間法
- 利用循環子空間計算特徵多項式
- 不可逆矩陣的特徵多項式
- Wielandt 緊縮──保特徵值的矩陣降階法
- 分塊矩陣特徵值的計算方法
- 肉眼判讀特徵向量
- 實對稱矩陣特徵值和特徵向量的探索解法
- 限定算子的特徵值與特徵向量 (上)
一般性質
逆矩陣
特徵值：
特徵向量：
冪矩陣
特徵值：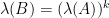
特徵向量：，但若 
，
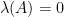的幾何重數會隨 
增大至代數重數。
，但若 ， 的幾何重數會隨 增大至代數重數。平移
特徵值：
特徵向量：
矩陣多項式
特徵值：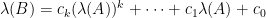
特徵向量：
矩陣指數
特徵值：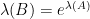
特徵向量：
矩陣函數
特徵值：
特徵向量：
相似
特徵值：
特徵向量：
特殊矩陣
秩一(rank-one)矩陣
(實矩陣 
)特徵值：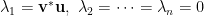
特徵向量：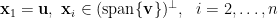
平面旋轉矩陣
![A=\left[\!\!\begin{array}{cr} \cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=A%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D+%5Ccos%5Ctheta%26-%5Csin%5Ctheta%5C%5C+%5Csin%5Ctheta%26%5Ccos%5Ctheta+%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
特徵值：
特徵向量：![\mathbf{x}_1=\begin{bmatrix} 1\\ i \end{bmatrix},~\mathbf{x}_2=\left[\!\!\begin{array}{r} 1\\ -i \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=%5Cmathbf%7Bx%7D_1%3D%5Cbegin%7Bbmatrix%7D+1%5C%5C+i+%5Cend%7Bbmatrix%7D%2C%7E%5Cmathbf%7Bx%7D_2%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Br%7D+1%5C%5C+-i+%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
正規(normal)矩陣
特徵值：未定
特徵向量：彼此正交 
常見的正規矩陣包括：Hermitian 矩陣/實對稱矩陣，skew-Hermitian 矩陣/反對稱矩陣，正定矩陣，么正矩陣/正交矩陣。
Hermitian 矩陣/實對稱矩陣
(實矩陣 
)特徵值：實數
特徵向量： (實矩陣 
)
(實矩陣 )skew-Hermitian 矩陣/反對稱矩陣
(實矩陣 
)特徵值：純虛數
特徵向量：
正定(positive definite)矩陣
對於任一非零向量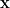 
，
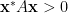。複正定矩陣隱含 Hermitian，實正定矩陣隱含對稱。
，。複正定矩陣隱含 Hermitian，實正定矩陣隱含對稱。特徵值：正數
特徵向量： (實矩陣 
)
(實矩陣 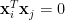)Gramian 矩陣
(實矩陣 
)，
是 
階。 是一半正定矩陣。特徵值：非負數
特徵向量： (實矩陣 )
(實矩陣 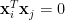)么正(unitary)矩陣/正交(orthogonal)矩陣
(實矩陣 
)特徵值：
特徵向量： (實矩陣 )
(實矩陣 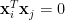)冪零(nilpotent)矩陣
存在正整數 使得 
。
使得 。特徵值：
特徵向量：
冪等(idempotent)矩陣
特徵值： 或 
或 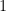特徵向量：對應特徵值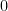 
的特徵向量屬於零空間 
，對應特徵值 的特徵向量屬於行空間 
。
的特徵向量屬於零空間 ，對應特徵值 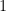的特徵向量屬於行空間 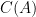。對合(involutory)矩陣
特徵值：
或 
或 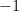特徵向量：對應特徵值 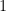的特徵向量屬於行空間 
，對應特徵值 的特徵向量屬於行空間 
。
的特徵向量屬於行空間 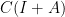，對應特徵值 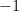的特徵向量屬於行空間 。Householder 矩陣(基本鏡射矩陣)
，其中 
。特徵值：
，
，特徵向量：
排列(permutation)矩陣
的每一行和每一列恰有一個元為 ，其餘元為 。 是一正交矩陣。特徵值：
特徵向量：
組合(combinatorial)矩陣
，其中 
。特徵值：
，
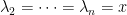
，特徵向量：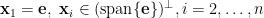
基本循環(circulant)矩陣
例：
特徵值：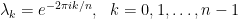
特徵向量：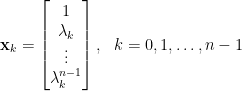
三對角(tridiagonal)矩陣
例：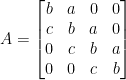
特徵值：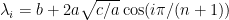
特徵向量：
相伴(companion)矩陣
例：
特徵值： 是多項式 
的根
是多項式 的根特徵向量：
馬可夫(Markov)矩陣(隨機矩陣)
特徵值：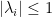
且 
且 特徵向量：對應特徵值 
的特徵向量的各個元皆大於或等於零。
的特徵向量的各個元皆大於或等於零。
線代啟示錄 