[2008年]十月初,哈佛大學一項學生學習成效調查結果,在哈佛教授間投下了一顆震撼彈。哈佛大學伯克教學中心 (Derek Bok Center for Teaching and Learning) 針對二十門課的教授、四百位學生,分別調查老師與學生是否掌握課堂「核心概念」(big idea)?跌破教授眼鏡的是,只有不到三成的學生,抓到教授在那門課想傳達的核心概念。…… 哈佛發現,即便是聰明又會考試的全美資優生,也經常帶著偏見的知識前來學習。他們很會考試但不會問好問題,他們習慣被動學習,導致學習成效很差。在一個知識持續變動的時代,哈佛意識到,「如何教」比「教什麼」更重要;他們更提醒全世界各級老師與父母,在學習這條路上,角色必須調整,我們不再是單向傳遞知識的聖人 (sage),而是與學生一同探索學習的伙伴 (collaborator)。
───〈哈佛的難題〉,《校園天下》
(更新修訂中,日後將予以分類)
線性代數有甚麼學習改進方法?
線性代數與微分方程都有特徵多項式,這兩門學科有甚麼關係?
線性變換與矩陣有甚麼關係?
矩陣乘法的定義從何而來?二矩陣相乘代表甚麼意義?
矩陣乘法有哪些計算方式?
矩陣代數有哪些運算規則與技巧?
我知道 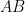 不一定等於
不一定等於  ,但
,但 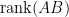 是否等於
是否等於  ?
?
我知道 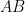 不一定等於
不一定等於  ,但它們是否擁有甚麼相同的性質?
,但它們是否擁有甚麼相同的性質?
若  和
和 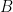 是
是 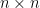 階矩陣,為甚麼
階矩陣,為甚麼  可以推論
可以推論  ?
?
線性代數的核心概念是甚麼?我能夠從一個 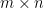 階矩陣
階矩陣  獲得哪些重要的訊息?
獲得哪些重要的訊息?
向量空間有向量加法和純量乘法,但為甚麼沒有「向量乘法」(不是內積) 運算?
為甚麼線性組合 (向量加法與純量乘法) 是向量空間的基本運算?
為甚麼向量空間不稱作「向量集合」?子空間和向量空間又有甚麼關係?
線性方程 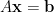 的解有甚麼幾何意義?
的解有甚麼幾何意義?
為甚麼齊次方程  的解集合構成子空間 (零空間),但線性方程
的解集合構成子空間 (零空間),但線性方程 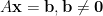 的解集合卻不是子空間?
的解集合卻不是子空間?
為甚麼線性方程的通解 (general solution) 可以表示成特解 (particular solution) 和齊次解 (homogeneous solution) 之和?特解是唯一存在嗎?
為甚麼不可逆矩陣又稱為奇異 (singular) 矩陣?
怎麼證明上三角矩陣的逆矩陣也是上三角矩陣?有沒有別於直接計算的證法?
我知道 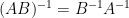 ,
, 有簡單的計算公式嗎?
有簡單的計算公式嗎?
為甚麼多項式  也稱為向量?
也稱為向量?
線性映射與座標變換有甚麼不同?
為甚麼 ![\left[\!\!\begin{array}{cr} a&-b\\ b&a \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D+a%26-b%5C%5C+b%26a+%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002) 可以用來表示複數
可以用來表示複數  ?
?
為甚麼三維空間變換要用  階矩陣表示?
階矩陣表示?
為甚麼矩陣秩代表矩陣的「真實尺寸」?
矩陣  ,
, ,
, ,
, ,
,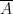 和
和  有相同的矩陣秩嗎?
有相同的矩陣秩嗎?
為甚麼基底必須由一組線性獨立向量組成?
為甚麼矩陣的行空間就是線性變換的值域?零空間就是線性變換的核?
基本列運算為甚麼不改變矩陣的行向量的線性組合關係?
為甚麼  的行空間包含
的行空間包含 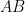 的行空間?為甚麼
的行空間?為甚麼 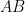 的零空間包含
的零空間包含 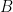 的零空間?有沒有較為直覺的解釋?
的零空間?有沒有較為直覺的解釋?
從計算結果來看,簡約列梯形式 (reduced row echelon form) 似乎是唯一存在的,但如何證明呢?
矩陣  與其轉置矩陣
與其轉置矩陣  的關係有甚麼幾何解釋?
的關係有甚麼幾何解釋?
Jacobian 矩陣和 Hessian 矩陣有甚麼關係?
矩陣  與其伴隨矩陣
與其伴隨矩陣 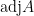 有甚麼關係?
有甚麼關係?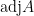 的伴隨矩陣又是甚麼?
的伴隨矩陣又是甚麼?
行列式有甚麼直覺解釋?
行列式有甚麼幾何意義?
變換矩陣的行列式有甚麼物理意義?
二矩陣和的行列式  有計算公式嗎?
有計算公式嗎?
行列式  與
與  的行向量之間存在甚麼不等關係嗎?
的行向量之間存在甚麼不等關係嗎?
為甚麼要定義向量內積?甚麼是內積空間?
我知道 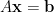 代表聯立方程組,但為甚麼會有特徵方程
代表聯立方程組,但為甚麼會有特徵方程  ?
?
線性變換的特徵值與特徵向量有甚麼幾何 (物理) 意義?
為甚麼任一方陣必存在至少一特徵值?
- 拒絕行列式的特徵分析 (定理一)
為甚麼相異特徵值的特徵向量是線性獨立的?
為甚麼特徵值的幾何重數不大於代數重數?
如果不使用 Cayley-Hamilton 定理,如何確認對於 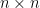 階矩陣
階矩陣  ,必定存在
,必定存在  次多項式
次多項式 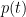 使得
使得 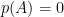 ?
?
- 拒絕行列式的特徵分析 (定理一)
我知道正定矩陣的定義,但是否有較富直覺的解釋?
實對稱矩陣和 Hermitian 矩陣有哪些應用範疇?
哪些是我應該知道的重要矩陣分解式?
奇異值分解有甚麼幾何意義?
